遗传算法及基于该算法的典型问题的求解实践

阐明

遗传算法是一种非常有用的工具，可以帮助我们解决生活和科学研究中的许多问题。最近，当我查看与Beam Forming相关的内容时，我了解到该算法可用于优化阵列元素激发以降低侧叶。因此，我专门学习并了解了这种算法。我发现它很有趣，所以我在过去两天中了解了这种算法，并了解了这一算法。实践内容总结为博客文章。

遗传算法的核心思想/步骤在于迭代。这篇博客文章是第一次写（2024.3.15），仅包括一些对算法的基本和必要概念的介绍，以及两个相关应用程序的实践，稍后还有更多相关的应用程序（例如横向成式优化），我将不时迭代博客文章，以积累和理解细节。

博客

20240315我第一次写博客

内容1。遗传算法的概述1.1遗传算法的来源和应用领域

Baidu百科全书的引言非常广泛，但也有很多有用的信息：遗传算法（GA）是由美国的约翰·霍兰德（John Holland）在1970年代首次提出的。该算法是根据自然界生物的进化定律设计和提出的。的。它是一个计算模型，可模拟达尔文生物进化论的自然选择和遗传机制。这是一种通过模拟自然演化过程来搜索最佳解决方案的方法。该算法使用数学方法将问题解决过程转换为类似于生物进化中染色体基因的相交和突变的过程。在解决更复杂的组合优化问题时，通常可以比某些常规优化算法更快地获得更好的优化结果。遗传算法已被广泛用于组合优化，机器学习，信号处理，自适应控制和人工生命等领域。

1.2与遗传算法有关的基本名词概念

要了解该算法，我们必须首先从与之相关的基本概念开始。在随后的应用程序实践中，我将在数学建模和应用程序问题的解决方案过程中一一将这些概念与一一相关。参考文献[1]中的这些概念的引入很棒，本节主要是指此信息。

1。基因和染色体

在解决各种应用程序问题时，我们首先需要映射我们要解决的问题，即数学建模！数学问题的可行解决方案称为“染色体”。可行的解决方案可以由多个元素（多个变量）组成，并且该溶液的每个元素（变量）称为“染色体上的基因”。 ”。

2。健身

我认为遗传算法解决问题的本质是通过连续迭代来接近最佳解决方案的过程。我们将产生许多染色体（可行解决方案）。那么，我们如何衡量这些染色体的利弊？在遗传算法中，我们使用健身来测量每个染色体的利弊。我们构建一个适应性函数，以“评分”每种迭代中生成的所有染色体，以获得每个染色体的适应性。在随后的加工过程中，我们可以消除适合度较低的染色体，并且仅保留具有较高适合度的染色体，从而使染色体的质量更好，更好地迭代后。 [与达尔文的进化论类似，某些人无法适应环境（相当于在这里适应低的某些染色体）。

3。交叉

假设将在每次迭代中生成N染色体，则相交用于解决如何生成新染色体的问题：交点的过程需要随机从上一代中随机搜索两个染色体，然后通过某些染色体产生了两个染色体。算法。染色体（例如单点交叉，双点交叉，顺序交叉等等再次提出），还有另一个问题：如何选择这两个染色体？在上一步的适应性评估中，我们计算了每个染色体的适应性。越过时，我们将根据适应性概率（由轮盘等算法选择）选择更高的健身开yunapp体育官网入口下载手机版，越过染色体。适应性概率的计算：染色体I的适应性概率（被选中的概率）=染色体I /所有染色体适应性之和的适应性。

4。突变

越过时，我们更喜欢具有高健身的染色体，因此我们可以确保每个进化都可以留下出色的基因，但是它只能选择原始结果集，并且仍然有几个基因，但是它们已交换。组合顺序（只能确保n个进化后，计算结果都更接近局部最佳解决方案，并且可能永远无法实现全局最佳解决方案。为了解决这个问题，我们需要引入突变。突变方法：对于上述交叉过程产生的染色体，我们可以适当（这是一个称为突变速率的参数设置问题：如果每个交叉后突变染色体实际上很难收敛，因此选择了其中有多少人是选择的突变。条形是一个需要考虑的问题。以及反变形突变，开关突变等。同样，参考材料中有更多详细的描述[2]。染色体（或基因的顺序已更改，破坏了当前的搜索限制，并且更有利于找到全局最佳解决方案的算法。

5。复制

在每种演化中，为了保留上一代的出色染色体，上一代中具有较高适合度的几个染色体需要直接复制到下一代完整。假设需要为每个演化生成N染色体，则需要通过横截面生成NM染色体，并且通过复制上一代中适应最高的M染色体来生成其余的M染色体。

6。大约迭代结束

在基于遗传算法解决各种问题时，我们应该在结束之前迭代多少次？通常有两种方法可以确定迭代何时结束：一种是预设迭代次数。在某些实际应用中，可以预先计算获得更好的结果时的进化数量。例如，您通过许多实验发现，无论输入数据如何变化，算法都可以在Evolution K Times之后获得最佳解决方案，因此您可以将演变数设置为K。但是，实际情况通常是并非如此理想，因为当获得最佳解决方案时，不同的初始输入会导致截然不同的迭代。第二个是限制精度范围。如果该算法想实现全球最佳解决方案，则可能必须经历许多演变，这将极大地影响系统的性能。然后，我们可以在算法的准确性和系统效率之间找到平衡。我们设置了一系列可以预先收到的结果。当算法经历K演变时，一旦发现当前的结果在误差范围内，它就会终止算法。但是，此方法还具有其缺点：在某些情况下，它可能会在几次演变后输入错误范围，但是在某些情况下，进入错误允许范围可能需要很多很多次。这种不确定性使算法的执行效率无法控制。

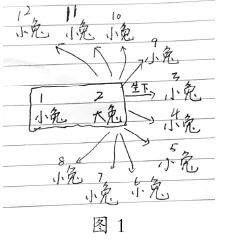
2。基于遗传算法解决各种问题的基本思想和过程

上一篇文章解释了可能与遗传算法有关的参数及其用途（在算法中的作用）。序列化这些概念构成了典型的遗传算法处理过程。

对于各种应用程序问题，首先要做的就是澄清问题并执行数学建模。

然后预设参数：例如，我们需要预设多少个染色体，我们必须预设多少迭代，我们有多少可变性率，以及我们需要直接从父母那里复制多少个染色体？

然后，基于数学建模的结果，响应此应用问题，染色体是初始化的，并且适应性功能旨在计算这些初始化的染色体的适应性和选择概率。

然后，您可以输入迭代循环：交叉---->突变---->复制---->交叉--->突变--->复制...直到达到预设的迭代数量，或其他预设迭代是满足的终止条件。

典型的遗传算法过程如下：

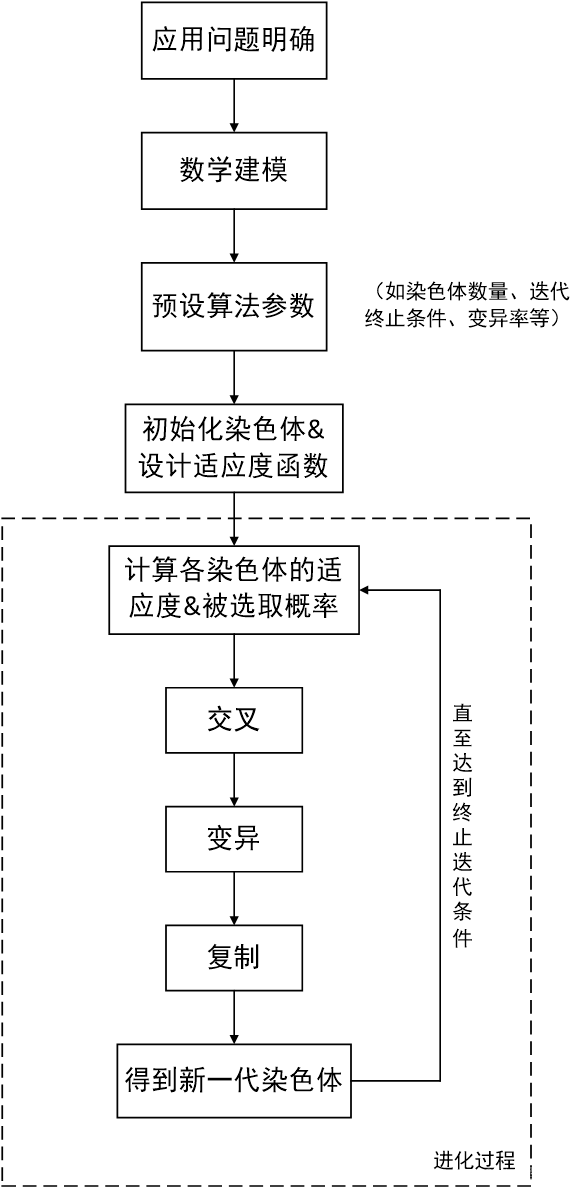
图2.1典型的遗传算法流程图

在本章和上一章的指导下，我们可以尝试将此算法部署到各种应用程序问题。

3。根据遗传算法解决调度问题3.1问题描述

假设有N任务，并且需要将负载平衡器（您）分配给M服务器节点进行处理。每个任务的任务长度（任务数量）和每个服务器节点的处理速度是已知的。请提供一个任务分配方法，以最大程度地减少所有任务的总处理时间。 [类似于服务器调度类似的各种问题的答案]

3.2问题建模和参数预设

问题建模：（调度问题的建模相对简单），假设我们知道问题中每个任务的长度是：task = [任务（1），任务（2），…task（n）]，...每个节点的处理速度为：nodes = [node（1），节点（2），…node（m）]。我们可以在每个任务和每个节点之间构造相应的处理时间矩阵：

（3-1）

指示将第i-thes任务交给处理J-th节点的时间。

初始化染色体：我们将初始染色体编号（或通常称为初始种群编号）预设给K，因为每个染色体都对应于可行的溶液，因此很容易理解每​​个染色体是长度的一维载体n：a = [a（1），a（2），…a（n）]，向量中的每个元素a（n）对应于一个基因，其物理含义是我们将nth任务分配给a （n）服务器节点。我们可以基于随机分配方法来完成K染色体的初始化。目前，我们可以获得与染色体相对应的矩阵，其大小为：k*n。

设计健身功能：健身是我们用来评估每个染色体的利弊的指标。在这个问题中，很容易认为可以使用与每个染色体相对应的任务分配中花费的总时间来构建健身功能：

右边（k）= max（节点1花费时间，节点2花费时间，...节点M需要时间）（3-2）

我们找到了K染色体完成任务所需的时间（我们可以在解决方案期间从前一个timematrix矩阵找到时间），最后我们可以获得长度k的一维向量：右边（2），…右边（k）]，向量中的每个值对应于与K-th染色体相对应的任务分配下完成任务的时间。应当指出的是，在此任务中，所花费的时间越少，相应的任务分配（染色体）越好，并且其适合度越高，因此我们可以在这里取出总时间来获得每个染色体的适应性：

适应性= 1./timeneed（3-3）

获得适应性后，更容易找到越过时选择每个染色体的概率：

SelectionProbability = Adaptability（K）/（SUM（ADAPTIABIE））（3-4）

完成上述准备工作后，我们可以输入迭代部分。在以下几种申请实践中，我将不再以如此详细的方式解释这一部分。

3.3解释解决方案过程中的几个核心代码模块3.3.1如何找到父母的染色体

在进行跨界之前，您需要从上一代的父母和母亲的两个染色体中找到。在第1.2节中，该过程描述如下：“我们更喜欢根据适应性概率（通过轮盘等算法选择）越过更高适合度的染色体。”适应性概率（被选为概率的计算方法），本节介绍了如何根据轮盘算法选择父母的染色体。代码块如下：

图3.1轮盘算法功能

该算法的基本原理实际上非常简单：首先在[0 1]中随机生成概率值randval，然后遍历并累积与先前获得的染色体相对应的概率阵列。当累积的概率在KTH结果下：（ selection -probibility（1）+ selection -probability（2）+…selectionprobability（k））≥Randval时，选择了与K相对应的染色体。此功能的调用模块代码如下：

图3.2轮盘算法的调用模块（选择父和父染色体）

染色体对应于上一代染色体阵列。为了确保两次选择两次，判决模块已添加到代码中。

轮盘算法是选择父染色体的一种简单且经典的方法。当然，可能还有其他方法。简而言之，这些方法的主要目的是优先选择具有高概率的父染色体（高健身），但不是损失随机性。

3.3.2如何交叉

找到父母的染色体实际上是交叉路口的一部分。本节讨论了以下步骤：如何在获得父母的染色体后如何产生新的染色体？在第1.2节中，该过程描述如下：“交叉过程需要随机搜索上一代中的两个染色体，然后使用一些算法来生成新的染色体（例如单点交叉和双点交叉）。 ，顺序交叉等。不同的应用程序场景可能使用不同的跨界算法。”

在本章讨论的调度问题中，我们不需要考虑每个基因的唯一性：可以重复基因，或者可以将不同的任务分配给同一服务器节点。 （但是，可能不是其他申请问题，例如在以后的章节中将讨论的旅行经销商问题）。无需考虑每个基因的唯一性，可以使我们在这里设计跨音估时选择更多。这次，我在代码中使用了最简单的单点交叉方法：

图3.3单点交叉算法模块

实现非常简单：我们随机选择一个任务点，然后将母体染色体的一部分放在节点前的子染色体上，然后将母体染色体的一部分放在子染色体的节点后面开元ky888棋牌官方版，我们，我们可以获得（生成）剪接的剪接新染色体。

3.3.3如何互化

第1.2节中变体部分的描述如下：“突变方法：对于上述交叉过程产生的染色体，我们可以适当（这是一个称为突变率的参数设置问题：如果每个交叉后进行染色体，则进行了变化。实际上很难收敛，因此选择其中有多少是一个需要考虑的问题。有很多，例如：位置翻转突变，交换突变，逆转突变，开关突变等”。

同样，调度问题也不考虑每个基因的非重复性问题，因此方法选择更加灵活。这次，我随机选择了突变代码中的一个基因：

图3.4突变模块代码

在该代码中，Mutenum对应于我们需要以预设突变率突变的染色体数量。 Staynum表示我们需要从上一代复制多少染色体，而这些染色体不参与突变。然后，我们从新生成的染色体中选择染色体，然后随机选择其基因之一将其变成另一个随机基因。

3.4解决结果

在此模拟中，预设了10个任务和5个服务器节点。每个任务的长度是在[1 20]中随机生成的，每个服务器节点节点的速度是在[1 10]中随机生成的。假设染色体的数量为100，预设的变异率为0.02，预设的迭代次数为100，并且每次直接从上一代直接复制的染色体数量。

获得的仿真结果如下：

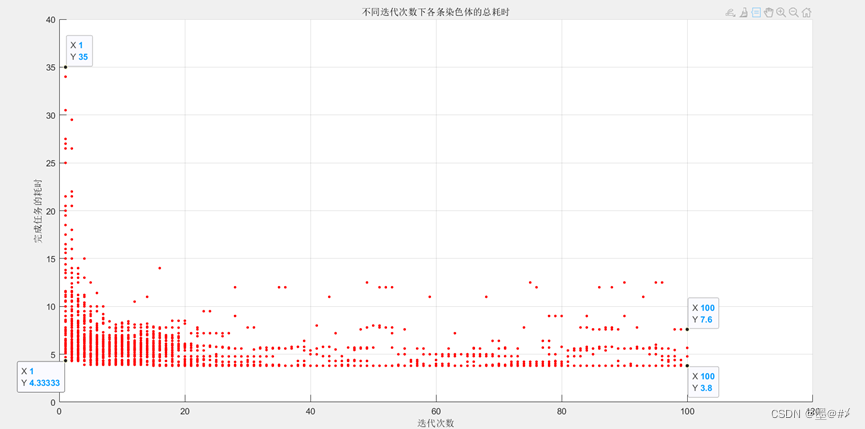
图3.5每次迭代中每个染色体的时间消耗

如果我们选择每次迭代结果的染色体所需的时间最少，那么我们实际上可以看到，大约8个迭代后，已经有一些染色体需要最终时间到3.8。

3.5摘要和思想

根据第2章中给出的算法过程的指导，本章完成了基于遗传算法和某些算法模块的细节解决调度问题的模拟实践。在遗传算法的应用领域中，调度问题相对简单，用作介绍性，并在更合适的方向上熟悉该算法。我希望本章的工作内容对读者有帮助。

另外，在解决此问题的过程中，实际上有许多细节要考虑：例如，1。可以将多少变化率设置为更快地完成迭代？ 2。如果在突变过程中多个突变点，它会加速迭代吗？ 3。在交叉路口选择父染色体时，如果我们仅从概率较低的（K-Staynum）染色体中进行选择（因为我们将直接将先前的Staynum染色体复制到下一代），那么对迭代会有什么影响？ 4。还有其他更好的父染色体选择算法和横截面算法吗？等。这些问题是有趣的研究方向。

4。根据遗传算法解决旅行业务问题

考虑到我在第3章中提供了许多详细信息，并且基于了解第3章的调度问题的后续应用程序问题应该更容易理解，因此第4章和将来可能会添加的各种应用程序。在问题的实践中，我将主要介绍关键点和差异。

4.1问题描述

旅行经销商的问题是一个非常经典的问题（对我来说，在与遗传算法接触之前，我已经了解了这一点）。这个问题的描述很简单：旅行推销员问题（旅行推销员问题，也称为小贩的负担问题）：鉴于一系列城市与每个城市之间的距离，请找到一次访问每个城市的解决方案，然后返回到开始的最短循环。 [在基于遗传算法解决此问题时，我们需要始终关注它：每个城市只能访问一次！这是给出的

4.2问题建模和参数预设

问题建模：众所周知，我们有n个城市，每个城市cityx的坐标= [cityx（1），cityx（2），…cityx（n）]，cityy = [Cityy（1），Cityy（2）， …Citey（n）]。我们可以在两个城市之间构建相对距离矩阵：

（4-1）

它表明第i-th城市与J-th城市之间的相对距离。该矩阵的大小为n*n。

初始化染色体：我们将初始染色体编号（或通常称为初始种群编号）预设给K，因为每个染色体都对应于可行的溶液，因此很容易理解每​​个染色体是长度的一维载体n：a = [a（1），a（2），…a（n）]，向量a（n）中的每个元素都对应于一个基因，其物理含义是我们的旅行者在第n期参观的城市。我们可以基于随机分配方法来完成K染色体的初始化。目前，我们可以获得与染色体相对应的矩阵，其大小为：k*n。但是，应该注意的是，每个染色体中的每个基因都有独特性！

设计健身函数：在这个问题中，很容易认为可以使用与每个染色体相对应的总距离来构建健身功能：

rangesum（k）=总和（从城市1到城市2 +城市2到城市3 +… +从城市n到城市1的距离）（4-2）

我们找到K染色体所需的总距离时间（在解决方案过程中，我们可以找到与先前的distancematrix矩阵的相对距离），最后我们可以获得长度k的一维矢量：distancesum = [distancesum = [distancesum（1） ，距离（2），…距离（k）]，矢量中的每个值对应于k-th染色体所取的总距离。应该注意的是，在此任务中，距离越短，任务分配（染色体）越好，其适合度就越高，因此我们可以在这里计算总距离以获得每个染色体的适应性：

适应性=1。/距离（4-3）

获得适应性后，更容易找到越过时选择每个染色体的概率：

SelectionProbability = Adaptability（K）/（SUM（ADAPTIABIE））（4-4）

完成上述准备工作后，我们可以输入迭代部分。

4.3解释解决方案过程中的几个核心代码模块4.3.1如何交叉

旅行者问题与以前的调度问题之间的一个主要区别是，旅行者下染色体的每个基因都不同。因此，在以前的第3.3.2节中使用单点交叉无法实现：因为不能保证父母染色体前的基因与父染色体后面的基因之间没有重复。在此代码中，我选择了顺序的横截面算法来实现：

图4.1连续交叉的实现

在这里实现交集的想法是：首先，我们随机找到一个相交点，然后我们将父染色体交点前的所有基因分配为儿童染色体。对于儿童染色体相交的基因的基因，我们横穿母体染色体，如果发现一个基因在亚染色体中没有基因，请在亚染色体后面附着基因直至亚染色体的长度直至亚染色体的长度是N。

4.3.2如何互化

同样的原因是：在旅行者问题下染色体不同。对于这里的突变，我们随机选择两个基因进行位置交换以完成突变。

图4.2突变算法模块

Mutenum是根据预设突变率获得的突变染色体的数量。该模块非常简单：随机选择染色体，随机选择两个具有不同染色体的基因进行交换。

4.4解决结果

在此模拟中，预设了10个城市，每个城市的水平和垂直坐标是在[1 100]内随机产生的，有10个染色体预设，可变性率为0.02，100次迭代预设，预设了2个染色体的数量每次直接从上一代复制。

获得的仿真结果如下：

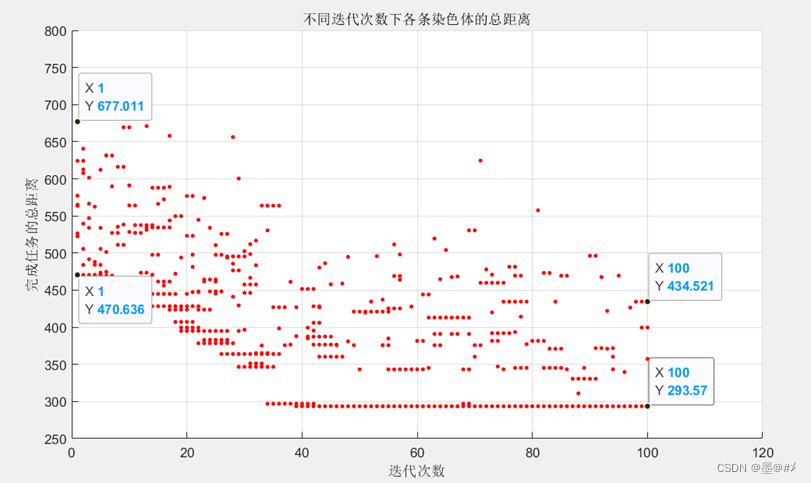
图4.3不同迭代下每个染色体下的总距离

可以看出，随着迭代次数的增加，与每次生成的染色体相对应的总距离正在向下移动。此外，我选择了与初始化期间最近染色体相对应的路径，以及100个迭代后开yun体育app入口登录，如下所示：

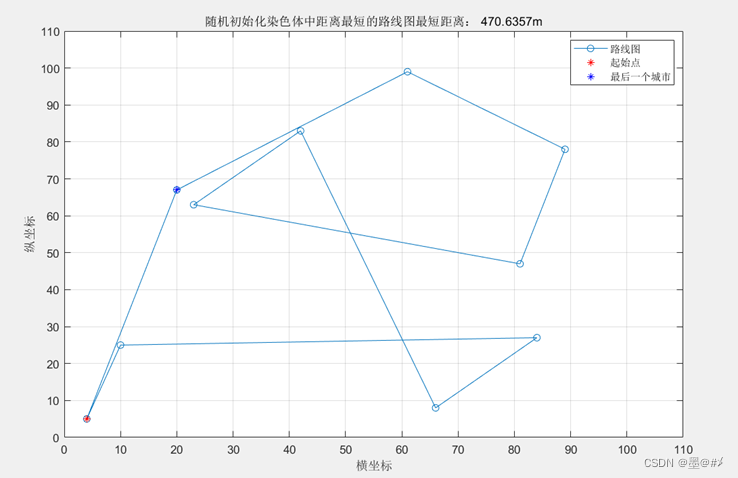
图4.4初始化染色体中总距离最短的路径选择

图4.5选择100次迭代后生成的染色体中总距离最短的路径选择

4.5摘要和思想

本章使用遗传算法来解决旅行商商问题，并分析某些算法模块的细节。旅行商人问题是一个经典的组合优化问题，在操作研究和理论计算机科学中非常重要。我希望本章的工作内容对读者有帮助。

在第3.5节中，我在解决方案过程中提出了一些有趣的细节。还有两个：1。我们初始化的染色体数量对迭代的收敛速率有什么影响？ 2。我们设定的染色体数量的比率有多高，直接从上一代复制到整体演化效果？

V.其他申请问题

我最初想在此博客文章中根据遗传算法编写优化的波束形成，但是看来我在这里写了足够的内容。在随后基于遗传算法解决其他问题的练习中，我将以链接的形式将新写的博客文章附加到本章。

6。摘要

这篇博客文章提供了遗传算法的系统详细介绍：包括其相关概念，经典处理流等。使用调度问题和旅行经销商作为研究对象，我们探索了如何使用遗传算法来解决这两个问题（如截至时， 2024.3.15）。如上一个描述部分中所述：最近，当我查看与Beam Forming相关的内容时，我了解到该算法可用于优化数组元素激发以降低侧叶。我专门学习并学到了这种算法。我发现这很有趣，因此我将这两个Tian的内容放在了该算法的学习和实践上，并将其汇总到了博客文章中。我将不时补充信号处理，自动驾驶和人工智能中遗传算法的应用程序实践示例。

7。参考材料

[1]在10分钟内了解遗传算法（包括源代码）-Zhihu（Zhihu.com）

[2]遗传算法中的常见遗传算子-Zhihu（Zhihu.com）

8。代码参考

此博客文章的仿真代码如下（包括.m和.txt版本）：

基于此算法代码（MATLAB）资源对应于博客文章的遗传算法和典型问题的解决方案-CSDN库