学生感兴趣的才是最有价值的 ——“斐波那契数列”教学实录与评析

我们的梦

学生感兴趣的是最有价值的

“斐波那契序列”的教学记录和评估

我们的想法

庞大的数学大厅里有许多辉煌的珍珠，斐波那契序列是其中的一颗。这些知识是在人民教育出版社六年级第二卷的第65页的“阅读材料”单元中引入的。经过调查，我们发现，由于这些内容不是必需的测试范围，因此教师在教学过程中通常不会对此倍受关注。他们要么介绍一些句子，然后用中风描述。或要求学生一起阅读并匆忙结束；有些人只是将其用作作业，让学生回家阅读它。至于学生是否阅读，教师认为这是无关紧要的。很少有人认为教书是一个完整的课程。如何在教科书中使用“阅读材料”进行教学，以便成为学生可以知道，愿意知道和努力知道的亮点？在深入讨论之后，我们的工作室设计了斐波那契系列的课程示例，这些示例是由工作室里的英俊家伙王先生教授的。

教科书中斐波那契序列的引入分为四个部分：一个是兔子问题的完整表达；第二个是兔子问题的研究传奇。第三个是使用列表来表示研究结果；第四是使用序列来解释斐波那契序列是什么。最后问一个问题：您可以在斐波那契序列中找到规则吗？对于小学生来说，这种演讲方法似乎太合理和沉闷了，很难引起孩子们对探索的兴趣。

什么样的学习材料会让孩子感兴趣？ “学习的最佳动机是学生对学习材料本身感兴趣。”为了激发孩子们的兴趣，在课堂开始时，我们利用学生的爱情故事的本质来聆听故事，我们构成了一个短篇小说，例如“穷人的梦想富裕”。果然，老师生动的叙述吸引了孩子们，他们积极参与了“他真的可以赚钱？”的重大讨论。然后，老师指导学生从故事情况中提取有效的信息，然后通过合理的假设，一个有趣的生活问题巧妙地转化为数学问题。

了解兔子问题是本课程的关键部分。兔子问题的陈述有些晦涩而令人困惑。经过讨论，我们决定让学生两次自由阅读问题。阅读两次问题开元ky888棋牌官网版，孩子们在第一次“阅读”中大致知道问题是什么，在第二个“阅读”中独立思考，并对问题有个性化的理解。在阅读了两次问题之后，我们使用逐分分析来让孩子们在问题中表达对每个句子的解释。孩子们都很聪明。他们结合了自己的思想，并向他人的理解学习，并清楚地理解兔子问题的真正含义，从而消除了随后的独立操作和研究的障碍。

尽管这个问题已经清楚地理解了，但孩子们仍然对“第12个月可以有多少兔子”的问题感到困惑，并且不知道如何开始。这也是该课程的教学困难。该怎么办？

我们知道，建立数学概念的核心问题，数学定律的发现，数学问题的解决方案，甚至整个数学构建的构建在于培养和建立数学思想。数学思想有自己的特征和规则。他们没有反映在学生的理解或理解中。相反，它们必须通过学生的理解来获得他们自己的见解，并理解原则，法律和思维方法。

老师应该试图放弃孩子们可以自己探索的问题。老师应指导儿童无法及时解决的问题。兔子问题是一个全新的问题。当孩子们不知所措时，老师采取了决定性的行动，就好像他能够捡起它一样，并介绍了老子著名的话说：“世界上必须轻松地做的困难事情；世界上的大事情必须详细完成。”他组织了孩子们，以理解和理解老挝思想的深刻含义，并在此基础上指导孩子们使用转型思想，以找到研究兔子问题的最佳突破。最后，当老师和学生共同努力找到解决问题的规则时，老师有意义地叹了口气：难怪我说：“在世界上很难，必须以简单的方式完成。”这将使转变思想整合到整个探索过程中，并将它们扎根于孩子的年轻人，以便学生可以理解数学思想的真正含义。因为该课程不仅是为了获得12个月内有多少兔子的计算结果，而且更重要的是，让学生知道复杂的问题是通过多个增值的添加来由简单问题形成的。遇到如此复杂的问题时，您可以从最简单的问题开始，将困难变成简单，然后将复杂性变成简单性。解决数学问题是正确的，解决生活问题也是如此。

掌握了转型的数学思想之后，我们如何进行集体研究？是表格格式吗？还是使用真实的图片仿真方法？基于主要关注特定图像的小学生的思维特征，我们设计了成对的大兔子和小兔子配对的图片，并组织了孩子们一起操作，以详细说明操作过程中每对兔子的过去和现在，以便对兔子问题有更详细的了解。随着行动的加深，孩子们还突然意识到，他们从过去几个月中兔子对数变化的变化发现了规则。通过反思和验证，规则的正确性是一一确定的。当孩子们使用规则时，他们发现从第7、8个月到第12个月推断兔子的对数，甚至大声疾呼，甚至大声喊出了13个月和14个月的兔子对数，他们从混凝土形象的思维到抽象的逻辑思维中取得了质量的飞跃。

在这一点上，班级已经完成，孩子们已经理解并理解了斐波那契序列，并且基本上已经实现了教学目标，而且似乎我们可以在那里结束。但是，我们认为教学应该超越课堂本身的时间和空间的局限性，基于学生的终生发展，并指导学生从数学角度看待世界。因此，教师指导孩子们从分支机构的生长中找到斐波那契现象，从鹦鹉螺的美丽螺旋中找到斐波那契现象，并从日晒的种子的布置中找到斐波那契现象，从而使孩子们再次体验数学数学数学数学数学的过程。

卢Xun先生曾经说过：一个“红色豪宅的梦想”，学者们看到“变革之书”，道人看到欲望，才华横溢的男人看到挥之不去，革命者看到窃，谣言在宫殿里看到秘密！小数学家会从数学角度看待世界？他们看到了数学的美丽，数学的奇观，数学的奇观以及数学的无限魅力！

另外，让我们谈谈主题。在研究过程中，我们发现许多论文定义了斐波那契序列，如下所示：如果每个项目从第三项开始是前两个项的总和，则我们称之为fibonacci序列。序列中的每个数字称为斐波那契号。

我们搜索的相关信息提到：“观察trillium，野生玫瑰，南美血根，宇宙，凤凰，凤凰，凤凰，莉莉和蝴蝶的花瓣，我们可以发现他们的花瓣具有斐波那契数字：3，5，5，8，13，21 ... 34，有些是55或89，而其他花瓣很少，而这些花瓣数正是斐波那契系列中的“斐波那契数”。我们不能同意这些陈述。如果生活中的这些数字被标记为斐波那契数字，那么“一天不见彼此就像三个秋天一样”，“两个金莺在绿色的柳树中唱歌，一排乌格莱特在天空中”，“一只手有5个手有5个手指”并不全都被认为是fibonacci的荣誉吗？如果这些数字出现在斐波那契序列中，则在这种特定情况下，它们属于序列。一旦离开特定的序列，就无需给他们一个很难的名称，对吗？数学最好是现实！

课堂录音

教学目标：

1。通过操作和发现，总结了斐波那契序列的定律。

2。培养学生的问题审查能力和独立研究，观察和概括。

3。浸润和改变思想，体验数学与生活之间的紧密联系，并体验数学的美丽。

教学重点：了解兔子问题。

教学困难：发现并总结斐波那契序列的规则。

教学记录：

1.故事导入并提出问题

老师：学生，让我告诉你一个故事！曾几何时，有一个可怜的人梦想着整天富裕。有一天，他捡起了一对兔子，握住兔子并计划这样做：下个月，这对兔子将成长为大兔子，在另一个月，一对兔子可以在兔子长大时生下更多的兔子。一年后，我变得富有，有钱要盖房子，嫁给妻子，并有一个儿子！哈哈哈……

老师：学生，您认为他真的可以赚钱吗？

生命1：不，兔子可能会死。

老师：是的。

出生2：不，出生的兔子可能都是男性。

（孩子们都笑了）

老师（笑）：您有很多生物学知识，您确实需要有一个男性和女性。

学生3：您捡到的兔子应该退还给兔子的主人，否则所有者将非常焦虑。

老师：是的，当您拿起东西时，应该将其退还给原始所有者。这是成为人类的基本道德。

学生4：老师，我认为他会赚钱，因为兔子长大后可以生下一只小兔子。一只兔子长大后可以生下一点兔子。当他不断生下许多兔子时，他可以生下许多兔子。

老师：这很有意义。学生的演讲很棒！我们谈论的兔子繁殖问题只是一个生命问题。如果您对学生刚才提到的实际情况（例如兔子的死亡，兔子的性别）做出合理的假设，那么生命问题将转变为这样的数学问题：（提出了过程工具）假设一只新生的兔子可以在一个月内成长为一个大兔子，一个月可以在另一个月内出生一对兔子。此后，每月出生一只兔子，一年之内没有死亡。那么，第12个月将出生多少只兔子？

[评论]使用故事来提出生活问题会很快吸引学生的注意力。以及如何及时“恢复”生活问题并使它们成为数学？教练老师给了我们一个很好的例子。他只用几句话重新调整了他的公开思维，而数学问题从人生问题转变为出色的首次亮相。

2.通过句子分析句子并理解问题的含义

老师：请两次自由阅读此数学问题。 （学生阅读了问题）您是否完成了两次阅读？您如何理解这个数学问题？让我们一一谈谈。

学生5：这就是我理解第一句话的方式：“假设一对新生的兔子可以在一个月内成长为一只大兔子，而一对兔子可以在另一个月内生下一对兔子。”这意味着一对兔子可以在一个月内成长为一只大兔子，一个大兔子可以在另一个月内生下一对兔子。

老师：这个同学的单词非常使用！你听到了吗？兔子的单位是“正确的”开元棋官方正版下载，而一对兔子不仅是“”单位。谁会告诉我您对第一句话的理解？

第六代：这意味着在第二个月中，一对小兔子成长为大兔子，直到第三个月才能生下一对小兔子。

老师：是的！很清楚！

学生7：我理解以这种方式：在第一个月，有一对小兔子。到第二个月，这对兔子成长为一对大兔子。到第三个月，两只兔子生了一对小兔子。实际上，到了第三个月，有2对兔子，一对大兔子和大兔子出生的小兔子。

老师：很棒！谁将继续解释他对第二句话的理解？

出生于8：“此后，每月可以诞生一只兔子，一年之内没有死亡。”我理解这一点：毕竟，小兔子成长为大兔子，它们可以每月生下一对兔子，以及它们是小兔子还是大兔子可以健康成长而不会死亡。

学生9：我认为原来的小兔子将能够在另一个月内生下一只小兔子。

老师：我非常了解！不仅原来的大兔子可以生下小兔子，而且出生的小兔子也会长大！

学生10：对！当第一对兔子长大时，出生的小兔子会在它们长大后生下兔子，而天生的小兔子长大后可以生下兔子，他们的后代不断生下...

老师：是的！新出生的兔子可以在第三个月生下兔子，第三个月它们生下兔子的兔子。哦，我开始感到困惑...学生，你能告诉我12个月到了多少对兔子吗？

（孩子们猜测了：24对？56对？88对？超过200对...）

[评论]审查信息是解决问题的非常关键的链接。教师指导儿童按句子分析，这是非常可取的。当孩子们可以用自己的话语清楚地解释问题的含义时，问题审查工作就位了。

3。浸润想法并提出解决方案

老师：这个问题似乎真的很困难。当面对以前从未遇到过的困难问题时，我们该怎么办？

（学生不知道如何回答一段时间）

老师：老老子是我国家古代的伟大哲学家和思想家，曾经说过：“世界上困难的事情必须在轻松中完成；世界上的伟大事物必须在细节上完成。” （存在的过程软件）这句话是什么意思？

学生11：世界上所有困难的事情都可以看作是简单的事情，世界上所有主要事物都可以看作是小事。

老师（笑）：从您的解释中，我意识到，面对艰难而大事，您非常冷静。您有不同的理解吗？

学生12：要解决困难的问题，我们必须从简单的事情开始，要做大事，我们必须从小事开始。

老师：我非常佩服您的理解能力。是的，当遇到困难的问题时，我们应该从简单的事物开始，探索和发现其规则，然后使用此规则来解决此问题！现在，让我们使用这种魔术武器来解决这个问题！ （课程再次提出了兔子问题）每个人都认为，根据老挝的想法，最好从哪个月开始研究？

学生13：第一个月！

老师：为什么从第一个月开始？

生命13：因为第一个月只有一对兔子，所以这是最简单的！

老师（点头）：是的！世界上困难的事情必须以简单的方式完成！

[评论]面对一个困难的问题，老师可以轻松地穿透并将数学思想转化为学生，从而使学生能够在将这种数学思想应用于独立研究问题的过程中积累活动经验，并将“双重基础”扩展到“四个基础”中。

4。开始动手研究并解决问题

老师：现在，请要求学生独立研究这个问题！

（学生研究，教师检查和指导）

老师：学生如何进行研究？谁想在舞台上告诉我您如何学习？

学生14上台展示了一大段落的文字并解释了这一文字。

Sheng（QI）：头晕！

老师：哈哈，您可以看到您是一个非常认真的人。起初我们理解了这一点，但是后来当越来越多的兔子时，我们变得困惑。如果有人有办法更清楚地表达它，那就太好了！

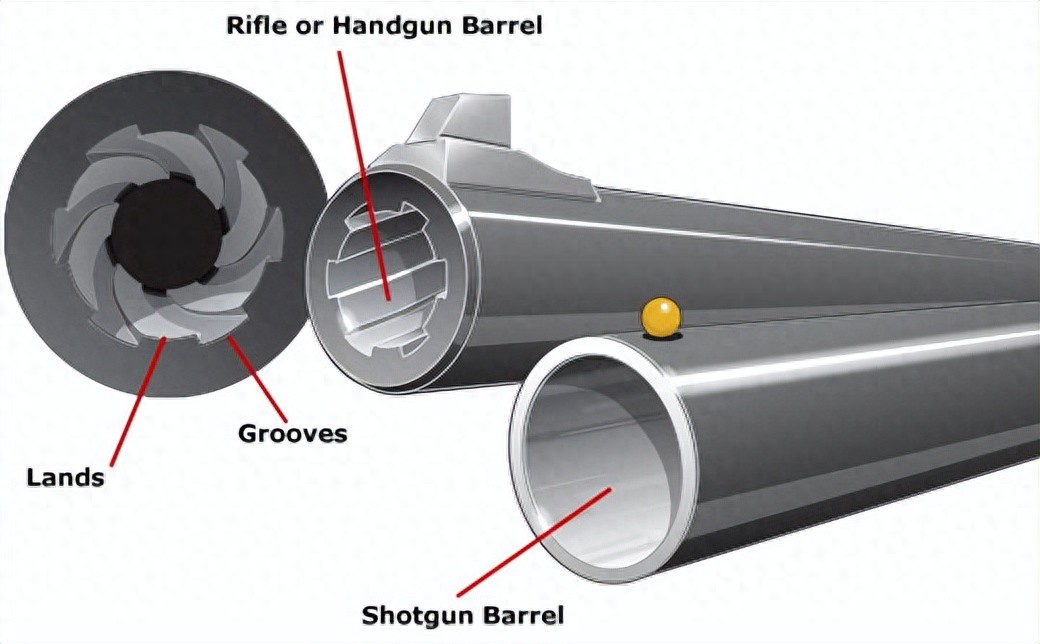
学生15显示了示意图（如图1所示）并解释了。

老师：您如何看待他的方法？

学生16：这个数字的数字是什么意思？ “ 12”是一对12只兔子吗？

学生15：不，这是第12个月。

学生17：我认为这是错误的。兔子怎么可能是11对？这些小兔子长大后仍然可以生下小兔子！您会忘记，长大后可以生下兔子！

Sheng 15尴尬地挠头。

老师：（学生15）从图片中，我们清楚地看到，从第三个月开始，每月出生一对兔子。绘画图片是数学研究的好方法，但是当绘制图片时，您应该根据问题的含义仔细考虑思考。 （学生15点点头）

老师：有不同的研究方法吗？

学生18显示了一个示意图（如图2所示）并解释了。

老师：您如何看待她的方法？

学生19：她用语言表达了这一点，这很明显，但不幸的是她还没有完成。

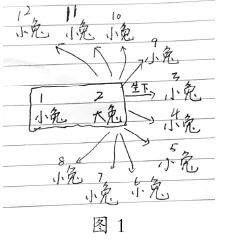
学生20：我用三角形代表一只小兔子和圆圈代表一只大兔子。我已经绘画了第五个月，有3对大兔子和2对小兔子。我还没有完成绘图（如图3所示）。

[评论]该链接使学生处于学习的最前沿，独立探索的过程是学生敏捷思维和改善智慧的过程。

老师：为了让每个人都更清晰，直觉地看到兔子数量的变化，老师准备了一些大兔子和小兔子的贴纸（在黑板上贴上一张“成对的大兔子”和“成对的大兔子”的照片），让我们一起研究。第一个月怎么了？

生活（质量）：一对小兔子。 （老师在黑板上写两行。第一行显示了第一个月的“ 1”，第二行张贴了一对兔子的图片）

老师：第二个月呢？

Sheng（QI）：这双小兔子成长为一对大兔子。 （老师在相应的位置上写了第二个月的“ 2”，并发布了1对大兔子）

老师：第三个月呢？

有21：2对兔子，即1对大兔子和1对小兔子。

老师：为什么有1对大兔子和1对小兔子？

生命21：这对大兔子是原始的兔子，这对小兔子是从大兔子出生的小兔子。 （如图4所示，老师点点头，在黑板上写信并张贴了兔子）

老师：第四个月呢？谁会来？ （Shen 22在黑板上发布了2对大兔子和1对小兔子）

老师：你为什么要以这种方式发布？

22 ：（指的是第一对大兔子）这对大兔子是一对兔子，（指第二对大兔子）上个月长大了这对大兔子（指的是这对小兔子），这对小兔子是这对小兔子，是兔子出生的大兔子。

老师：让我清楚，总共有3对兔子。那么第五个月有几对兔子呢？谁来发布它？ （Sheng 23发布了3对大兔子和2对小兔子，如图5所示）

老师：您能解释他们的生活经历吗？

生于23岁：第一对大兔子是上个月的第一对大兔子，第二对大兔子是上个月的第二对大兔子，第三对大兔子是上个月的小兔子，两对大兔子在过去的一个月和两对大兔子中占有。

老师：好的，现在他们都有身份！ （绵羊笑）第六个月有几对兔子？谁会来？

24：5对大兔子，3对小兔子，总共8对。 （张贴了兔子图片，并一一解释）

[评论]斐波那契序列的规则非常隐蔽，非常有必要为孩子提供“脚手架”。在特定的兔子图片的帮助下，孩子们清楚地解释了每对兔子的过去和现在，为下一个发现规则奠定了基础。

老师：第七个月呢？

学生25：我会做的！嘿！兔子在哪里？ （我发现兔子的照片还不够，我有点不知所措）

老师（遗憾）：似乎我们的研究无法继续，没有兔子要发布。

学生26：老师，如果您没有兔子，没关系。我们可以找到规则。我认为前面的兔子数量是常规的！

老师：是真的吗？什么是规则？

学生26：看，头几个月中的兔子数量是1、1、2、3、5和8。如果您不看前两个1，从第三个数字开始，2+1 = 3，下一个3+2 = 5，5+3 = 8，下一个应该是8+4 = 12，而第七个月则是12点。

老师（微笑）：这位同学开始找到规则，这是一个好主意！你同意他吗？

学生27：我认为，由于这是一条规则，因此从第一个数字到最后一个数字应该是一致的，只有中间数不计数。本专栏的定律是本专栏的定律。

老师（批准）：我完全同意！

学生28：我只是使用绘制圆圈和三角形的方法来知道第七个月应该是13对兔子。他计算出它等于12对兔子，这绝对是错误的！

老师：是的，实践带来了真实的知识，您会知道他的猜测是否在实际画上。既然每个人都认为他发现的规则错了，那么这组数字的规则是什么？

（教室很安静，孩子们正在观察和仔细思考）

学生29：老师，我发现每个月的大兔子数量是上个月的兔子总数，而小兔子的数量是上个月的大兔子数量。

老师：哦？是真的吗？

Sheng（QI）：是的！是的！

老师：您还发现了什么？

学生30（兴奋）：老师，我还发现每个月的兔子数与前两个月的兔子总数完全相同！也就是说，本月的兔子数量等于上个月的兔子数量加上上个月的兔子数量。

老师（困惑）：这是真的吗？让我们一起检查一下。

（孩子们热情地检查）

学生31：他是对的！例如，第五个月是5对兔子，这完全等于第四个月的3对加上第三个月的2对。

生命32：第六个月是8对兔子，相当于第五个月的5对，再加上第四个月的3对。

学生33：我已经测试了所有这些。每个月的对数等于前两个月的对数之和！您会看到，第三个月的兔子对数是1+1 = 2，2； 1+2 = 3，3是第四个月的兔对数，其次是2+3 = 5，3+5 = 8，5+8 = 13 ...

老师：停止！停止！不只是照顾一切，您会给所有人一个机会吗？让我们遵守此规则，并计算出第八个月份将有多少对兔子以及它们的产生方式。

学生（x）：21对，8+13 = 21。

老师：第九个月呢？

Sheng（QI）：34对。

老师：第10个，第11和12个月呢？

Sheng（QI）：分别为55对，89对和144对。

学生34：233对！ 377对！

（整个班级大笑）

老师：您看到，一个人一开始就发现这非常困难。通过从最简单的事物开始，发现规则，可以很容易地解决它，甚至说出在第13个月和14个月中有多少对兔子。难怪我说：“世界很困难，必须以一种简单的方式完成。”但是我想提醒所有人，我们不应该忘记班上的第一个同学发现这种模式。他是谁？

生活（QI）：生命30！

老师：他是一个擅长观察和思考的孩子。我们将给他最热烈的掌声！ （老师和学生称赞）

[评论]多轮模拟的真实物体贴纸使孩子们了解每对兔子的来龙去脉。老师在正确的时间删除了“脚手架”，促使学生的思想从简单的直觉操作转变为寻找抽象序列规则。通过观察，错误识别，验证和推理，孩子们发现了序列规则，并对句子做出了回应：“所有美丽的事物都以曲折的方式实现了他们的目标！”

5。序列简介，揭示主题

老师：我们刚才研究的问题是数学史上著名的兔子问题。意大利数学家斐波那契在研究兔子问题时发现了这个有趣的序列，因此这个序列以他的名字命名，称为斐波那契序列。 （黑板主题：fibonacci序列）您能告诉我哪种序列用您自己的话称为斐波那契序列？

学生35：添加前两个数字等于第三个数字。

学生36：序列中的数字符合等于前一个数字的两个数字的定律。

老师：让我们看一下数学家总结的规则。 （课程介绍了斐波那契图像和斐波那契序列文本的引入，大声配音：一个序列。如果每个项目是第三项中的前两个术语的总和，那么我们将这样的序列称为斐波那契序列），而数学家发现的序列是与我们今天研究的成绩完全相同的序列！看来成为一名伟大的数学家并不是一件深远的事情。如果我们出生于几百年前，那么这个序列可能不会被称为斐波那契序列，而是以我们的同学名字命名！

（孩子们很高兴地笑了）

6。与生活联系并扩大扩展

老师：除了兔子的繁殖外，自然界中还有许多生物按照斐波那契序列的定律生长。 （课程显示了一棵树的图片）这个普通分支在普通人眼中可能没有任何美丽，但是只要您仔细观察，您就会发现其成长过程具有某些规则。从数学的角度来看，我们将其增长周期分为几个阶段，然后观察其分支。你发现了什么？

创世记37：第一阶段是一个分支。

创世记38：第二阶段，它仍然是1个分支。

在第三阶段，已经成为两个分支，一个新的小分支从原始分支中倾斜地生长。

第40代：在第四阶段，总共有3个分支。一个大分支是原始分支。一个大分支在第三阶段从小分支生长。一个小分支从大的分支中生长。

...

（老师和学生将每个阶段中的分支机构数计为一起，并同时将它们呈现在课程中，如图6所示）

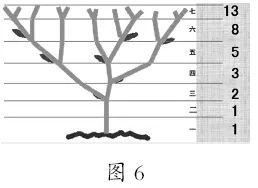
老师：您发现了什么？

学生41（令人惊讶的是）：这继续向上增长，这是斐波那契的序列！

Sheng（QI）：是的！是的！

老师：当然，这种完美的斐波那契序列在自然界中很少见，因为生物的生长始终受环境的影响。有一个说法：“生活有时是诞生的，是有序的。”这意味着一切的增长都有自己的规则。只要您仔细观察，您就会发现它们的大多数成长模式可以用数学语言描述。请观看视频：

在中世纪，意大利数学家斐波那契向人们揭示了一个有趣的顺序。如果仔细观察，您会发现从第三个项目开始，每个项目都是前两个项目的总和。

走进斐波那契序列开元ky888棋牌官方版，您会感到它的魅力。我们在斐波那契序列中的每个数字作为侧面长度绘制一组正方形，并在每个正方形中绘制四分之一的圆周，以便出现美丽的螺旋形。优雅的螺旋在不断伸展，并向我们展示了美丽的Nautilus。 （演示在斐波那契序列中的每个数字作为正方形的侧面长度，螺旋线绘制螺旋线，螺旋线延伸到美丽的nautilus中）

如果您深入研究，您会发现斐波那契系列的两个相邻术语的比率正在接近黄金比率。向日葵的种子以黄金角度分散，花头是最浓，最强的。目前，两组向前和反向螺旋将同时出现。 Although the number of forward and reverse spirals will vary depending on the type and size of the sunflower, they are always two consecutive Fibonacci numbers. (Show the seeds of sunflowers are arranged divergently according to the ratio of two adjacent numbers in the Fibonacci sequence, becoming dense sunflowers) (Students can't help but exclaim)

Teacher: Just now, we found the Fibonacci sequence from the growth of branches, the Fibonacci sequence in the shell of the Nautilus, and the Fibonacci sequence in the arrangement of the seeds of the sunflower. Then I have a question: have they discussed the branches, nautilus, and sunflower seeds in advance?

Sheng (Qi Xiao): No!

Teacher: Then they discussed with the rabbits?

Sheng (Qi Xiao): No!

Teacher: Then did they discuss with Mr. Fibonacci?

Sheng (Qi Xiao): No!

Teacher: Since there is no discussion, what kind of power is it that makes the growth of these creatures surprisingly consistent?

Sheng (Qi): Nature!

Teacher: Yes! Therefore, the Fibonacci sequence is also called "the password of nature" and "God's fingerprint"! Nature is so precise and so incredible. Is this a coincidence or an inevitable? All of these need to be thought about and explored in the future. This is the end of this class, and the get out of class ends!

[Commentary] The teacher led the children to observe the branches and discovered the Fibonacci sequence hidden during their growth, and then used videos to dynamically show the magic of the Fibonacci sequence in nature. During the perfect presentation of the courseware, the children involuntarily exclaimed and fully appreciated the beauty of mathematics. At the end of the class, the teacher also seized the opportunity to make a humorous song. The humorous and interesting language inspired the children to explore the world and explore the unknown in an endless motivation.