数学园地|015数学跨学科:有趣的斐波那契数列

数学花园015
数学跨学科:有趣的斐波那契序列
您是否仍然记得上周六举行的第14个国立大学学生数学比赛数学的第三个问题(11.12)?

您知道这个问题主张的背景吗?快来找到本文的答案!

今天,数学花园将向您介绍一个有趣的序列-Fibonacci序列。
斐波那契序列的起源
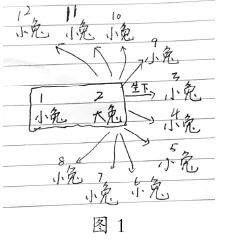
斐波那契序列的出现可以追溯到13世纪。意大利数学家斐波那契在他的“算盘书”中提出了一个有趣的问题:一对兔子每月生下一对兔子。小兔子在出生的第二个月中是成年人,每个月开始生下一对兔子。假设出生的所有兔子都是一名雌性和一名雄性,并且生存,一年中有几对兔子?通过计算,每月的兔子对数总数为:1、1、2、5、8、13、21、34、55、89、144。如果没有限制,将有233、377、610 ...通过“兔子序列”的汇编,我们将发现fibonacci序列的第三个术语与第三个术语相等,并且是等于第三个术语的总和。该规则被定义为使用数学公式的递归方法:
该序列称为斐波那契序列[1]。
【“兔子”序列】
斐波那契序列与自然之间有许多“巧合”
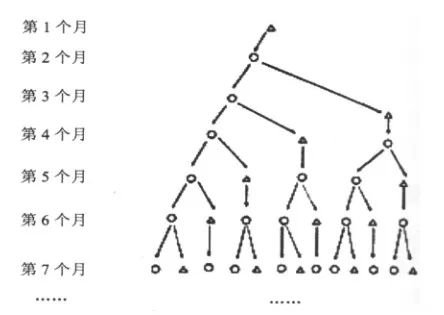
斐波那契序列与自然具有许多“巧合”,并且在自然科学的其他分支中都有许多应用。例如,一棵树的生长通常需要一段时间的“休息”时间才能自身生长,然后新的分支机会发芽。因此,在一个间隔(例如一年)之后,树苗就会生长一个新的分支。新的分支在第二年“休息”,旧分支仍然发芽。此后,旧的分支机构和分支机构同时萌芽了一年,以及那一年在明年“休息”的新分支机构。这样,树的每一年的分支数量形成斐波那契序列。该法律是生物学上著名的“鲁德维格定律” [2]。
rudwig的法律】
许多植物种子的排列也与这种神奇的序列有关。例如,向日葵种子的排列由逆时针螺旋和顺时针螺旋组成。如果您仔细观察螺旋的数量,您会惊讶地发现它们始终是两个相邻的斐波那契数。这种螺旋也存在于松锥和菠萝中。植物种子以这种模式排列,使种子堆叠效率最高[3]。

【斐波那契数植物板的数量】
此外,几乎所有花的花瓣数都遵循斐波那契序列的常规图案。例如,兰花,茉莉花和百合具有3个花瓣,Ranunculus植物有5个花瓣,去凝胶有8个花瓣,万寿菊有13个花瓣,紫色的花瓣有21个花瓣,雏菊有34、55或89花瓣[2]。它们神奇地符合斐波那契序列的递归布置。
黄金螺旋,黄金分割和连续分数的完美统一
我们使用斐波那契数作为侧面长度来制作正方形并将其碎成矩形,然后矩形将无限接近具有约0.618的纵横比的金矩形。如果在每个正方形的侧面长度作为半径中绘制风扇,则连接到这些风扇形状的弧形是斐波那契螺旋的,也称为“金螺旋式” [4]。
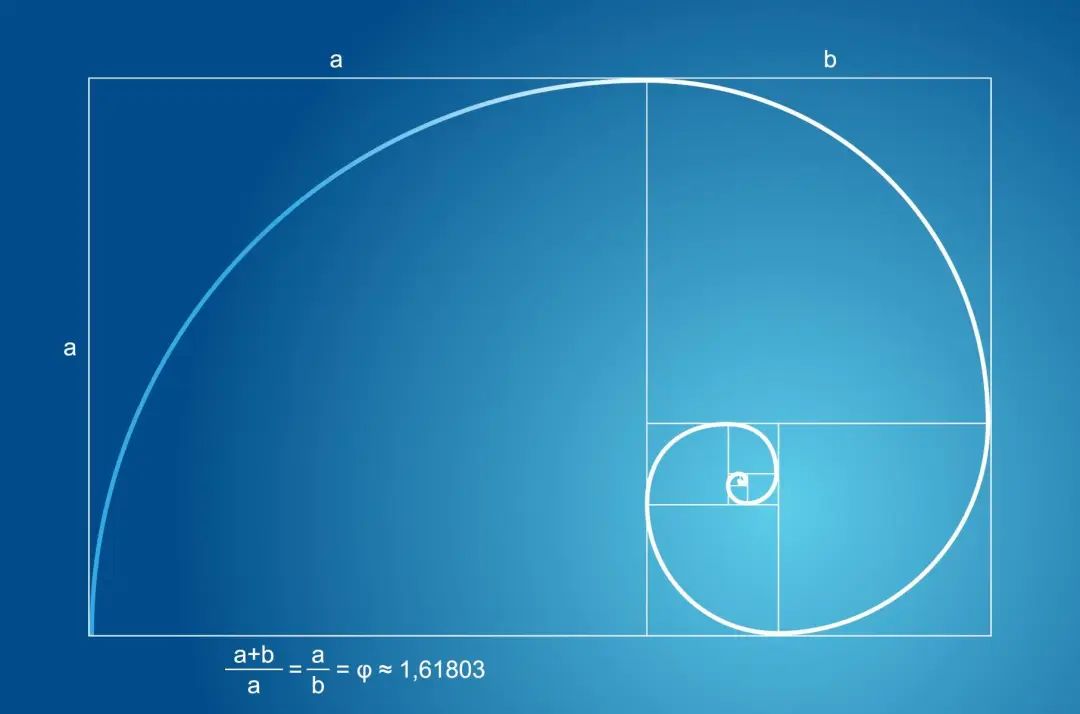
有趣的是,自然界中有许多类似于螺旋线的模式,例如飓风,银河系,向日葵,蜗牛壳等。它们的螺旋线与古希腊的毕达哥拉斯提出的黄金比例一致,并且是斐波那契的螺旋线。
通过观察斐波那契序列及其衍生的螺旋线,我们可以发现,随着术语数量的增加,每个项目与前一个项目的比率:,,,,...越来越接近我们所说的黄金比率:0.61803398 ... [6] “黄金比率”是目前熟悉的数学关系,这是一种古老的数学方法。起初,毕达哥拉斯学校在五角星发现了黄金比例,并用它来解释建筑物,雕塑等的艺术形式。根据黄金比率的数学关系建立的建筑物[7]。斐波那契螺旋中的黄金比率使这种极其理性和美学的曲线充满了视觉效果的严格结构和完美的顺序,从而为我们带来了舒适的视觉体验。两者之间的内在关系使斐波那契序列更加神秘和迷人。
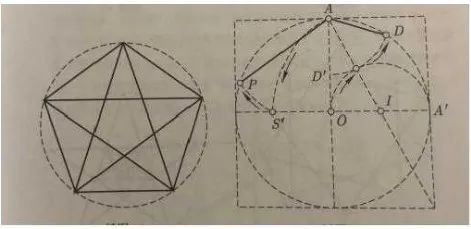
【五个尖星中的金色分区】

[世界著名的绘画和黄金螺旋]
我们知道黄金比是满足方程式=的黄金比率开yun体育官网入口登录app,因此有= 1-x,即x(x+1)= 1。您可以得到x =,而不是在等式右侧的分母中的x。等等,您可以连续分数并得出结论:
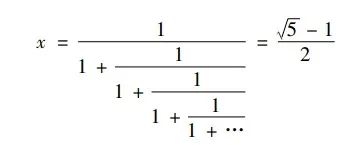
依次削减连续分数以获取:
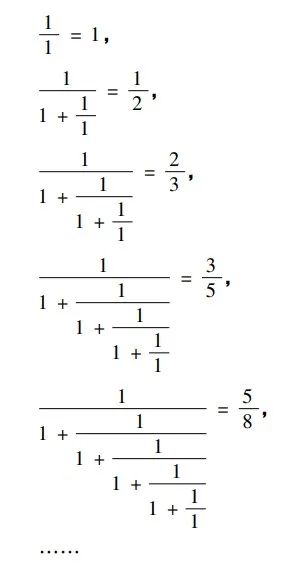
我们按顺序排列了该连续分数的近似值,以获得这些近似值的分子和分母是斐波那契序列中的项,因此在斐波那契序列中有两个相邻项的比例。当N∞时,其极限恰好是黄金比率。
黄金分割,斐波那契数和无限连接的分数在内部数学关系中显示出完美的统一[6]。
斐波那契序列的一般公式

在这里,我们展示了使用特征方程(主要代数解)求解二阶线性递归序列(除线性代数方法,父函数方法等)的特征方程。
令人惊讶的是,斐波那契序列中的每个项目都是一个积极的整数,其一般公式实际上包含不合理的数字!
斐波那契序列的特征
从第二项开始(构成一个新序列,第一个项为1,第二项为2,... ...)每个偶数的平方比上一项的乘积和下一个学期高1个,每个奇数术语的平方比上一项的乘积小于1个。例如,第二项1的平方比上一项1和下一个学期2的乘积小1,第三项2的平方大于其上学期1和其下一个学期3的乘积。可以通过获得该计算来获得计算。
这是数学A中第三个问题的命题背景,这是今年第14届全国大学学生数学竞赛(计算矩阵A的K功率的前几个术语,您发现了什么?)。如果您知道此属性,则可以通过基本代数的方法直接解决此问题。此外开元ky888棋牌官网版,斐波那契序列的特征很多,例如奇数项的求和公式,偶数的求和公式,正方方项的求和公式,间隔项的关系,双项的关系,双项的关系等,在这里尚未详细介绍。

简短摘要
除了本文中提到的内容外,还有许多关于斐波那契序列的有趣数学研究,例如斐波那契序列中的操作特性,与扬hui三角形的连接,mantissa循环,向卢卡斯序列的扩展等等。在我们的生活中,有更多的斐波那契序列或斐波那契螺旋,例如在建筑设计和美学领域的应用研究;在现代物理学,准晶体结构,化学等中,斐波那契序列也已成为越来越直接的应用……有趣的斐波那契序列是由自然选择的,我们发现的开元ky888棋牌官方版,并最终由我们应用。
参考
[1]张最低。数学文化和案例。天津科学技术出版社,2020.09。
[2]小米。有趣的斐波那契序列[J]。江苏教育学院杂志(自然科学版),2011,27(05):31-33。
[3]差异。植物如何优化器官排列? - - 斐波那契螺旋[J]。科学24小时,2004(05):24。
[4] Chen Zhengyu。突破性和从斐波那契序列到分形的几何艺术美学[D]。西安美术学院,2020年。Doi:10.27399/d.cnki.gxamx.2020.000018。
[5]张小。美丽的金部法律[J]。农村青年科学研究,2017年(Z2):85。
[6]张Xiong。黄金分割及其应用的美学意义[J]。自然辩证法研究,1999年(11):5-8.DOI:10.19484/j.cnki.1000-8934.1999.11.002。
[7]他丹,刘yin。让数学文化进入教室 - 以“黄金分区”为例,以“黄金分区”为例[J]。阅读,写作和计算,2022(06):198-200。
欢迎每个人批评和纠正我,并将数学交流在一起!

手稿| Cao Jiahui
编辑| Cao Jiahui
评论| Pan Qian和Zhao Liyu