伯努利试验及大数定律

作者| [美国]威廉·邓纳姆

翻译|冯苏

来源|摘录摘自“数学事物：巨大的问题和非凡的人”，《人们的帖子和电信出版社》，2022年3月。[有趣的数学]有权转载，谢谢您！

首先，伯努利实验不是佛罗伦萨的法律程序，而是主要概率理论的基础，并且在我们对不确定世界的理解中起着重要作用。

Bernoulli测试是一个简单的测试，有两个结果。它的结果是成功或失败，黑色或白色，打开或关闭。没有中间位置，没有妥协的空间，没有优柔寡断的舒适感。

这样的例子太多了。我们观察到一张从黑色或红色牌中取出的卡片。我们分娩一个女孩，无论是一个女孩还是男孩。我们经历了24小时的一天，要么遇到流星。在每种情况下，将一个结果设计为“成功”，而另一个结果将“失败”设计为方便。例如，选择一张黑卡，有一个女儿或不遇到流星可以被标记为成功。但是，从概率的角度来看，选择一张红牌，儿子或遇到流星不会有任何区别。在这种情况下，“成功”一词没有以价值为导向的颜色。

单一的Bernoulli实验没有多大意义。但是，当我们反复执行伯努利试验并观察其中有多少个试验成功以及其中有多少人失败时，事情变得有意义。这些累积记录包含许多潜在的非常有用的信息。

当我们进行实验时，会有一个关键条件：这些重复的试验必须彼此独立。独立一词不仅是专业定义的，而且还传达了适合我们目标的含义：如果一个事件的结果永远不会影响另一个事件的结果，那么两个事件将彼此独立。例如，史密斯有一个儿子，约翰逊有一个女儿是两个单独的事件。例如，扔一角硬币并扔掉一角钱（前或反向）的结果也彼此独立，而一枚硬币的结果不会影响另一硬币的结果。

但是，如果我们在一张卡片牌中学习两张牌，一次只能绘制一张卡片，并认为黑卡成功，那么当我们绘制第一张纸牌，然后是第二张卡片时，独立性就会丢失。这是因为，如果第一张卡是李子a（一个成功），它将影响第二次抽奖结果 - 它会降低第二次绘制黑卡的可能性，并且第二次绘制A的可能性也减少了，绝对不可能画梅花A。

幸运的是，这种缺乏独立性可以通过简单的对策进行补偿。绘制第一张卡后，将其放回原始卡中，再次将其清洗，然后再次绘制。由于我们的第一张卡已重新混合到原始卡中，因此其身份对第二张平局没有影响。从这个意义上讲，独立事件需要为每个试验创建一个不可追踪的平台，以使每个试验成功的可能性保持不变。

伯努利实验的最独特的例子出现在游戏游戏中，例如投掷硬币或骰子。对于硬币而言，每个投掷显然都是独立的，因此成功的可能性（例如获得阳性的概率）是相同的。说硬币是“平衡”的，这意味着概率正好是1/2。对于统一的骰子，如果我们指定3个成功，那么我们的成功可能性总是1/6。

但是，如果我们扔硬币五次会发生什么？在这五次掷球中获得三个前线和两个逆转的概率是什么？通过扩展，如果我们将这枚硬币扔到500次，那么获得247个正面和253个后座的可能性是多少？这似乎是一个噩梦问题，但其解决方案出现在Jakob Bernoulli（1654-1705）中，这是概率理论的早期杰作之一。

伯努利（Bernoulli）是瑞士的本地人，他的祖父，岳父和岳父都是富有的药剂师。他放弃了在大学学习神学的迫击炮和治疗学，并在22岁时获得了学位。但是，尽管他的家人都与医学有关，他接受了传教教育，但他真正感兴趣的是数学。

从1770年代后期到他去世，伯努利一直是世界上最杰出的数学家之一。他是个天才，但个性很烦人。他自大，对那些没有才华的人的努力嘲笑。例如，在研究了今天所谓的“伯努利号码”（以纪念他为单位）之后，伯努利发现了一个非常聪明的捷径来概括积极整数的力量。他说：“我在不到七分钟半的时间内使用了它”，并确定了前1000个正整数的十足者的总和。换句话说，他在不到十分钟的时间内确认了以下结果：

这确实是一个巨大的。但是在一个自写的评论中，他吹嘘自己的捷径“清楚地表明了Brio的工作是多么无用……他（Brio）只是付出了很多努力来计算出强大之上的前六个，我在一页中完成了计算纸”。这个人对可怜的伊斯玛尔·贝拉德斯（Ismael Bullialdus）没有同情，他不仅拥有数学家的非凡见解，而且具有异常自负的自我。

雅各布·伯诺利（Jacob Bernoulli）的峰值时期是戈特弗里德·威廉·莱布尼兹（Gottfried William Leibniz）发现了微积分的时候，雅各布是普及这一富有成就成就的重要人物之一。像任何新开发的理论一样，微积分受益于那些跟随开拓者的脚步的人，以及他们的才华比莱布尼兹（Leibniz）的才华较低的学者，莱布尼兹（Leibniz）的贡献是解决这个主题，这是必不可少的。雅各布就是这样的贡献者。

[由瑞士巴塞尔的BirkhäuserVerlag AG转载，这是“ Jacob Bernoulli的完整作品，第1卷：Nova，自然哲学”，由Jo Fleckenstein于1969年编辑。

出于这个原因，他有一个令人不安的盟友，约翰（1667-1748），他的弟弟，与他的名字相同的首字母，这是伯诺利（Bernoulli）的极其才华但喜欢吵架的兄弟。 。实际上，雅各布曾经是他哥哥的数学老师。在接下来的几年中，他可能会很遗憾地教约翰如此之后，因为弟弟被证明是一位与他相提并论的数学家，甚至超越了他。两兄弟为数学霸权竞争。当约翰解决了一个曾经使他的兄弟迷惑的问题时，他总是没有掩饰自己的兴奋，尽管雅各布故意打电话给约翰为他的“小学生”，这意味着约翰只是跟随他的导师。伯诺利都不被认为是高贵的人。

著名的冲突源于链条线的问题。链状是由固定在壁上两个点的链链夹形成的曲线（见图B-1）。那些熟悉代数的人可能会猜测链条沿着抛物线弧悬挂，这是一个完美的逻辑猜测，早在17世纪初就被伽利略这样的人物想到了。但是像这样悬挂的连锁店不是抛物线。到1690年，雅各布·伯诺利（Jacob Bernoulli）正在研究很难确定这条曲线的真实身份，也就是说，他想给出其方程式。

图B-1

事实证明，雅各布没有胜任任务。当约翰给出答案时，不难想象雅各的惊喜。后来，当炫耀自己的胜利时，约翰说，为此解决了这个解决方案，“我全天全夜研究了这一点，没有休息。”他的烦人技巧和他的才华一样出色，约翰赶到雅各，并向他努力思考的哥哥讲了答案。雅各布突然感到沮丧。

但是，雅各布想进行他的“报仇”。这次战场是所谓的简单周问题，它是指区别哪个曲线将最大的区域与相同的周边围起来。我们将在第一章中更详细地讨论这个问题，但是现在我们可以首先研究雅各布·伯诺利（Jacob Bernoulli）如何使用微积分来描述1697年的这个问题。他将处理一个称为三阶微分方程的困难数学对象，这是一项工作这为现在称为“变性”的新数学分支的道路指向了广泛的研究前景。

弟弟约翰（John）与他有不同的看法，并说这个ISO周的问题已经通过相对简单的二阶差分方程解决了。就像过去的伯努利一家一样，他们的争吵变成了对抗，最终只是因为缺乏“弹药”而停止了。

约翰·伯诺利（Carnegie Mellon University图书馆Huiyun）

但是，这次是雅各上一次笑了，因为他的弟弟的二阶微分方程是不正确的。不幸的是，雅各布实际上没有机会嘲笑他，即使嘲笑他，因为他于1705年去世，而约翰对这个问题的错误解决方案仍然神秘地在巴黎学院的办公室被神秘地密封。有一个猜测，约翰已经意识到了自己的错误，并设法秘密地隐藏了它，这样他就不必忍受公众的屈辱并让他的兄弟嘲笑它。

这些有趣的事情完全证明了他们的兄弟之间的分歧，因此下面发生的事情并不奇怪。当时，约翰被认为是编辑他新死亡的兄弟论文的最合适的人，但是雅各的寡妇停止了它，因为她担心复仇的约翰会摧毁雅各布留下的数学遗产。 。杰·霍夫曼（Je Hofmann）可能最能描述雅各布在科学家传记词典中的个性：“他是故意，顽固，进取，报复和受到自卑的困扰，但他对自己的才能充满信心。由于这种个性，他将不可避免地拥有这种性格。与他的个性相同的弟弟冲突。 。

让我们不要谈论他们的兄弟之间的竞争，让我们回到上面提到的概率问题：如果抛出统一的硬币五次，三个阵线和两个反向的概率是多少？在“猜测”中，雅各布·伯努利（Jacob Bernoulli然后由以下公式给出了N成功和M失败的概率。

为了简化上述公式，数学家介绍了阶乘符号：

例如，3！= 3×2×1 = 6，5！= 5×4×3×2×1 = 120。 （请注意，阶乘中的感叹号不需要我们大声说话。）凭借这种方便的符号，伯诺利的结果将减少为：

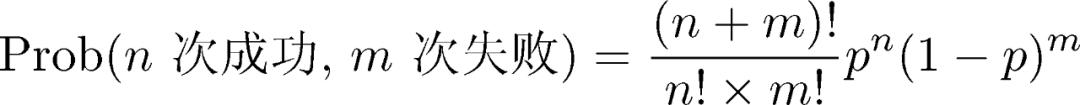
因此，在扔了统一的硬币五次之后，获得三个前线的概率是设置n = 3，m = 2和p = prob（射击a前）= 1/2。所以有

同样，为了投掷骰子15次并获得五个4s，我们声明获得4是“成功”，指定的值是：

因此，在15个独立投掷后，获得5 4的可能性为

这几乎是不可能发生的事情。

回到一个较早的问题，扔硬币500次，获得247个额叶和253个反转时间的可能性是

尽管此结果是正确的，但概率太复杂了，无法手工计算，甚至高端袋计算器也无法达到计算500的愿望！如此大的数字（那些怀疑的人可能希望尝试一下）。我们将看到一种在第N章中近似于解决此概率的技术。但是，即使无法直接计算这样的计算，该公式在理论上是完美的。它是找到任何一系列独立Bernoulli测试的可能性的关键技术。

不幸的是，日常生活中的大多数事件实际上比扔硬币要复杂得多，这几乎纯粹是概率的情况。确定25岁的年龄超过70年的可能性开元ky888棋牌官网版，或确定下周二降雨超过1英寸（25.4毫米）的可能性，或确定正在进入交叉路口的汽车的概率右转，解决这些问题绝非易事。这些事件是无助的，因为现实世界的复杂性，正如雅各布所说：

我想问，我可以列出所有可能的情况以确定在人体不同地区和不同年龄遭受折磨他的致命疾病的数量吗？换句话说，如果可以确定一种疾病比另一种疾病更致命，例如瘟疫会导致死亡比水肿更多，或者水肿可能导致死亡而不是发烧，那么基于这种理解，就可以预测未来的一代。生存与死亡之间的关系吗？ [6]

这种概率超出了数学范围吗？概率理论可以归类为模拟游戏吗？

伯努利在那本书中对这个问题给出了非常有力的答案，也许是他最大的遗产“猜测”。实际上，他称这个问题为“黄金定理”，并写道：“就其新颖性和强大的实用性而言，加上更大的难度，该定理是由于其体重和价值造成的，它已成为该理论中最重要的部分“今天所谓的伯努利定理是大量的定律，它被认为是概率理论的主要主体。

要了解其性质，再次假设我们正在进行一项独立的Bernoulli试验，在该试验中，每个试验成功的可能性是P。我们知道操作的测试总数，称为N，以及成功结果的测试数量，称为x。因此，x/n的分数是我们观察到的成功的比例。

例如，如果抛出统一的硬币100次，并且产生了47个正面，则观察到的额比为47/100 = 0.47。如果硬币被抛出100次，并且产生了55个前线，则总成功比为

只要硬币折腾不懈，就没有理由阻止其他人将硬币扔100次或投掷1亿次。关键问题是，经过长时间的操作，成功比率X/N会发生什么变化？

随着试验数量的增加，没有人惊讶地发现该比率接近0.5。一般而言，当n变大时，我们将看到x/n的值趋向于固定数字p，这是任何单个试验成功的真正概率。因此，此处显示了该定理的功能。当成功p的概率未知时，在大量实验中，成功的比率P应该是更好的估计值。由符号指示，我们应该写它，

，当n更大时（含义“大约相等”）

添加一些重要条件，这成为大量定律。伯努利（Bernoulli）的定理之所以如此出名的原因不是因为它揭示了一个真理，而是因为很难用严格的论点证明这一点。雅各本人在他的高度代表和讽刺的语言中承认：“即使是最愚蠢的人也应该能够本能地理解（大量的法则）。”但是，为了给出正确的这项法律证明，他付出了二十年的努力工作，并证明了他给了几页“猜测”的证据。事实证明，他的评论“这一原则的科学证明并不是那么简单”是故意轻描淡写的。

我们应该讨论上面提到的有关伯努利定理的“重要条件”。因为这本质上是概率陈述，所以应该随时可能发生的不确定性。我们不能绝对确定，将硬币1000次投掷的比例接近0.5，而仅扔硬币的比例仅100次会更大。投掷100次时，完全可以产生51个前线，并且在投掷1000次时只能产生486个前线。因此，此“小样本”估计X/N = 51/100 = 0.51实际上应该比“大型样本”估计X/N = 486/1000 = 0.486更接近抛出正面的概率。这样的事情很可能会发生。

这样，如果我们再掷1,000次，那么每个掷球并非完全不可能产生前线。有可能产生惊人的结果，2000次投掷导致了1486次额叶，因此估计的概率为1486/2000 = 0.743。在这种情况下，大量法则似乎不正常。

但事实并非如此。因为雅各布·伯诺利（Jacob Bernoulli）证明，对于任何给定的小公差，例如0.000 001，估计的概率x/n和真实概率p之间的差异是这种较小的公差或比学步较小的可能性，只有1个，只有1个试验数量增加。只要我们进行足够的实验，我们几乎可以确定或使用伯诺利（Bernoulli）用来在道德上使用的单词，即我们的估计值x/n与真实概率P之间的差异必须在0.000 001之内。当然，我们不能是100％确保P和X/N之间的差异小于0.000 001，但是大量实验可以完全肯定这种推断并不太离谱。

在上述情况下，扔硬币2，000次并投掷前线的可能性估计为0.743，在阅读本章时，这可能比一个人遇到流星的可能性要小。此外，即使出现了这种不可能的估计，伯诺利仍然充满信心地声称，通过进行许多实验，例如2000、200万或更多实验，该比率x/n必须趋向于0.5。

重要的是要强调的是，即使有很少的限制，大量定律仍然是可靠的。这与我们在生活中遇到的其他著名法律不同，例如墨菲定律和普遍重力定律。它们要么是公认的陈词滥调（例如墨菲定律），要么是高度赞扬的物理模型（例如重力定律），必须根据证据在任何时候纠正它们。但是，大量定律是一种数学定理，已经证明它将始终在必须遵循的逻辑限制下。

此外，它有其自己的目的。保险公司用于调整精算表的生存概率是基于大量类似实验（例如人类生存和死亡）的结果。天气预报员预测降雨的可能性也是如此。

或以这样的例子为例，回到18世纪，要求女人生下一个男孩而不是女孩的可能性。如何以某种方式计算此概率？继承的复杂因素严重破坏了让男孩事先使用纯粹理论方法的概率。因此，我们被迫使用伯努利定律作为处理它的武器来使用“伪造”或验证后。

在18世纪初期，这个特殊的问题在英国约翰·阿布斯诺特（John Arbuthnot）的心中徘徊。像其他前任一样，他从人口记录中指出，每年出生的男孩的出生比女孩多一点，并认为这种失衡已经存在“多年来，不仅在伦敦，而且在世界各地”。阿巴特诺（Abathnot）试图在“上帝的祝福”的帮助下说明这种现象。几年后，雅各布和约翰的侄子尼古拉斯·伯诺利（Nicholas Bernoulli）继承了家人拥有的数学才能，并使用大量法则得出结论，男孩的可能性是18/35。换句话说，大量的出生记录显示出巨大而稳定的趋势，男女比例为18至17。伯努利的定理“不仅在伦敦，而且在世界上也应用”。

直到今天，它仍然有效。在Bernoulli定理和计算机的力量的帮助下，一种称为Monte Carlo方法的技术已经变得非常重要，因为它可以帮助科学家以一种概率模式模拟广泛的随机现象。这是蒙特卡洛法的一个相当简单的例子。假设我们想找到不规则形状的湖面表面的表面积。我们可以沿着湖泊行走，也可以向下拍照，但是湖的弯曲及其不规则的边界使得难以通过任何数学公式来确定其面积。

假设我们的湖在图B-2中是阴影的形状，我们给了图上的总和。因为我们计划在第L章中重新审视此示例，所以我们选择了一个具有相对规律的湖泊，这是一个湖泊开yun体育官网入口登录app，其抛物线是由轴和方程式界定的。

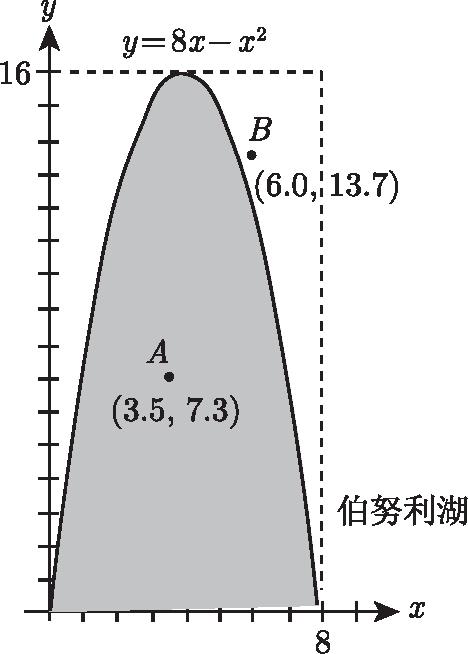
图B-2

我们将使用概率方法来估计其面积。首先，如图所示，将矩形内部的区域圈出。其次，让计算机在此矩形中找到任意数量的（x，y）点。例如，计算机可能能够找到图a =（3.5，7.3），b =（6.0，13.7）中显示的两个点。

现在，我们必须问计算机：这些随机点是否落入了这个湖泊或湖外？就我们而言，这个问题很容易解决。检查点A，我们在抛物线方程中让X = 3.5，然后找到相应的值。这表明点（3.5，15.75）在抛物线上。因此，比较点A，点A的第一个坐标是相同的，而第二个坐标仅为7.3，它落入抛物线（即湖中）。

同样，在考虑B时，我们将其在抛物线方程中的第一个坐标代替以获取相应的值。因此，点（6，12）位于抛物线上，因此B点（6，13.7）落在抛物线外，并撞到干燥的地面。只需几毫秒即可选择很多随机点，并确定它们是在湖中还是外部。

现在，让我们根据蒙特卡洛方法来看一下关键观察：将随机选择点落入湖中的确切概率记录为p开元棋官方正版下载，这是湖面占据的矩形区域的比例， IE

当然，我们只能通过了解该湖的面积来计算这种概率（这正是我们需要的未知数量）。但是，我们可以估计基于X/N落入湖泊的点的概率P，即抛物线内部的部分的比例。使用长期成功率近似真正的概率本身就是大量定律的直接应用。

在此示例中，我们的计算机在矩形中选择了500点，发现其中342个掉入了湖中。因此，我们估计

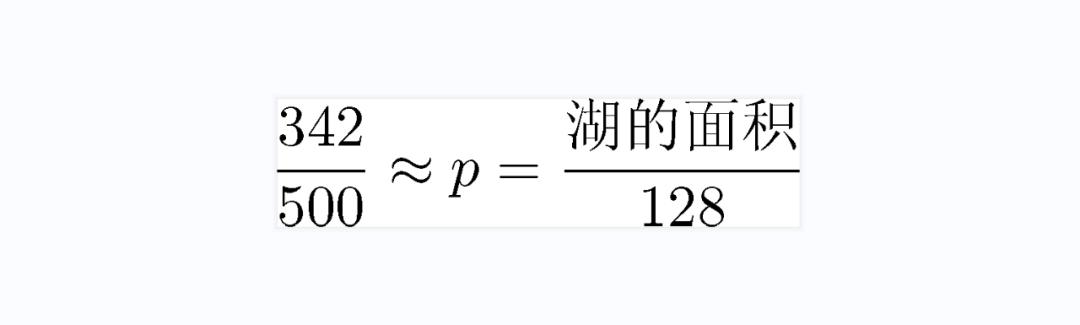
跨越跨越后，此估计是

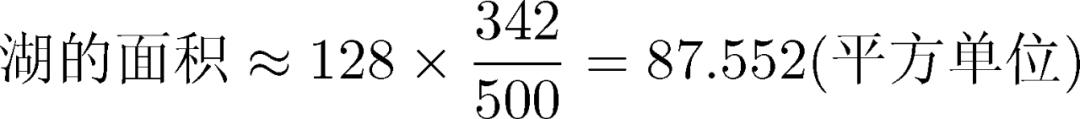
因此，没有其他任何帮助，只需使用大量的伯努利定律，我们就会对湖面区域进行粗略的近似。

我们如何获得更准确的估计？我们只简单地让计算机选择5000点而不是此矩形中的500点。在此示例中，它发现该湖中有3293点，所以

所以有

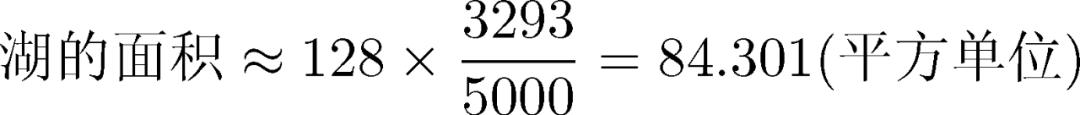
当然，我们还可以让计算机选择50,000个随机点或500,000点，或者使用功率让其选择尽可能多的点。然后，我们将更有信心对这个抛物线湖的区域进行估算。

这是一个基本的模拟示例，可以使用Monte Carlo方法研究现实世界中许多更美好的现象。此外，正如我们稍后将看到的那样，示例中抛物线的面积实际上可以通过积分方法准确地获得。但是这个例子仍然使我们感受到概率的力量。

自雅各布·伯诺利（Jacob Bernoulli）证明了他的伟大定理以来，已经过去了三个多世纪。他的原始论点被简化的版本所取代，该版本更有效地反映了这件事的本质，这种情况在数学中很常见。今天的标准证明是基于俄罗斯数学家Chebishev的结果。在一页上的大量定律中，同时表明伯努利的证据确实很麻烦。但是，凭借伯努利不具备的宽容精神，我们将坚定地抵制这样的想法，即仅是因为伯诺利的证明是章节来澄清的，“我们只需要一页即可完成这项“工作”，他将他的工作标记为“”为“”。无用”。

这是进步的常态。但是，在全人类的斗争中，我们应该记住这些前辈。正如今天的音频技术所播放的音乐远远超过了19世纪留声机播放的刺耳声音一样，现代概率理论也缩短并简化了伯诺利大量定律的证明。尽管一系列的进步表明了托马斯·爱迪生的原始作品的年龄，但我们仍然对他有很多尊重。同样，我们还应该给予伯诺利对他的金定理的尊重。

“数学中的事情：巨大的问题和非凡的人”

作者：威廉·邓纳姆（William Dunham），[美国]

出版商：人们的帖子和电信出版社

出版时间：2022-03