【源头活水】斐波那契数列——数学海洋中的璀璨明珠
教育,教师的“来源”,跑步“生活”高中教育,重点是刺激教师内的驱动力。 Leshan 1号中学努力建立一个和谐的教学和研究团队,创造强烈的教学和研究氛围,并探索围绕“ Lide Shuren”的教学改革和教育模型,许多杰出的教师以及教学和研究成果已经出现了。

胡瑞(Hu Rui)毕业于东北师范大学,莱桑市(Leshan City)的新秀新秀,以及莱舍(Leshan)第一中学的杰出共产党成员。
一个例子比十个定理更有效。
- hu Rui
fibonacci编号列
- 数学海洋中的明亮珍珠
自然的自然综合是数学的美吗?还是数学揭示自然法则并变得美丽?今天,我将带您进入斐波那契和他的故事。
这个故事的主角意大利数学家莱昂纳多佛比诺像官出生于官方官员家族。从很小的时候开始,东方和阿拉伯的许多城市都逐渐学习并熟练地掌握了印度 - 阿拉比亚的十进制系统,尤其是使用符号0。广泛而深入的研究和研究使他精通各种算术技能,使他在算术,代数和几何学方面做出了许多贡献,并最终成为统治中世纪的主要数学家之一。

但是当时,意大利仍然使用罗马数字进行运营。斐波那尼斯注意到这个美丽而简洁的印度 - 阿拉伯数字计算系统的价值,并积极提倡和使用。
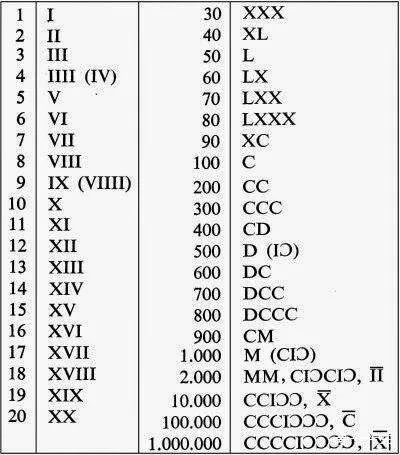
(罗马数字比较表)
01
兔子问题的“奇迹”
斐波那契大约在1202年左右写了一本书《教师书》,该书是一本广泛的博客工具书,显示了如何使用印度 - 阿拉伯数字,以及如何将其用于加法,减法和计算和解决问题。该书记录了一个有趣的数学问题,兔子育种问题。
斐波那契在1202年1202年由意大利数学家莱昂纳多·斐波那纳(Leonado fibonache)排名。为了纪念他,人们称这一数量的斐波那契。要了解此专栏,我们可以这样描述:
假设有一对新生兔子,雌性和雄性兔子各有一只。一个月后,兔子可以繁殖。还假定从第二个月开始,他们可以每月繁殖一对新兔子,这也是男性和女性。如果每对兔子都以上述方式繁殖,那么一对新生的小兔子就是兔子。一开始,50个月后多少对兔子?
使用树图指示兔子的繁殖过程::
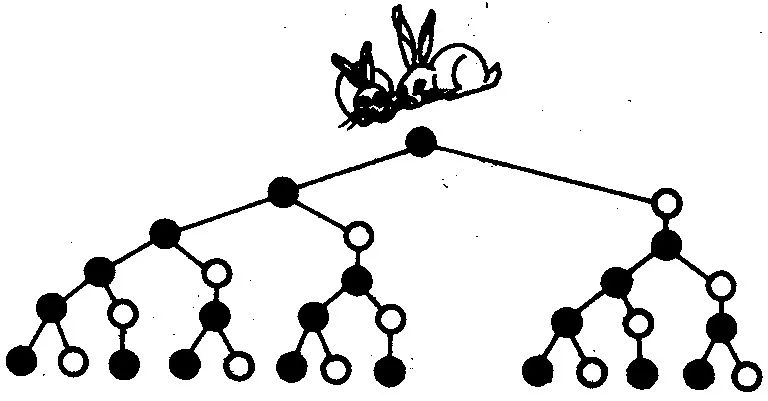
(○:指示新生儿的一对兔子●:一对表示成熟的兔子)
时间
(月亮)
新生兔子
(正确的)
成熟的兔子
(正确的)
兔子总数
(正确的)
13
13
21
13
21
34
10
21
34
55
可以看出,从第一个月开始,每月兔子总数为:
1,1,2,3,5,8,13,13,21,34,55,89,144,233,...
你找到这个法律吗?
斐波那契配额来自第三个项目。每个项目等于前两个项目的总和:
1,1,2,3,5,8,13,21,34,55,89,144,...
该数字以公式表示:
FN = FN-1+FN-2(n≥3)
这个数字有通用公式吗?如何找到列的一般公式?取出笔纸,挑战自己!
斐波那契的引文只是“书”中的一个心理培训主题,没有得到足够的关注。直到19世纪,法国数学家E. Lucas出版了一本关于娱乐数学的四册书。在第一次时,斐波那契的名称被排名。
02
广阔世界的“巧合”
伽利略说:“自然界中的书籍是用数学写的。”。徘徊在野外,抬头看着星空,停止郊区,我们会发现斐波那契的人物无处不在。

向日葵的花瓣以两个方向排列,朝着螺旋方向生长的花瓣数和朝相反方向的花瓣数几乎总是斐波那契数中的两个相邻数字。


松树的松果,水果尺度的排列是螺旋的,每条线上的果实尺度构成了斐波那酸数,而某些花的花瓣数也构成了斐波那契数中的一串数字:兰花花瓣。 ),桃花花(5瓣),Feiyancao(8花瓣),Wanshouju(13花瓣),Ziyuan(21花瓣)等,完全与斐波那契等级的数学定律完全一致,我们完全满是有足够的。大自然现象的美好现象与纤维纳在一起的原因。
03
受设计启发的“来源”
在深度研究中发现,斐波那契和黄金部门比完美完全融合。斐波那契号:1,1,1,1,2,3,5,8,8,8,13,21,34,55,89,....一个比率:
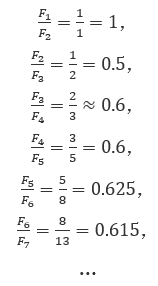
两个相邻数字的比率大于或小于黄金比率
这个比率是无线与黄金比率的,也就是说

(建筑中的黄金比率)

(艺术设计中的徽标)
苹果的徽标不仅仅是被咬住的苹果。圆弧和数学线同时包含数学的严格性和逻辑。 Bonaci被评为其核心基础。
斐波那契号似乎是普通的,但这太神奇了。它从“兔子繁殖问题”中抽象出来,生活中的许多问题反映了其强烈的活力。
04
观看知识的“灯塔”
数学教科书中的“阅读和思考”材料有助于我们了解数学科学与人类发展之间的相互作用,寻求数学发展的历史轨迹,并传达人们对数学文化的教育的价值。
fibonacci引用的公式:
1843年,数学家binet给出了这个公式,该公式显示了数学和整数之间的巧妙联系。
尽管此内容不在大学入学考试检查的范围内,但斐波那契引号的检查主要反映在递归的核心思想中。斐波那契配额的检查是以下模拟测试问题:
意大利数学家Leonardo Fibonacher是第一个研究印度理论 - 阿拉伯数学的欧洲人。斐波那契号被称为最美丽的列。 fibonacci排名{an}满意度:a1 = 1,a2 = 1,an-1+an-2(n≥3开yun体育app入口登录开yun体育官网入口登录app,n∈N+)。如果列的每个项目都放置在网格中,则每个小网格的边缘长度为1,并且上一项占用的网格面积为SN。以下结论是正确的()
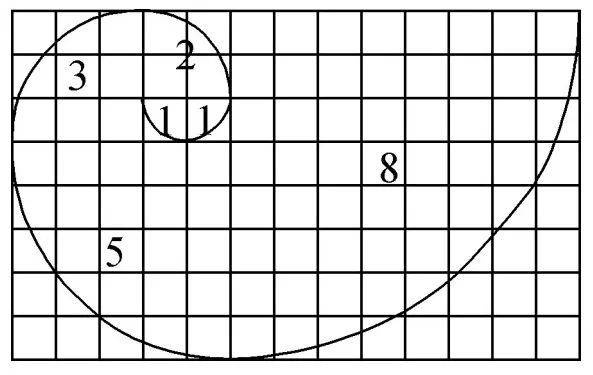
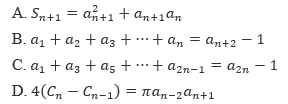
这个问题被列为斐波那契的背景,检查阅读理解和数字的能力,许多学生都害怕。
根据fibonacci编号列的定义开元ky888棋牌官方版,我们可以知道与IS相关的递归公式
an = an-1+an-2(n≥3,n∈N+),
AN+1 = AN+AN 1(N≥2,N∈N+)和
An+2 = an+1+an(n∈N+),
因此,请考虑以下内容:
①通过AN+1 = AN+AN-1(n∈N,n∈N+)获得AN = AN+1-nan-1(n≥2)
所以
sn = a1+a2+⋯+an = a1+(a3-a1)+(a4-a2)+⋯+(an+1-nan-1)
=(a1+a3+a4+...+an+1) - (a1+a2+a3+⋯+an-1)= an+an+an+1-a2 = an+2-1
②来自A1+A3+A5+⋯+A2N-1 = A1+(A4-A2)+(A6-A4)+⋯+(A2-A2N-2)= A2N
以同样的方式,您可以获得A2+A4+A6+...+A2N = A2N+1-1(读者可以自己证明这一点)
③从an = an+1-nan-1(n≥2)和a1 = a2,然后a12 = a2a1
A22 = A2(A3-A1)= A2A3-A2A1
A32 = A3(A4-A2)= A3A4-A3A2
割草
AN2 = AN(AN+1-NAN-1)= ANAN+1-NAN-NAN-1
所以,
A12+A22+A32+...+AN2 = AN+1AN
结合上诉分析,选择正确的答案并不难。
05
数学遗产的“启蒙”
斐波那契报价中有许多有趣的属性。它已在现实生活中广泛使用,例如现代物理,准晶体结构,化学,股票市场分析,生物进化研究和机械结构稳定性。美国还以1963年的“斐波那契季节”的名义发表了一本数学杂志,该杂志用于专门为此列表发表研究论文。但这也有一些未解决的谜团。例如:
有无限数量的纤维纤维吗?
斐波那契数中有多少个完美的数字?
斐波那酸数中有多少个正方形?
割草
斐波那契系列不仅在象牙塔中看着我们。相反,它不仅与大自然结合在一起,而且与我们的生产和生活有着密切的联系。当您凝视fibona时,它也会盯着您周围的您!
Wen tu |胡雷
编辑|周李
评论| Shuai Peilin






