高中数学文化鉴赏专题汇总:斐波那契数列
关键词:纯粹的思想开yun体育官网入口登录app,稳定的情绪,适度的运动,刺激潜力,保持节奏,始终小心,相信自己。可以在公共帐户中搜索高中入学考试最后一课的更多特殊讲座,其中有100多篇文章。
斐波那契配额也被称为金段系列,因为猫。引入了Leonardoda fibonacci作为兔育种的一个例子,因此也称为“兔子柱”。著名的意大利数学家,最重要的成就是找到一组可以描述自然比例的数字0、1、1、2、5、13、21、34、55、89 ...前两个数字的数量等于后者的数量,例如1+1 = 2; 2+3 = 5; 5+8 = 13。同时,不考虑配额中的前几个数字。如果数字删除一个数字,则将获得0.618。如果您使用某个数字在其之后删除第二个数字,则将获得0,例如34 /89 = 0.382。这是我们通常称为黄金分段点的内容。实际上,早在2000年前,“老子”以为“道尚是二,二,两生,三,三,三人和事物”,“ dao”是“丈夫的生活与自然”,所以,道教,道教是自然的。 “这些节目之间有微妙的联系。

以下部分是从Cai Tian的新书《数学与艺术》中选择的,江苏人的出版社
斐波那契
Fibonacci(大约1175-1250)出生于比萨饼,他的真名Filius Bonacci,意为Ponacon的儿子。斐波那契之后的名字在1838年被意大利语(Libri,1803- 1869年)缩写。Liberi是一位伯爵和数学爱好者,以他的爱和窃取古代珍贵手稿的书籍而闻名。
*在Libri担任法国图书馆检查员时,他偷了很多古书籍。当他被发现时,他逃到了英国,里面载着18个大盒子和30,000本书和手稿。他在法国被判处10年监禁;他去世后返回了一些被盗的作品,但仍然有很多失踪。
不仅如此,斐波那契数与Pythagras学校的黄金分割率也密切相关。简而言之,当数字趋于无限时,上一项的极限是后一个值的限制是黄金分割比。除了在数字理论和许多其他数学分支中看到,此序列还经常用于现代物理学,准晶体结构和库存分析的领域。设计问题。

斐波那契雕像(1863年,比萨营)
斐波那纳富含家庭。他的父亲是巴萨共和国的政府官员。他被送往布吉(现为阿尔及利亚)担任商业代理商。 Fibona在童年时代跟随他的父亲到北非,在那里他学习了印度阿拉伯数字。后来,他和父亲一起去了叙利亚,拜占庭(希腊),西西里岛和普罗旺斯。通过广泛和深入研究和研究,他掌握了数学方面的各种技能,尤其是计算。
在12世纪末,斐波那契回到了比萨,并度过了四分之一世纪。他在他的家乡说,并在书中使用印度阿拉伯数字写作来促进欧洲这种数字系统的普及。该数字和计算使用巴比伦人发明的60个防护措施。同时,他还在商业活动的各个领域应用数学。斐波那契还解释了许多代数和几何问题。重要的成就主要体现在不规则分析和理论领域,远远超出了前辈。
大约在1225年,斐波那契被神圣罗马皇帝弗雷德里克二世召唤,并成为一名数学家。据说,皇帝的追随者向他提出了数学问题,并一一回答了他们。皇帝喜欢战斗,美丽,诗歌和数学。他是欧洲弗雷德里克二世的众多君主之一。尽管不是最著名的人,但他有多个国王。该命令是国王西西里岛(1197-),德意志国王(1212-),神圣罗马皇帝(1220-)和耶路撒冷国王(1229-)。
弗雷德里克二世宫殿自然有很多地方。个人推测斐波那契住在西西里王国,这是弗雷德里克二世在童年时代度过的地方。尽管国王有许多国家(例如日耳曼语)的血统,但他并不真正喜欢德国人。 1224年,弗雷德里克二世(Frederick II)在西西里王国(1978年被任命为弗雷德里克二世的大学)创立了欧洲第一所国立大学。它最杰出的毕业生是哲学家托马斯·阿库伊·托马斯·阿奎那(Thomas Akui Thomas Aquinas)(大约1225-1274)。实际上,当时在南部的意大利,那不勒斯王国和西西里王国团结一致。
说到天主教世界最重要的哲学家托马斯·阿奎纳(Thomas Aquina),他比斐波那契年轻。 1225年,当斐波那契被国王弗雷德里克二世召唤时,他出生于那不勒斯的洛卡萨城堡,这是他家人的领土。 16岁那年,他进入了那不勒斯大学,后来在巴黎大学获得了神学博士学位。阿奎娜(Aquina)的杰作是“神学”,它是为了讨论天主教的所有教义。此外,他还给出了五个证明上帝的证据。托马斯·阿奎那(Thomas Aquina)将合理性引入了神学,并宣称:“没有感觉就无法获得智慧。”
至于斐波那蒂是否留在那不勒斯,我们不知道。弗雷德里克二世(Frederick II)忙于战斗,并且教皇有强烈的控制愿望之间的矛盾,斐波那契不太可能在国王的宫殿里呆太久。实际上,在1240年,在他的家乡的一份文件中,他写道,因为斐波那契曾经告诉公民和官员有关计算方法的信息,所以他每年给他几枚金币。换句话说,他可能会在自己的家乡度过自己的年龄,并在那里死去。
斐波那契有五件作品,包括“花”,“找到书籍”,“电影书籍”,“电影书籍”,“实用的几何”和“给帝国哲学哲学家Dowandorus”。 “ Flower”专门针对弗雷德里克二世(Frederick II),这本书包括法庭上的数学竞赛。例如,次级方程式
解决方案。他还证明,三个时间方程式既没有整数或理性解决方案,也没有欧洲几英里的不合理解决方案,即用统治者和循环规则制成的根。但是他在小数点后得到了一个大概的解决方案,没有人知道他是如何得到结果的。
当然,斐波那契最著名的书是“闪光书”(1202)。这里的算盘是指用于计算的沙桌,而不是真正的算盘。本书中引入了分数中间的爆炸“ - ”,这是我们到目前为止仍在使用的符号。还有一个类似于“一百只鸡问题”的不规则方程,该方程应受中国古代数学的影响。这种影响可能通过阿拉伯人的作品传递。此外,他还描述了Fangen的方法和比例转化。但是,最有趣和最重要的是“兔子问题”。
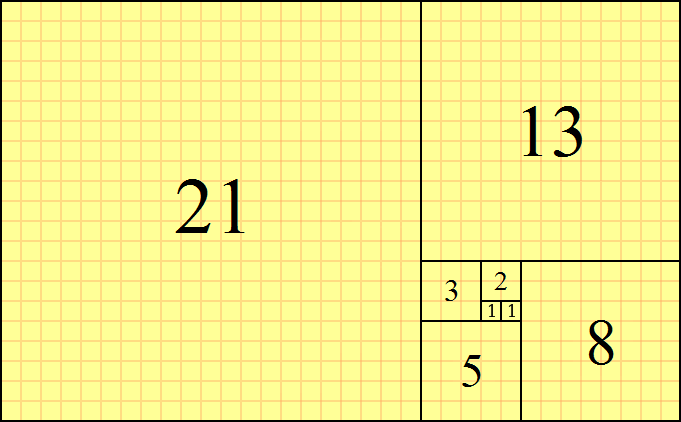
侧长是斐波那契号的平方折叠
一百个鸡肉问题和兔子问题
所谓的“一百个鸡肉问题”出现在北部和南朝。在北魏朝的张Qiujian(也称为Zhang Qiu jian)的《张Qiu jian的计算》一书中,这本书写在公元466 - 485年之间。这片土地已经蔓延到今天。当时,北魏王朝的首都在潘昌(山东,山西),而统治者则是江人。尽管日本古老的首都以及六世纪至八世纪的六世纪开yunapp体育官网入口下载手机版,但平珍(NARA)是在长汉建造的,但其名称应与平昌有关。
Zhang Qiu的家乡位于青还县(现为Xingtai City,Hebei)。他的计算中的最后一个问题是一个亮点,通常称为“一百只鸡问题”。原始文本如下:
今天,有一只鸡,直笔钱五;鸡和儿子,直笔钱三;鸡小鸡三,直笔钱。每个人都买了一百只鸡,问鸡,母亲和小鸡吗?
这意味着公鸡为每钱五美元,母鸡的每钱是三美元,而小鸡只有一笔钱。假设有一百美元,购买一百只鸡(必须使用钱),然后询问多少个公鸡,母鸡和小鸡?
设计用于购买的公鸡,母鸡和小鸡的数量分别为X,Y和Z。
在张Qiujian时代,中国没有引入字母,也没有未知的概念。用文字描述这种方程并不容易。但是,张Qiujian正确地给出了所有三组答案,即(4、18、78),(8、11、81)和(12、4、84)。实际上,通过消除元素,他将这两个三元方程式变成了两个元方程,也就是说
依次以X到4的倍数,也就是说,可以回答以上三组。
如此被称为“兔子问题”是:一对兔子开元ky888棋牌官网版,一年后你能繁殖兔子多少钱?这表明每对兔子每月可以产生一对兔子,每对兔子可以成为一只大兔子,可以在两个月内繁殖。根据“兔子问题”,很容易获得所谓的斐波那契或纤维纳。前十名是:
1,1,2,3,5,8,8,13,21,34,55 ...
该序列的递归公式(数学家发现和定义的第一个递归公式)是
有趣的是,这个数字的一般项目是不合理的。先前由上一个项目组成的数量具有限制,并且该限制正是美学中非常重要的黄金分割比。然而,直到1611年四个世纪,德国天文学家和数学家约翰内斯·开普勒(Johannes Kepler)(1571-1630)才发现了这一限制,并发现他推测限制是古希腊毕达哥拉斯学校的定义。黄金分区比率,即
至于这一限制的证明,在19世纪,法国数学家Jacqtes Binet(1786-1856)给出了它。
在“经典经典理论的几个问题”的英文版本中,序言的插图严格按照斐波那契编号进行排列,即第1页上的两个插图,每个插图,每2、3、5、8和13每个都有一个插图。在本质上,斐波那契数也出乎意料。以植物世界为例,许多花朵的花瓣数正是纤维的数量。例如,李子花5花瓣,飞燕麦8花瓣,13个wanshouju的花瓣,21个紫色花园的花瓣,而雏菊则是34、55或89或89,花瓣都是。

照片由Flash Dantz Onusplash
此外,还有一个有趣的攀登楼梯的例子。假设您可以一步一步迈出一步,也可以逐步登上两个步骤。有几种方法可以爬上N台阶?

比较上类型的定义和斐波那契号列及其初始值,您可以获得
斐波那契有许多有趣的属性,它也有一些未解决的谜团。例如,
有无限数量的纤维纤维吗?
从斐波那契留下的肖像来看,他的魅力很像拉斐尔(Raphael),这是他三个世纪以来的同胞画家。斐波那契经常使用旅行者保持自己。人们喜欢称他为“ Pisa的Lorirad”,并将“ Mona Lisa”的作者称为“ Vinci's Leirado”。我们可以说,斐波那契不仅是欧洲数学复兴的先驱,而且还是东方之间数学交流的桥梁。
1963年,一群热衷于研究世界各国“兔子问题”的数学家建立了一个国际斐波那契协会,并开始在美国发布斐波那契季刊。数学论文与契据数量有关。同时,两年曾在全球举行了斐波那契系列赛及其申请国际会议。这也是世界数学历史上的奇迹或神话。
相比之下,“一百只鸡问题”只是一个孤立的主要数字理论,并且没有可持续研究的内容。
然而,南部歌曲王朝的数学家秦吉沙奥(1202-1261)比斐波那契晚20年,已经扩大了4世纪的“未知”问题“ sun tzu”,该问题推论了中国剩余的中国定理。到目前为止,该定理仍然广泛用于许多数学领域。它已包含在东部和西部的每个主要教科书理论中,根据国际实践,应称为QIN JIU SHAO定理。在2021年出版的“现代经典经典理论的现代指导”(中文和英语)中,我们首先将其命名为Qin Jiushao的定理。

江苏中学的田济州中学的斐波那契序列
斐波那契螺旋线的神奇点是,这种螺旋存在于我们的本性中,分布在大自然的各个方面,让我们看一些图片以欣赏它们的美丽。
(1)海螺中的纤维螺旋线

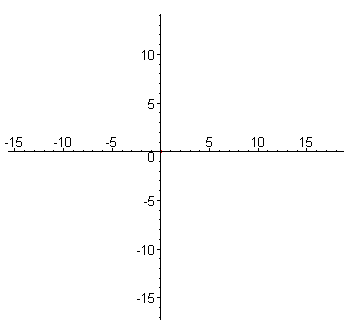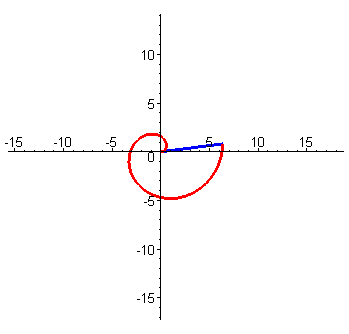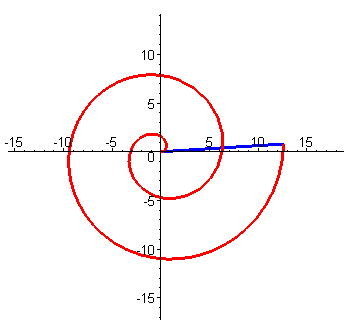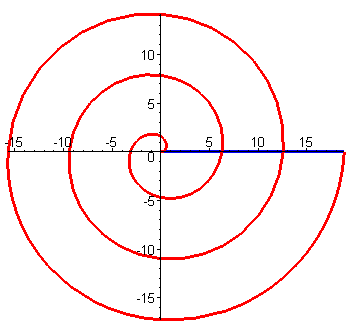

(2)松木中的纤维螺旋线

(3)耳朵中的纤维螺旋线
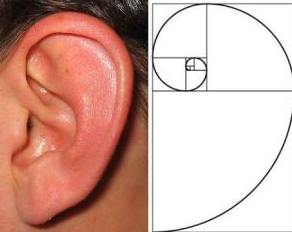
(4)台风中的斐波那契螺旋线
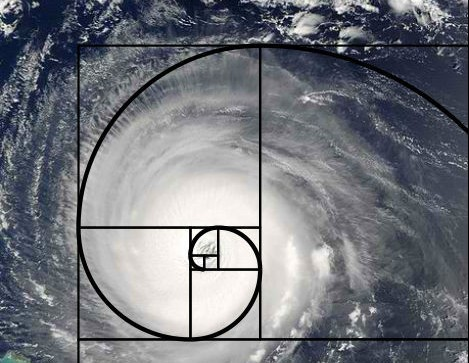
(5)银河系中的纤维螺旋线

斐波那契螺旋线本质上是如此广泛。它必须具有内部谜团。这是自然选择的结果。
在现实生活中,许多设计师的设计灵感也来自于此。例如,Apple的徽标,很少有公司可以使用公司名称进行徽标,而无需确定公司名称。苹果的徽标已经做到了这一点,并已成为世界上最著名的公司徽标之一。徽标具有完美的平衡,映射到徽标的轮廓是直径中斐波那契数的圆形形状。让我们享受:
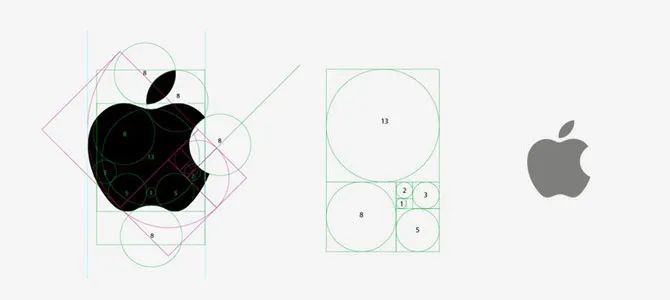


图中的两种葵花籽
有13个绿色计数器线程线程
蓝色顺时针蜗牛线中有21个
13和21是fibonacci编号列中的两个相邻项目
虽然不同的向日葵品种
这些冲击螺旋的数量不是固定的,但通常不会超过
13和21、34、55、55、89或89和144
每组数字是fibonacci编号列中的两个相邻数字
避开,反向螺旋的布置的目的
允许植物使用阳光并最大的空气






