勾股定理归纳总结
一。知识点摘要
1。毕达哥拉斯定理
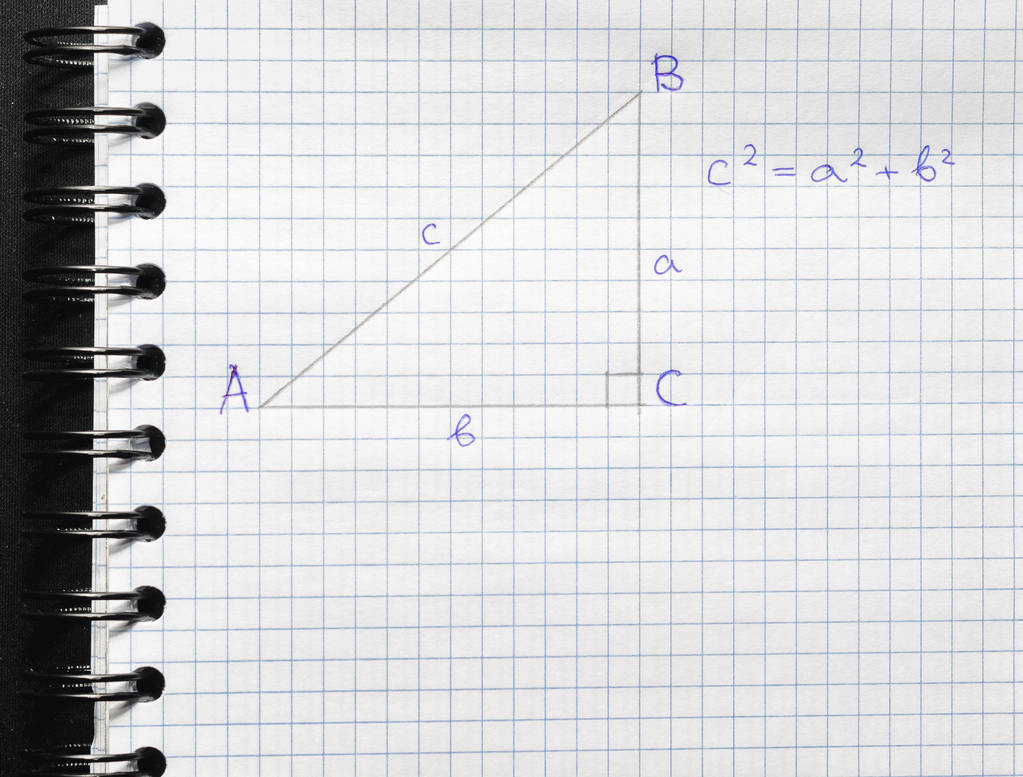
内容:右三角形的两个右边的正方形等于斜边的平方。
表示方法:如果右三角形的两个右角为a和b,并且倾斜的侧面为C,则A2 + B2 = C2。
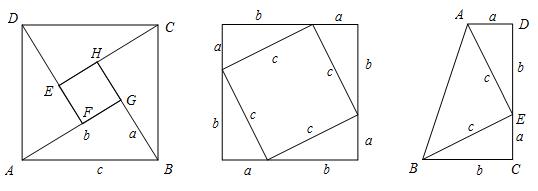
2。毕达哥拉斯定理的证明
有很多方法可以证明毕达哥拉斯定理,常见方法是难题:
3。毕达哥拉斯定理的应用范围
毕达哥拉斯定理揭示了右三角形的三个边之间的定量关系,仅适用于右三角形。
4。毕达哥拉斯定理的应用
①众所周知,右角三角形的任何两个侧面很长,而第三侧很长。
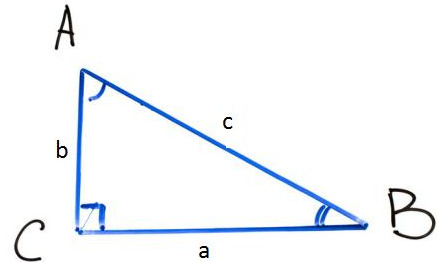
在RTABC中,∂C= 90°,然后有
②如果您知道正确的三角形的一侧,则可以在其他两个方面之间获得定量关系;
③您可以使用毕达哥拉斯定理来解决一些实际问题。
5。毕达哥拉斯定理的逆定理
如果三角形的三个侧面长A,B,C满足A2 + B2 = C2,则此三角形是一个右角三角形,其中C是斜边。
①毕达哥拉斯定理的逆定理是确定三角形是否是右角三角形的重要方法。
它通过“将数字转换为形状”来确定三角形的可能形状,
使用此定理时,您可以将两个小侧的正方形A2 + B2与较长侧的正方形C2进行比较:
如果它们是相等的,则a,b和c是三角形,三个边为直角;
如果a2 + b2 <c2,则带有a,b和c的三角形为三个边是钝的三角形;
如果a2 + b2> c2,则带有a,b和c的三角形为三个侧是急性三角形。
②在定理A,B,C和A2 + B2 = C2中只是一种表达形式,不能被认为是唯一的。
如果三角形的三个侧面是a,b,c满足a2 + c2 = b2,则三个带有a,b,c的三角形,因为三个边是右三角形。
但是此时的倾斜边缘是B而不是C。
③描述毕达哥拉斯定理的逆定理时,
不能说斜边的平方等于两个右角的正方形的总和时,这个三角形是一个右角三角形。
6。毕达哥拉斯号码
①可以形成右三角形的三边长度的三个正整数称为毕达哥拉斯数字。
也就是说,当a2 + b2 = c2,a,b,c是正整数,a,b和c被称为一组毕达哥拉数。
②记住普通毕达哥拉斯的数字可以提高解决问题的速度,例如3、4、5; 6、8、10; 5、12、13等;
③使用包含字母的代数公式来表示N组的毕达哥拉斯数:
7。毕达哥拉斯定理及其倒数定理的应用

2。常见问题的摘要
问题类型1:直接测试毕达哥拉斯定理
[示例1]在ABC中,∂C= 90°。
⑴已知AC = 6,BC = 8。找到AB的长度;
⑵已知AB = 17,AC = 15,找到BC的长度。
分析:绘制图形并直接应用毕达哥拉斯定理以解决问题。
问题类型2:使用毕达哥拉斯定理建立方程
【示例2】
⑴在ABC中,Ab = 90°,AB = 5 cm开元ky888棋牌官网版,Bc = 3 cm,cd⊥ab为d,然后cd =;
⑵已知右三角形的两个右角的比率为3:4,斜长为15厘米,因此该三角形的面积为;
⑶已知右角三角形的圆周为30厘米,斜长为13厘米,因此该三角形的面积为。
分析:求解右角三角形时,您应该考虑毕达哥拉斯定理,两个右角侧的乘积等于倾斜侧的乘积和高度上方的高度。
有时,方程可以根据毕达哥拉斯定理进行配方。
[示例3]如图所示,在ABC中,∂acb= 90°,∂1=∂2,cd = 1.5,bd = 2.5,找到AC的长度。
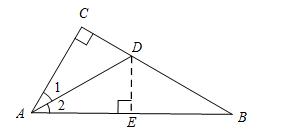
分析:这个问题将毕达哥拉斯定理与一致三角形的知识结合在一起。
分析:令AC = X,Yizhi CD = DE = 1.5,AC = AE = X,
在pythagorean定理中,在rtdeb中,我们可以获得:de2 + be2 = bd2,
也就是说,1.5×1.5 + BE2 = 2.5×2.5,
解决方案为= 2。
根据毕达哥拉斯定理开yun体育app入口登录,在RTACB中,我们可以获得:AC2 + BC2 = AB2,
IE x2 + 4×4 =(x + 2)2,
解决方案是x = 3,
∴AC= 3。
问题类型3:毕达哥拉斯定理在实际问题中的应用
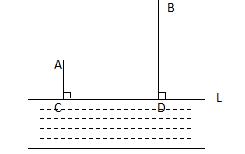
[示例4]如图所示,有两棵树,一棵高8 m,另一棵高2 m。两棵树相距8 m。一只鸟从一棵树的顶部飞到另一棵树的顶部,至少是M飞。
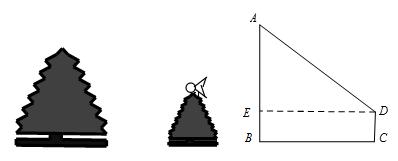
分析:基于问题含义创建数学模型,如图AB = 8 m所示,CD = 2 m,Bc = 8 m,
如果通过点D,则应使用De⊥ab,并且悬挂脚为E,则AE = 6 m,De = 8 m。
在使用毕达哥拉斯定理的rtaed中,我们可以得到广告= 10 m,也就是说,这只鸟至少飞行了10 m。
问题类型4:使用毕达哥拉斯定理逆定理确定三角形是否为右角三角形
[示例5]众所周知,三角形的三个边分别为a,b和c。尝试确定ABC是否是右角三角形。
①a = 1.5,b = 2,c = 2.5;
②a = 5/4,b = 1,c = 2/3。
问题类型5:毕达哥拉斯定理和毕达哥拉斯定理逆定理的全面应用
[示例6]众所周知,在ABC中,AB = 13厘米,BC = 10 cm,BC边缘的中线AD为AD = 12 cm,
证明:AB = AC。
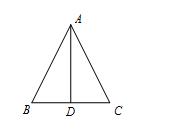
证明:
AD是BC边缘的中心线,BC = 10 cm,
∴bd = dc = 5 cm,
在ADB中,AB = 13厘米,AD = 12厘米,BD = 5 cm,
∵5×5 + 12×12 = 13×13,
∴bd2 + ad2 = ab2,
ADB是一个正确的三角形,
∴ADB=∂Adc= 90°,
∴adb≌adc,(SAS)
∴ab = ac。
3。合并培训
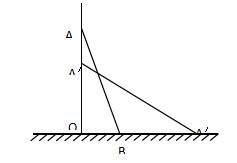
1。正方形梯子长25米开元ky888棋牌官方版,如图所示,靠在墙上,梯子的底部距离墙壁7米,
(1)这个梯子的顶部从地面上有多高?
(2)如果梯子的顶部滑动4米,则水平梯子底部的底部有几米?
(3)当水平滑动的梯子顶部的距离等于梯子底部的距离时,梯子的顶部离地面有多高?
2。如图所示,两个小城镇A和B位于CD的同一侧。河流的距离为AC = 10公里,BD = 30公里。
和CD = 30公里。现在,河流建造了一个水厂,为A和B供水。铺设水管的成本为每公里30,000元。
请选择河CD上的水厂的位置M,以最大程度地铺设水管并找出总成本是什么?