傅立叶变换是如何改变我们生活的？ ——四个角度告诉你答案

介绍：

尽管它没有微积分的声誉和独特的相对性的创新，但傅立叶变革在我们生活的各个方面都悄悄地隐藏在我们生活的各个方面，默默地改变了世界。

对于工程背景的读者而言，傅立叶的第一个分析印象可能是这样：

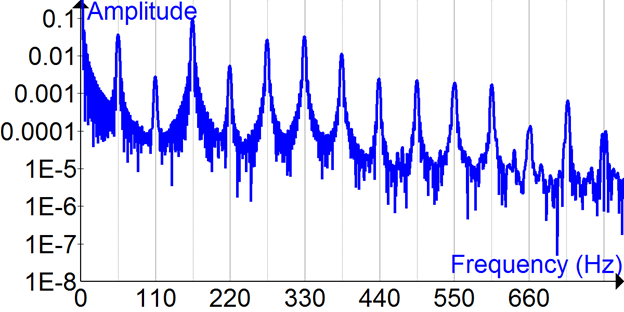
傅立叶变换信号处理的应用之一[1]

在财务分析师的眼中，傅立叶变革就是这样：

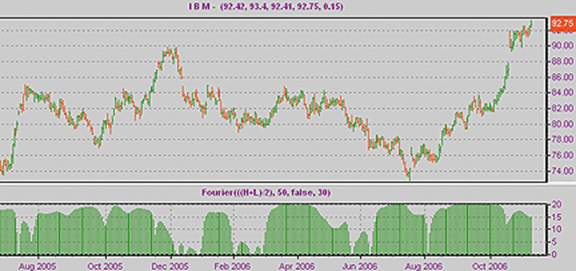
傅立叶变换的第二个应用 - 时间序列分析[2]

在数学家的眼中，傅立叶变革具有七十二个转型，例如魔王：

离散版本的傅立叶变换 - Fourier系列

群体的傅立叶变换 - 连接分析和数量理论的桥梁[3]

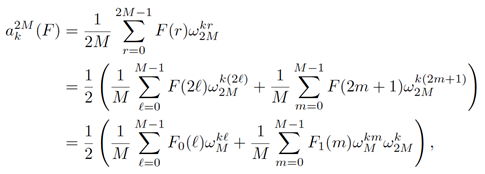
有效的傅立叶变换算法 - 快速傅立叶变换（FFT）[3]

傅立叶分析的进化版本 - 锤子分析。

图显示了利特伍德 - 帕利理论[4]

可以看出，傅立叶变换是理论和应用领域的宝库级工具。实际上，它在信号处理，库存预测，数值模拟，微分方程，数字理论甚至数据压缩中起不可替代的作用。

无论河流有多广阔，它都必须有来源。如果您想对傅立叶变换有深入的了解，则必须从其来源开始。那么谁是傅立叶？

因为“ Fu”也是数百个姓氏之一，所以当我第一次看到傅立叶变革时，我认为这是中国古代的另一本发明。直到我看到Fourier的瞬间面条发型具有中世纪特征和他的毯子般的衣服，我才意识到他不是中国人：

傅立叶。互联网的图片

Fourier（1768-1830）出生于法国，是一位著名的数学家和物理学家[5]。除了傅立叶变换外，著名的热方程（热方程，最简单的扩散方程）也来自傅立叶。一个是积分转换，另一个是微分方程。这两个似乎是无关的，但实际上存在密不可分的联系，读者会在以下文章中理解它们。此外，大气温室效应也是他通过研究热方程的解决方案的第一个发现（当时傅立叶错误地认为海洋也具有像大气这样的温室效应）[6-7]。

现在，我们对傅立叶变换有了初步的了解。那么，它是如何从冷数学概念到“降到地球”到日常生活的呢？考虑到这个问题，我们进入第二部分。

世界上所有的事物都遵循道路，信号处于混乱和搜索周期中

众所周知，诸如阳光，声波和地震波等信号都与不同频率的波（周期功能）混合。

如果书架上的书太多，则必须对它们进行分类。因此，有什么方法可以将这些混乱的信号分类，例如按频率对波进行分类？在数学语言中，给定函数f（x）（x是实际数字），我们可以将f（x）变成与频率k相关的另一个函数

，和

用于代表

各种频率组件的性能呢？这是傅立叶变换的主要任务开元棋官方正版下载开元ky888棋牌官方版，

称呼它

傅立叶变换（在不同地方的定义可能略有不同，但它们本质上是同一件事）：

在实际应用中，我们通常需要一些“良好的属性”，例如正方形集成

所以

和

两者之间满足了parseval的身份。这种身份非常出色，请参考[3]的第三章）。

但是，在理论领域中，这些功能通常不愿“做好”，而傅立叶分析演变为更一般的谐波分析以处理这些不听话功能。

为简单起见，我们首先考虑服从函数（正方形集成函数）。为什么它出现在公式（1）的整体数量下

那项目呢？这个项目中还有一个虚构的符号，看起来像女孩的心一样难以捉摸。实际上，欧拉的身份可以告诉我们答案：

这使得它一目了然 - 正弦和余弦都是周期性的！然后（1）公式必须与周期性有一定的联系！如果读者不相信，以下动画显示出更清楚的

和

两个兄弟之间的关系：

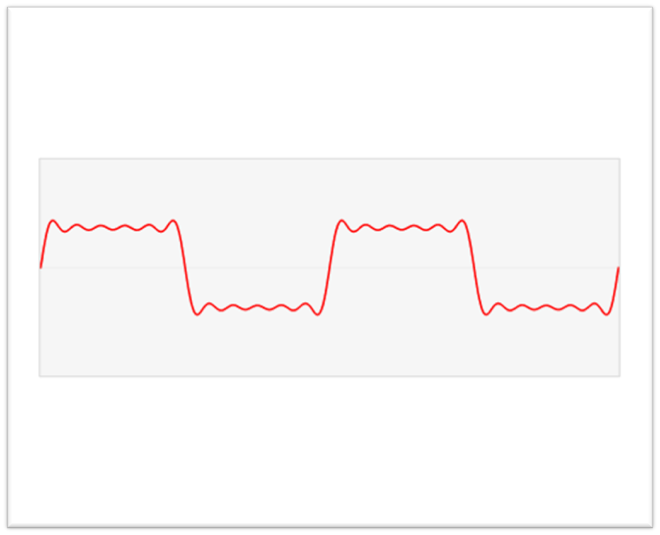
F（x）（红色曲线）分解为不同的频率，然后将这些不同的频率重新组合到

当然，还有许多其他傅立叶变换周期性的应用，下表是一个摘要：

具体示例

傅立叶变换的作用

光谱分析

从本质上讲，它是提取电磁波的频率成分，可以通过傅立叶变换来完成。

时间序列分析

时间序列是与时间相关的随机变量。人们通常会注意这些随机变量之间的相关性。所谓的光谱分析源于此（时间序列“光谱”包含随机变量的相关信息，这与光谱不同。）。光谱分析的关键是时间的傅立叶变换。

CT扫描（X射线）

这种类型的问题是已知波方程的解决方案。您需要倒带并推论原始方程式的外观（也就是说，估计原始方程的参数）。它也称为数学或参数估计问题中的逆问题。 。傅立叶变换在计算中起关键作用。

雷达射程（无线电波）

地震测量（地震波）

差分积分法，FU风格的转换针线

在上一节中，我们知道傅立叶变换如何与周期性或功能频率相关联。实际上，傅立叶变换的另一个重要作用是求解微分方程。傅立叶变换是一个整体变换，如何在差异操作中使用？一切都来自傅立叶变换的重要属性：

在这里，使用了傅立叶变换。大事变成了小事。以上方程式（3）提醒我们，傅立叶变换可以将复杂的偏微分方程转换为简单的普通微分方程，或者它可以将普通微分方程转换为更简单的代数方程！例如，考虑与傅立叶相同的热方程：

通常，转换为普通微分方程就足够了，并且无需进一步转换

解决一阶普通微分方程非常容易。但是不要太早开心，我们得到的解决方案只是

关于x的傅立叶变换

，我必须找到一种方法

恢复它。实际上，我们可以在数学中证明这一点

及其傅立叶变换

有一对一的关系，所以只知道

，解决热方程的解决方案

它即将出来！该结论可以在文件[3]的第4章中找到。

由于其在（3）中（将差速器变成指数）中的出色属性，因此傅立叶变换显示了其在微分方程领域的技能。但是，随着自然科学领域各种问题的复杂性，方程式已经开始变得多样化（例如，主要边界值的差异以及方程系数的平稳性的变化）以及方程解决方案变得越来越奇怪。上面有一些政策和以下对策，并将爆发和解和分析的新兴领域；尽管身份似乎已经改变，但其核心思想仍然是傅立叶的分析。这将在本文第六部分中进一步讨论。

摘要代数显示神秘，分析数字显示力量

我相信读者现在已经学会了傅立叶变换的强大力量：从光谱分析到CT成像，再到微分方程的解决方案，只要它与自然科学相关，傅里叶分析就无处不在。

但这是傅立叶变换的全部力量吗？不！许多人感到惊讶的是，在晦涩的数字理论领域，傅立叶变革也发挥了至关重要而鼓舞人心的作用。

傅立叶变换不是在实数上定义吗？它如何应用于离散的数字理论？这取决于数学家的巨大创造力 - 由于可以在实数上定义傅立叶变换，因此我们还可以在代数组上定义傅立叶变换。

该定义的困难在于，代数组与实数不同。一般而言，前者没有“连续性”的概念（此处不考虑连续性群体），因此该组的傅立叶变换不能通过积分来定义。但是，小组表示理论中的一个重要概念 - 性格（性格）为傅立叶变换的定义铺平了道路。 G组的特征值定义为G：G：

其中“”是指小组中的抽象“多重”操作，而不一定是实数的乘法。

代表一个圆，可以使用

表示（下图是一个示例）。这样，元素a在g中的傅立叶变换为

[3]。

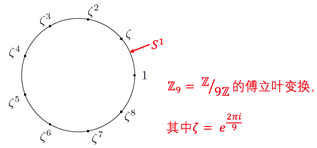
如果我将傅立叶变换移植到这样的抽象代数组，该怎么办？实际上，这个概念在数字理论中可以证明一个非常奇妙而简洁的结论：如果a和d是相互质量的整数，那么序列

其中有无限数量的质数。该结论也称为Dirichlet定理[11]。

具有高级数学背景的读者可能会熟悉“ Dilicre”这个名字。 Dirichlet是一位德国数学家，比傅立叶晚几十年，在分析数理论领域（使用复杂分析方法研究数量理论）做出了许多杰出的贡献[12]。相反，为了证明上述结论，Dirichlet定义了循环组的特殊特征目标（即，正整数的一致类） - Dirichlet特征目标，并使用此功能目标引入L。功能的概念：

通过研究此功能的收敛性，我们可以证明Dirichlet定理。有兴趣的读者可以参考文档[3]的最后一章。

切割甜瓜和蔬菜破裂并将零变成整个极限的可能性

看到傅立叶变换显示了他在工程，微分方程和数字理论等不同领域的技能，统计学家无法坐着：“有没有办法将傅立叶变换应用于概率统计信息？”答案是肯定的，这是概率理论。著名的功能功能。对于实现的随机变量x，概率分布函数为

，其本征函数（傅立叶变换）定义为：

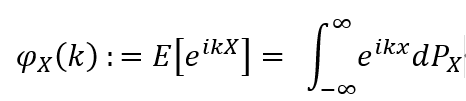
本征函数是概率理论和数学统计中极为强大的工具，并且通过本征函数证明了许多著名的结论。例如，中央限制定理，强大的数字定律等。傅立叶变换可以在概率统计中形成独特学校的原因是，它是由于其其他属性（将两个措施或功能的卷积更改为常规乘法）） ：

在

表达

和

卷积。卷积在概率统计中非常重要 - 假设x和y是独立的随机变量，分别是相应的概率分布函数，那么新的随机变量z的概率分布函数z：= x+y是

。

等等，假设

是n独立的随机变量（不需要相同的分布），然后

分布函数是

。卷积涉及整体操作，这非常麻烦。有没有办法作为一般产品缩写卷积？

也许有些聪明的读者已经看到了

执行傅立叶变换的N功能的乘积不是吗？

这样，

分布函数似乎不那么复杂。这是概率统计领域许多经典结论的本质。

纯理论分析始终是抽象的，所以让我们看看。以中央限制定理为例：

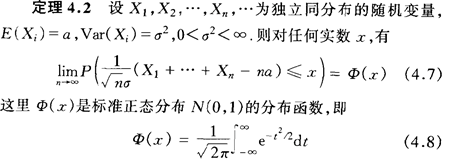
摘自文学[13]

该定理意味着当随机变量的数量增加时，逐渐遵守正态分布。该定理的核心思想是找到特征函数（傅立叶变换），然后证明此特征函数接近正态分布特征函数（可通过Taylor扩展证明）。

在本文的第三部分中，作者提到傅立叶变换是可逆的，因此功能函数可以完全确定概率分布函数。有关特定的证据，请参阅[14]（本书从三级数字定理中得出了更一般的中心限制定理和相关估计，但核心想法都是特征函数）。

不只是传统

到目前为止，傅立叶对这种数学工具的分析无所不在，无所不在且无所不在地对天地，这对许多读者睁开了眼睛。但是，这无法满足数学工人的胃口。上面介绍的大多数内容属于经典类别，而数学的资深驱动力已经熟悉这一点。

但是，对于如此强大的工具开yun体育官网入口登录app，傅立叶的野心不仅限于古典数学。除了上面提到的“元兼容性”外，傅立叶的分析和现代数学也密切相关。例如：

周期性和信号处理：

基于傅立叶变换和功能周期性之间的关系，人们开发了出现的数学领域，例如小波分析和压缩感应。

例如，小波分析本质上是将模拟（连续）或数字（离散）信号从时间和空间域转换为频域以提取信号的频率特征，因此它是信号处理过程的关键。著名的香农采样定理给出了信号的最小采样点的数量与信号频率之间的关系，成为小波分析领域的关键定理。

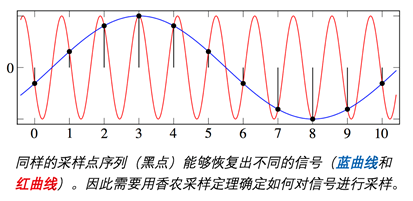
压缩感知是一种信号采样技术，目的是用尽可能少的采样点恢复原始信号。压缩感知诞生于1990年代，其核心算法是套索方法（该方法是由统计学家发明的，可以减少数学模型中的参数数量）。关于压缩感知的最引人注目的是，它充分利用了信号的频率特征，甚至可以突破香农的采样定理中最小采样点的极限[16]。

微分方程的解决方案：

由于傅立叶分析只能处理具有良好属性（例如L²功能）并且无法满足许多实际问题的功能，人们逐渐开发了更强大的武术分析（Harmonic Analysis）。有兴趣的读者可以参考此领域。经典作品[8]。

至于如何将和谐分析应用于微分方程，我们可以参考Miao Changxing教授的两部作品[4]和[9]。谐波分析的最新应用之一是，道Zhexuan在2014年使用了三维纳维尔 - 斯托克斯方程的某些弱版本的解决方案的存在和爆炸（千年的七个主要数学问题之一）[10 10） ]（有限时间爆炸），关键是在傅立叶变换中使用这些想法（特别称为傅立叶乘数，请参阅[8]）。

数字理论和组合：

作者在第五部分结束时提到了L功能的概念。实际上，L功能是分析数理论中的核心问题之一。 Riemann猜想中出现的ZETA函数（千年的另外七个主要数学问题）是L函数的特殊情况。

此外，陶氏族证明了一个结论，即“质数集包含任意长度的算术序列”（称为绿色 - 陶定理），这被认为是促进Dilicre定理的一种。有兴趣的读者可以参考[15]；本文中的一个重要想法是将傅立叶分析的概念应用于拓扑组（组结构和拓扑结构，因此可以使用分析和代数均值进行研究）[17]。作为数学社区中罕见的全能球员，傅立叶的分析可能是陶恩最重要的思想来源。

概率理论：

由于中心限制定理是通过征函数证明的，因此人们感受到了傅立叶分析在概率统计中的神奇效果。

渐近理论的许多结论是概率理论的主要分支，由征本征函数的方法（例如贝里 - 埃森中心限制定理）证明。该定理可以视为中央限制定理的某种加强，因为它在中心极限定理中给出了渐进式正常的速度（随机变量的数量增加，这些变量将这些变量近似于正态分布）。有关具体证明，请参阅[14]。

结论

到目前为止，我们强烈认为傅立叶变换在不同领域具有非凡的价值。最后，为了加深读者的印象，最后，我将总结本文的一般内容：

应用区域

傅立叶变换的特性涉及

频率分析和频谱分析

提取相应函数的频率（周期）信息，或通过函数的频率信息推导原始函数的表达。

微分方程

差异转换为指数，这种转换是可逆的。

数学统计

卷积转化为普通产品，这种转换是可逆的。

分析数理论

将离散代数组转换为连续的复杂平面，并将数字理论问题转换为分析问题。这种转换也是可逆的。

从上面的摘要中不难看出，尽管傅立叶变换的应用程序似乎无关紧要，但实际上它们有一个共同点 - 也就是说，它们都采用了傅立叶变换的可逆性。正是由于这个原因，傅立叶变换是连接各行各业的隐藏主线。表面上很难理解，但实际上是简洁而普遍的。这是数学的魅力和本质。

实际上，存在许多数学积分变换，例如拉普拉斯变换（实际数字的傅立叶变换），希尔伯特变换（将正弦变成余弦，在相位分析中很有用）和更一般的盖尔范·德变换（傅立叶范变换（傅立叶从操作员代数的观点等等。它们在自然科学界是独一无二的，每个社区都具有风格，并且相互关系。因此，只要掌握傅立叶变换的基本思想和特征，其他不可或缺的转换就会成为袋子中的事物。

从19世纪初期的法国诞生到现在，在科学研究界，傅立叶转型仍然是一个非常活跃的话题。也许未来的傅立叶转型将更有用，但这不仅取决于数学家的独特创造力，而且还取决于整个科学界的共同努力和合作。毕竟，科学没有严格的分界线。

尽管有许多分支，但不同的学科却密切相关