🚁pg下载官方网站-pg下载2025最新版本V4.20

初二几何核心包含轴对称与勾股定理呀，这同时也是中考很高频出现的综合考点呐，高效学习的关键存在于“吃透性质、牢记模型、精准应用”之中呦，不需要盲目去刷题就能够稳稳拿到分数哒。 一、轴对称：抓住“性质加上模型”，去破解几何图形题核心必定考点，高效的学法是画图标注要优先：做轴对称题的时候要先画出对称轴，使用不同的...

01技术简介 纳米是个长度单位，1纳米等同于10 -6毫米，这也就等同于人类头发丝直径的六万分之一，纳米技术是近些年迅猛发展起来的一种新兴技术。因其具备诸多的优势而被广泛投用到各自关联项目。制剂技术领域便是其中之一。纳米制剂技术是指借助纳米尺寸，针对药物开展对应加工后再处理，最终转化成不同类别剂型，实现或达成...

周自琴 有一位叫周自琴的人，他具备中学一级教师的身份，是陕西省的教学能手，还是安康市的学科带头人，同时也是平利县 的优秀教师一员，另外是平利县培训团队数学方面的核心成员，也是平利县城关初级中学的数学教研员。 勾股定理，属于八年级数学下册第十七章，它揭示出直角三角形三边关系，体现了那种“形数统一”的思想方法，那...

两千零二十一年相关单位将举办粉体表面改性技术高级研修班并于两千零二十一号的四月二十二日至二十三日在江苏南京举行，报名方式为一八三零一二一六六零一，其适用对象包括非金属矿粉体企业，比如碳酸钙企业、硅微粉企业、滑石企业、重晶石企业、硅灰石企业、高岭土企业、膨润土企业、白云石企业、石灰石企业、硅灰粉企业、云母企业、...

于中考物理所涉的备考进程里，牛顿第一定律绝对是一座务必要去攀登的高峰，它不单单是力学领域的基石，还更是衔接宏观世界跟微观世界去理解的关键桥梁呐。今天呀，那就让我们一块儿去撩开牛顿第一定律的神秘面纱，以生动且有趣的方式，探寻这一物理定律背后所潜藏的奥秘，以及它怎样于我们日常的生活当中发挥重要作用哟。 一、牛顿...

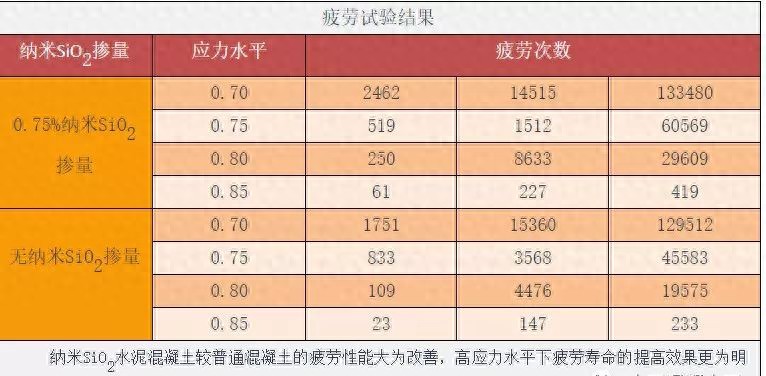
纳米技术，作为前沿技术，在混凝土里的应用，正在蓬勃兴起，已然成为混凝土技术研究领域的一个热点。借助纳米技术以及纳米材料，开发新型的混凝土外加剂，如果增加混凝土外加剂的品种，提高混凝土外加剂的性能，还有对混凝土改性的效果后，还能减少副作用 。 纳米材料可有效改善混凝土的性能 1、纳米二氧化硅 纳米SiO2，是由...

一同启动奇妙的悟理之行，一块儿目睹奇迹的瞬间，物理我最厉害，物理许可证力审纪字第1期，牛顿第一定律，物理学科中心，力与运动同生活紧密相连，怎样阐释以上现象呢？爱因斯坦称：历经数千年，一个因太过复杂而模糊不清的基本问题，便是运动问题。新课导入，我只想安静地待着，瞧我大力创造奇迹，1探索历程，2牛顿第一定律（牛顿...

嘿，大伙好呀pg下载赏金下载pg下载通道，今儿个咱来唠唠数学领域一位“老相识”——勾股定理，好多人兴许在学校学过它，然而究竟是谁率先提出来的呢，它究竟具备啥用途呢，实际上，此定理的历史以及应用都蛮有意思的，咱一块儿瞧瞧。 谁提出这个定理，开篇就遇此问题，着实复杂。不少人讲是古希腊毕达哥拉斯发现，故而称作“毕...

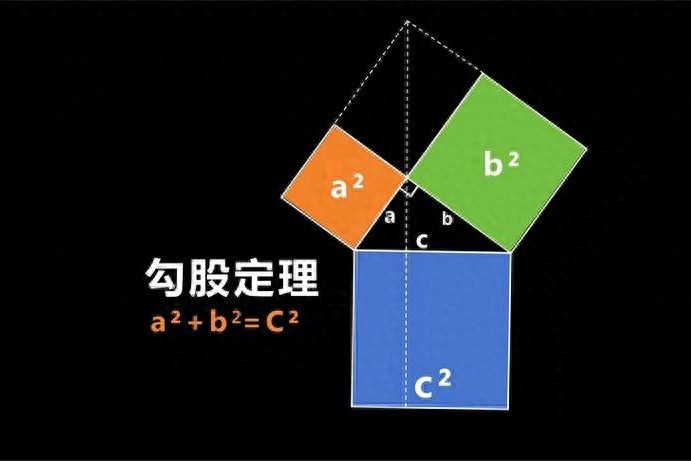
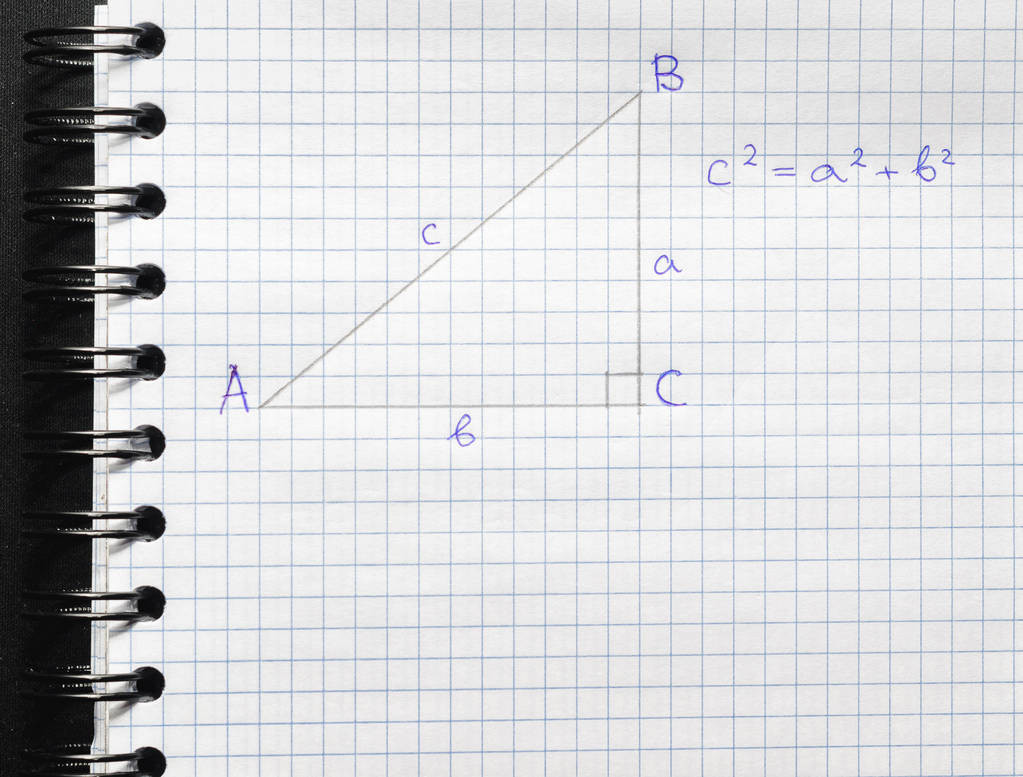
一．知识点归纳总结 １．勾股定理 内容：直角三角形两直角边的平方和等于斜边的平方. 表达形式哦：要是直角三角形之中，两条直角边分别是a与b，而斜边是c，那么a的平方加上b的平方等于c的平方 。 ２.勾股定理的证明 勾股定理的证明方法很多，常见的是拼图的方法： ３.勾股定理的适用范围 勾股定理对直角三角形三...

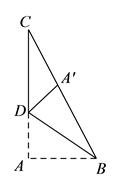
折叠问题，它属中考热点范畴，同时也是难点之所在，一般会跟动点问题相互结合起来呢，而这类问题的题设情况，往往是把某个图形依照一定的条件去进行折叠，之后依据图形折叠前后所产生的变换来分析状况，还要借助轴对称性质以及勾股定理等相关知识去解答哟。 这类问题，其立意有着新颖之处，且是充满变化的，若要解决这类问题，除了需...