pg下载赏金下载 勾股定理归纳总结
一.知识点归纳总结
1.勾股定理
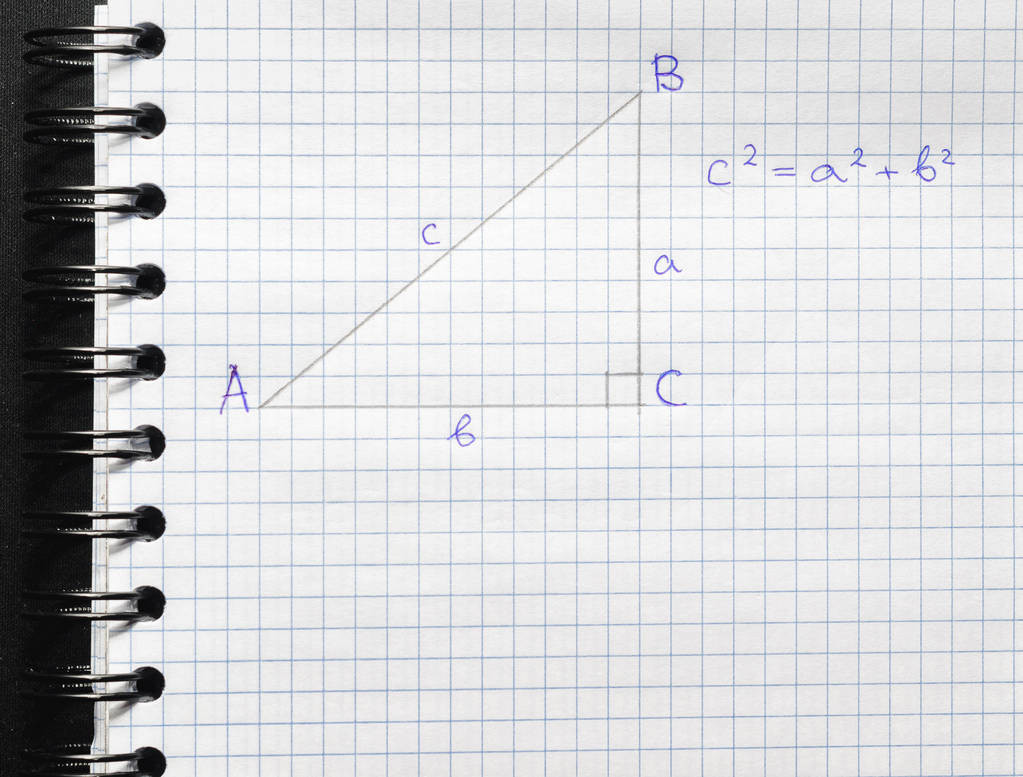
内容:直角三角形两直角边的平方和等于斜边的平方.
表达形式哦:要是直角三角形之中,两条直角边分别是a与b,而斜边是c,那么a的平方加上b的平方等于c的平方 。
2.勾股定理的证明
勾股定理的证明方法很多,常见的是拼图的方法:

3.勾股定理的适用范围
勾股定理对直角三角形三条边之间存在的数量关系予以揭示,它仅仅适用于直角三角形,是这样一种定理 。
4.勾股定理的应用
① 已知直角三角形的任意两边长,求第三边长时;

在 RtABC 中,∠C = 90°,则有
② 知道直角三角形一边,可得另外两边之间的数量关系;
③ 可运用勾股定理解决一些实际问题 .
5.勾股定理的逆定理
要是三角形三边的长度,分别是a、b、c,并且满足a的平方加上b的平方等于c的平方,那么这样的三角形就是直角三角形,而且其中c是斜边 。
判定一个三角形是不是那种直角三角形,勾股定理的逆定理是一种挺重要的方法,。
它通过 “数转化为形” 来确定三角形的可能形状,
于运用此一定理之际,能够用两小边的平方之和 a2 加上 b2,去跟较长边的平方 c2 展开比较 ,。
若它们相等时,以 a,b,c 为三边的三角形是直角三角形;
若 a2 + b2 < c2,时,以 a,b,c 为三边的三角形是钝角三角形;
当出现 a 的平方加上 b 的平方大于 c 的平方这种情况的时候,以 a、b、c 作为三条边所构成的三角形是锐角三角形 。
②定理当中,a,b,c,以及a2 + b2 = c2,仅仅是一种表现形式,千万不能认为它是唯一的,。
如果三角形的三条边的长度分别是a,b,c,并且满足a2 + c2 = b2,那么以a,b,c作为三边的那个三角形是直角三角形。
但此时的斜边是 b 而不是 c 了 .
③勾股定理的逆定理在用问题描述时,
不可以表述成:在斜边的平方等同于两条直角边的平方相加之情况时,此三角形为直角三角形 。
6.勾股数
① 能够构成直角三角形的三边长的三个正整数称为勾股数,
当 a2 + b2 = c2 成立时存在这样的情况,此时如果 a,b,c 均为正整数,那么就称 a,b,c 为一组勾股数 。
记住那些常见的勾股数能够提升解题的速度,比如说3、4、5,6、8、10,5、12、13等等 。
③ 用含字母的代数式表示 n 组勾股数:
7.勾股定理及其逆定理的应用

二、常见题型归纳总结
题型一:直接考查勾股定理
【例题1】在 ABC 中,∠C = 90°.
⑴ 已知 AC = 6,BC = 8.求 AB 的长 ;
⑵ 已知,AB的长度是17,AC的长度是15,那么求BC的长度是多少 。
分析:画出图形直接应用勾股定理即可解题 .
题型二:应用勾股定理建立方程
【例题2】
在三角形ABC里,角ACB是90度,AB的长度是5厘米,BC的长度是3厘米,存在CD垂直于AB且垂足为D,那么CD的长度是多少呢 ;。
(2)已知,直角三角形当中,两直角边的长度之比是3比4,其斜边长15厘米,那么这个三角形的面积是 ;。
Ⅲ 已知,有一个直角三角形,其周长是 30 厘米,斜边的长度为 13 厘米,那么这个三角形的面积是.
剖析:于解直角三角形之际,得去想到勾股定理,以及两直角边相乘所获得的结果会等于斜边跟斜边上高相乘起来的结果 。
有时可根据勾股定理列方程求解 .
试看【例题3】,有这样一幅图,在ABC这个三角形当中,∠ACB的度数是90°,∠1与∠2的度数相等,CD的长度是1.5,BD的长度为2.5,要去求出AC的长度。

分析:此题将勾股定理与全等三角形的知识结合起来 .
进行解析,设定AC的长度为xpg下载网站麻将胡了,很容易知道,CD的长度是1.5 ,DE的长度也是1.5 ,AC的长度等于AE的长度,其长度为x 。
在直角三角形DEB当中,依据勾股定理能够得出,DE的平方加上BE的平方等于BD的平方 。
也就是,一点五乘以一点五,再加上BE的平方,等于二点五乘以二点五 ,。
解得 BE = 2 .
于直角三角形ACB当中,依据勾股定理能够得出,AC的平方加上BC的平方等于AB的平方,。
即 x2 + 4 × 4 = (x + 2)2 ,
解得 x = 3 ,
∴ AC = 3 .
题型三:勾股定理在实际问题中的应用
在【例题4】所呈现的图示里,存在着两棵树,其中一棵的高度是8米,另一棵的高度为2米,这两棵树之间的距离是8米,有一只小鸟从某一棵树顶端的树梢位置飞到了另一棵树顶端对应位置的梢头,那么它至少飞行了米数。

做这样的分析,要依据题意去构建数学模型,呈现出来就是,如图所示,AB的长度是8米,CD的长度是2米,BC的长度是8米 。
过点D作出一条与AB垂直的线,线为DE ,DE与AB相互垂直的情形下拥有的垂足为E,于是就出现了这样的结果也就是AE等于6m ,而DE为8m 。
根据勾股定理,在直角三角形AED当中pg下载麻将胡了,能够得出AD的长度是10米,这也就意味着小鸟最少飞行的距离为10米 。
题型四:应用勾股定理逆定理,判定一个三角形是否是直角三角形
【例题5】已知,三角形的三边长度分别是 a,b,c,试着判断 ABC 是不是直角三角形 。
① a = 1.5,b = 2,c = 2.5 ;
② a = 5/4,b = 1,c = 2/3 .
题型五:勾股定理与勾股定理的逆定理综合应用
在三角形ABC当中,已知AB的长度是13厘米,BC的长度为10厘米,还有BC边上存在一条中线AD,其长度是12厘米,。
求证:AB = AC .

证明:
∵ AD 是 BC 边上的中线,BC = 10 cm ,
∴ BD = DC = 5 cm ,
在ADB里,AB的长度是13厘米,AD 的长度是 12厘米,BD的长度是5厘米,。
∵ 5 × 5 + 12 × 12 = 13 × 13 ,
∴ BD2 + AD2 = AB2 ,
∴ ADB 是直角三角形,
∴ ∠ADB = ∠ADC = 90° ,
∴ ADB ≌ ADC,(SAS)
∴ AB = AC .
三、巩固训练
一个呈现出方形形状的梯子,其长度为二十五米,就如同图示那样,以倾斜的形态靠在一堵墙面之上,而这个呈方形的梯子底部与墙面之间的距离是七米,。
(1)这个梯子的顶端距地面有多高?
(2)要是梯子的顶端向下滑落了 4 米,那梯子的底端于水平方向朝哪个方向滑动了几米、滑动了多少米呢? 。
(3)当,梯子的顶端下滑的距离,跟梯子的底端水平滑动的距离,是相等的时候pg下载,这时,梯子的顶端距地面有多高 ?

2、如图所示,存在A、B两个处于河流CD同一侧的小集镇,它们各自到河的距离分别是,AC等于10千米,BD等于30千米,。
并且,CD 的长度是 30 千米,当下需要是于河边建造一处自来水厂,为 A、B 两镇来供给用水,而铺设水管所产生的费用每千米达 3 万,。
您需在河流CD那儿挑选水厂的位置M,以此让铺设水管所产生的费用最为节省,然后还要算出总费用究竟是多少 ?







