转发到头条
在1202年,斐波那契在Liber Abaci提出了一个问题:假设有一个男性,女性和一只新生兔子,他们将在一个月内成长为大兔子,并在一个月后开始交配。雌性兔子生了另一对兔子,一个月后,它们也开始繁殖,然后继续这样。每只雌性兔子开始繁殖时,每月都会生下一对兔子。假设没有兔子死亡,请问一对新生兔子一年可以繁殖多少对兔子?

没错,这是著名的斐波那契序列的起源。 1月1日,只有一对兔子,下个月,它成长为大兔子并开始繁殖,因此2月只有一对兔子,所以三月份有两对。下个月,新兔子长成一只大兔子,原始兔子生了另一对,所以四月有三对... 21,34,55,89,144,253…。以序列为第13位,这是一年内兔子的总数。
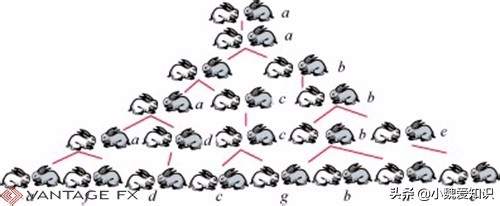
互联网上的图像源,如果删除了任何侵权
从序列中不难看出,从第三项开始,每个项等于前两个项的总和。现在
(n = 3,4,…)。同时开元ky888棋牌官方版,斐波那契序列的一般术语公式
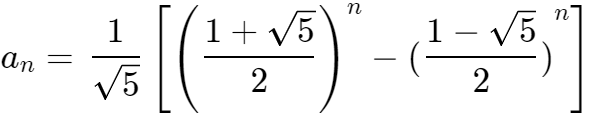
可以在(n = 1,2,3…)中看到一个熟悉的公式:
这不是我们经常在中学中称之为的黄金比例吗?实际上,您可以验证这一数字随着数字的不断增长,上一项在下一个项目的划分中越来越接近0.618。

我曾经以为苹果的徽标非常独特,为什么我被咬了?事实证明,Apple徽标的设计是由圆形切成半径为斐波那契序列(1、1、2、3、5、8、13)的圆圈。 Apple徽标是从图中的辅助线分解的,但实际上,Apple Apple徽标的标记设计并不严格符合黄金比例,但非常接近,这使它变得神秘。
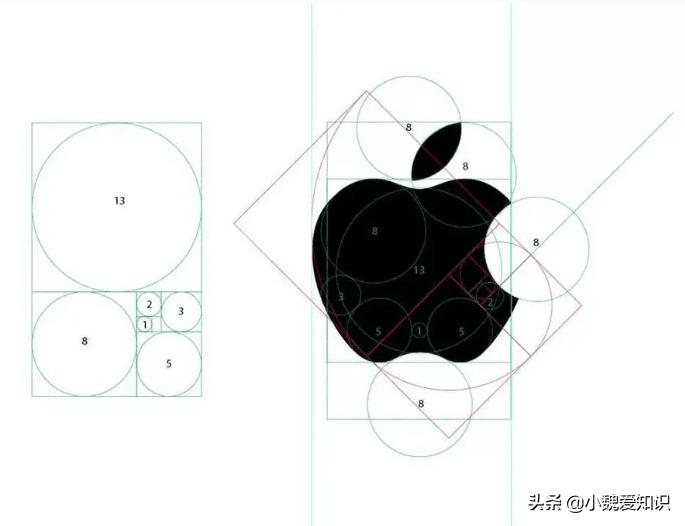
在现实生活中,有许多应用使用斐波那契黄金的美,无论是来自古代和现代建筑,某些贝壳的形状,或者举世闻名的画作“ Mona Lisa”,还是一些植物叶订单...自然,生活,科学和数学的美丽相互伴随。



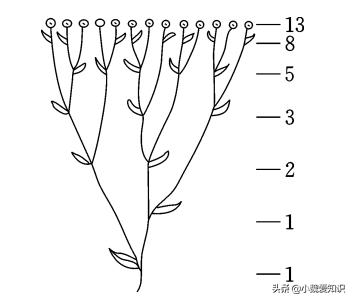
正是由于它的黄金美和广度几乎每次都在数学或计算机算法中谈论。这是一个python代码,它简单地输出斐波那契序列:
def fbnq(n):
fbnq = [1,1]
if n ==1:
fbnq.pop(n)
elif n >= 2:
for i in range(2,n):
fbnq_value = fbnq[i-1] + fbnq[i-2]
fbnq.append(fbnq_value)
else:
print('出错')
for ctn in fbnq:
print(ctn,end=' ')
fbnq(n)当然,在学者中,基于斐波那契算法的应用包括优化算法,搜索算法,识别算法等。其中一个是基于fibonacci的fibonacci树优化算法(FTO),基于fibonacci方法,通过fibonacci方法通过全局搜索,通过全局搜索搜索algorith algorithm搜索方法最佳解决方案广泛用于许多优化问题,例如多峰值功能优化问题,例如区域电网速度调节和数据中心流量调度。
FTO(斐波那契树优化算法)生成一个搜索元素集,也称为芽集,然后根据fibonacci系列生长到fibonacci树中,斐波那契树的每个节点都是搜索元素的最佳解决方案。具体步骤如下:
(有关详细信息,请参见参考文献[4])
我搜索元
搜索元素的产生分为两个阶段:全局搜索和本地搜索:
全局搜索:
全局搜索阶段随机生成全局搜索点G,并初始化搜索元素的第一个列元素。
在本地搜索阶段,在上一列中具有最佳健身价值的元素和新生成的全局点G分别根据上述公式生成新的本地点。
#有关特定步骤[4]请参阅参考文献
II FTO算法步骤
使用全局搜索元素作为芽点来初始化I-The Iteration中的芽点集,从芽点集中取出,并将其计算为FI-1 + FI-2芽点。使用一个芽点使用搜索元素生成算法生成一个新的芽点。在这一轮迭代中,生成FI-1 + FI-2新的芽点以将新的芽点存储到芽点集中。芽点根据堆栈结构的最后一步方法进入堆栈,以确定迭代条件。如果符合问题,则芽点是输出的开元棋官方正版下载,例如,具有最佳健身值的芽点是输出。否则,返回步骤2
然后,进行收敛和时间复杂性分析。 (有关详细信息,请参见参考文献[4])
参考
[1] Zhu Yongsheng。植物和斐波那契数[J]。 Zhenjiang高等教育学院杂志,2006,19(1):67-69。
doi:10.3969/j.issn.1008-8148.2006.01.019。
[2] Sheng Sijia,Zhao Yulin,Li Yingchun。 “斐波那契序列”的美学教学设计[J]。中学数学,2022(1):25-27。
[3] Li Meiling。关于斐波那契序列的有趣讨论[J]。科学技术协会论坛(下半月),2008年(8):42-42。
doi:10.3969/j.issn.1007-3973.2008.08.027。
[4]张·宋海(Zhang Songhai),什叶派(Shi Xinling),李·彭(Li Peng)等。用于多模式函数优化的金段纤维纤维树优化算法[J]。 Acta Electronics开yunapp体育官网入口下载手机版,2017,45(4):791-798。
doi:10.3969/j.issn.0372-2112。
[5]中国百科全书中国百科全书委员会编辑委员会编辑委员会,中国百科全书·生物学[/],北京:中国百科全书出版社,1992年




