“养正”第一课丨从勾股定理谈起
最近,我在家乡建造的杨山幼儿园已经完成。应该使用哪种形式的仪式?在考虑了很长一段时间之后,我们决定庆祝课堂上的完成。



其中一个是数学课,我特别邀请了我的第二个叔叔。他今年今年75岁,一生都是数学老师。我的第二任叔叔启发了我的数学。当时,我的第二位叔叔用树枝写着并在田野里绘画,教我最初的数学知识,包括毕达哥拉斯定理。


第二叔叔潘·舒林(Pan Shulin)上了“生存”的第一堂课

在这个公开班上,ER叔叔谈到了使他着迷的毕达哥拉斯定理。我编译了他的课件并与您分享:
您好,同学!您好,亲爱的客人!
我今天要解释的话题是:从毕达哥拉斯定理开始。今天,我将与您一起欣赏毕达哥拉斯定理背后的悠久历史及其直至今天的影响力。
1。毕达哥拉斯定理的历史从发现到证明
从历史的角度来看,在毕达哥拉斯学校严格证明了毕达哥拉斯定理之前,许多古代文明已经应用了毕达哥拉斯定理,或者已经知道一些典型的毕达哥拉斯人。
公元前2000年左右。在当时的美索不达米亚地区(在今天的伊拉克)中,出现了一个具有光荣历史的古老文明:巴比伦。

耶鲁大学巴比伦收藏YBC 7289系列
耶鲁大学的巴比伦馆有一个粘土板编号的YBC7289,该木板将正方形分为四个小角三角形,并以楔形形状雕刻一些古老的角色。经过现代古语言学家的解释,事实证明,正方形的对角线与侧面长度的比率大约等于1.414213(√2准确至第六个小数点)。

哥伦比亚大学Plinton Pavilion 322 Collection 15组毕达哥拉斯
哥伦比亚大学普林顿馆(Plinton Pavilion)的第322号系列也是粘土板。解释结果是15组毕达哥拉斯的数字,满足:前两个整数的平方之和等于第三个整数的平方。
古埃及的地理位置距离古代巴比伦的地理位置不远,两个主要文明在生存时代也有交叉点。那古埃及人是否知道他们是否知道毕达哥拉斯定理?
除了建造金字塔的宏伟项目外,古埃及的城市废墟还显示出非常复杂且规则的模式。哈希姆(Hashem)是《科学故事》一书的作者,曾经断言埃及人必须使用该公式A² +b²=c²,否则他们将无法建造金字塔。
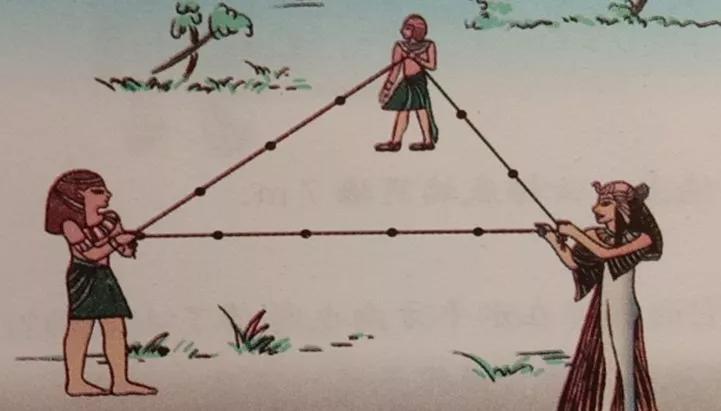
古埃及人的绳索绘画艺术想象
古埃及人确实让我们留下了拉绳以形成右三角形的传说:在绳索上相等的间隔13节,一个人握住两端并将它们固定在一起,另外两个人分别保持了第四节。打结8,然后拉直,这是一个正确的三角形。显然,这是右三角形,上面有“钩子三,大腿四和和弦五”。

兰德·帕普鲁斯(Rand Papyrus)的三角记录
大英博物馆保存了一些记录古埃及文明的纸莎草纸(也称为土地纸莎草纸),其中一些三角形记录已经存在。
古代印度文明也是人类最古老的文明之一。在古印度有一本书,名为“《佛经》(The Sutra),该书是在公元前公元前公元前5世纪写的。它主要谈论祭坛的建筑技术,其中包含一些几何知识。这本书表明,到那时他们已经知道毕达哥拉斯定理,并使用了3.09的piπ。古代印度也有一个数学经典,称为“圣使的收藏”,该数学记录了66个有关数学的内容,包括算术操作,乘法,正方形开口以及代数,几何学和三角学规则。
上面提到了三种古代文明 - 古巴伦,古埃及和古印度 - 人们对毕达哥拉斯定理的理解和应用。接下来,我们应该谈论我们的中国文明!

“ zhoubeng jing”
在“千钟”中,有一个记录:在与周朝的数学家尚高的周冈的对话中,提到:大腿被栽培,大腿被栽培,大腿被栽培,大腿被栽培,大腿被栽培,大腿被栽培,大腿是五个。”它被翻译为:当右三角形的两个右角挂在三个右侧时,链为四个,斜直径角(和弦)为五个。后来,人们只是简单地称其为“钩三弦四弦五”。
“ Zhoubeng Jing”写在公元前100年左右。该书使用毕达哥拉斯技术来计算天体运动的数量,并且有句话:“八英尺的表面是大腿,表面阴影是钩子。”尽管没有提供毕达哥拉斯定理的证据,但毕达哥拉斯定理的应用仍然非常深入。
《周概》摘要还记录了陈Zi(公元前7世纪至公元前7世纪)的一段话:“如果您寻求邪恶的阳光,您应该将太阳带到下面的太阳,因为钩子和太阳高,而毕达哥拉斯人将是互相乘以彼此,并使用处方消除它,而邪恶将在一天的结束中。”显然,Chen Zi不再限于“钩子三,四和五”的特殊情况,而是在谈论右三角三角之间的一般关系。
毕达哥拉斯定理是我国家所说的。在西方开元棋官方正版下载,该定理称为毕达哥拉斯定理。因为毕达哥拉斯是第一个严格证明毕达哥拉斯定理的人。

毕达哥拉斯,古希腊数学家
在公元前六世纪,古希腊数学家毕达哥拉斯(Pythagoras)证明了毕达哥拉斯定理:在右角三角形的飞机中,两个右角的长度的正方形总和等于倾斜侧的长度正方形。为了庆祝,毕达哥拉斯学校屠杀了100头母牛,祝贺。因此,该定理也称为一百个牛定理。
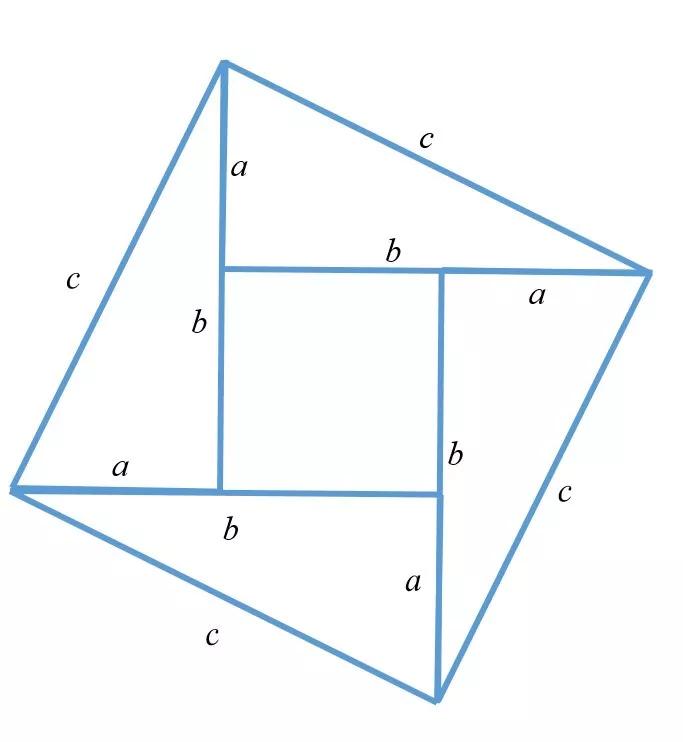
Zhao Shuangxian图验证方法
我国家最早证明毕达哥拉斯定理的人是三个王国时期(约182---250)的吴王国的数学家赵肖。 Zhao Shuang创建了一个“毕达哥拉斯圆形方形图”,该图证明了毕达哥拉斯定理的证明,基于一个相当于四个一致的直接三角形和小正方形面积的大正方形的总和。
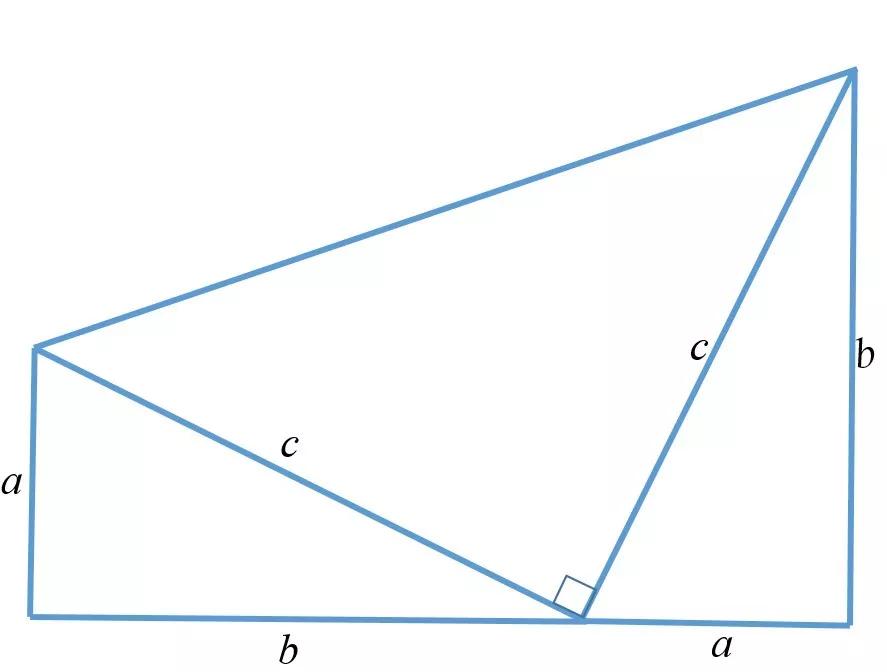
加菲尔德证明
美国第20任总统加菲尔德(Garfield)还提供了毕达哥拉斯定理的证明,这是非常简洁,清晰,流行且易于理解的。这种证明方法的想法是,使用两个一致的右三角形和一个等同代右三角形来形成梯形,并通过面积计算获得毕达哥拉斯定理。
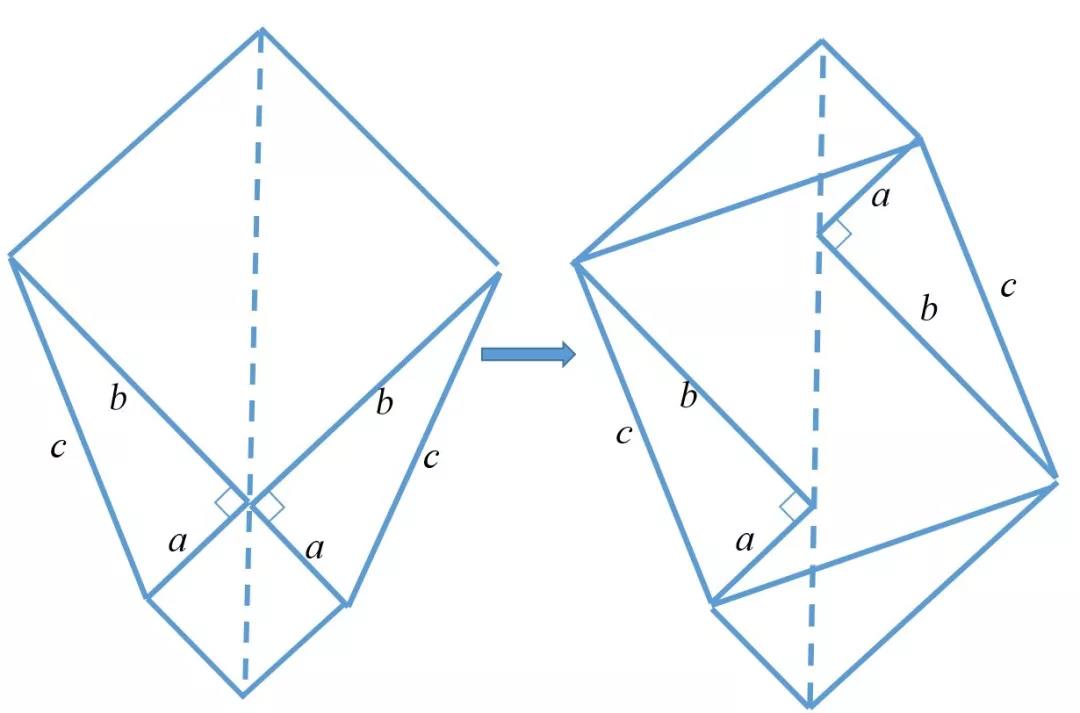
莱昂纳多·达芬奇的测试
莱昂纳多·达·芬奇(Leonardo da Vinci)还提供了毕达哥拉斯定理的证明。他用两张相同的纸拼出不同的空隙,两个空隙的区域相等。他用来证明毕达哥拉斯定理以找到两个空隙区域的平等性。
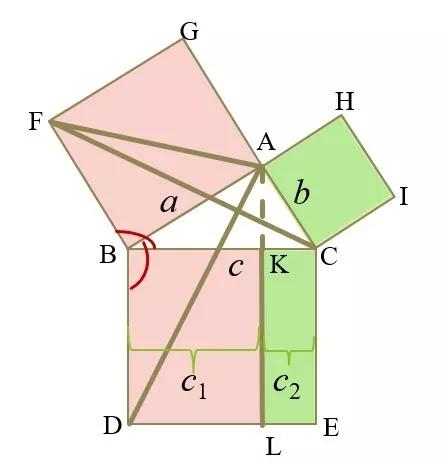
“原始几何”的命题47卷1-最经典的证明
今天,当时我们再也找不到毕达哥拉斯的证明了。我们可以从Euclid的“几何来源”中找到最经典的证据(摘自第47章,第1卷,“几何的起源”)。欧几里得比毕达哥拉斯晚约200至300年。他的方法是利用一致三角形的判决定理来证明毕达哥拉斯定理。
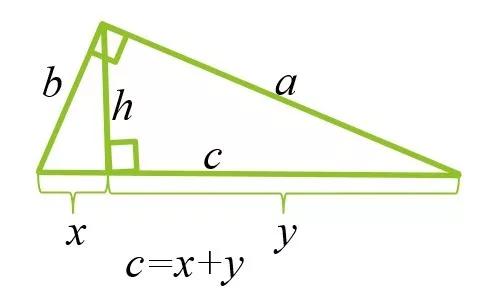
命题31,“原始几何”的第6卷 - 爱因斯坦证明与之相似
据说爱因斯坦在十二岁时也有证据,但后来发现这实际上不是原始证据,而是来自第31期的“原始几何”第6卷。但是他对Bi's的早期痴迷定理允许爱因斯坦在十年后取得成果:Bi的定理以四维形式出现在他的相对论特殊理论中,并发挥了关键作用。后来,在相对论的一般理论中,出现了扩展形式。


有关毕达哥拉斯定理证明方法的书籍
迄今为止,已经提出了400多种毕达哥拉斯定理的证据。数学的魅力不仅是猜想的证据,而且是向已知定理提出新证明的挑战。在中世纪,如果学生想获得数学学位,他们需要提出毕达哥拉斯定理的原始新证明。在我的国家恢复大学入学考试之后,1979年大学入学考试中的数学问题之一是证明毕达哥拉斯定理。据说只有1%的候选人正确回答了这个问题。
2。导致第一次数学危机
我报告的第二部分是:第一次数学危机,这一危机的根源在于毕达哥拉斯定理。
毕达哥拉斯学校的哲学是“一切都计算”。思考:
宇宙的和谐在数字上
上帝通过数字定律创造世界
世界上的一切都可以是数字和数字的比率
(除了理性数字)世界上没有其他数字

河马,毕达哥拉斯学校的门徒
公元前500年,毕达哥拉斯学校的门徒希帕斯斯发现,带有两个右角的三角形的长度为1(即,我们所说的今天√2)不是一个合理的数字。这与Bishi学校的“一切都是数字”(理性数字)的理念大不相同。 Passos被监禁,以各种方式遭受酷刑,最后被沉没的船执行。
然后√2是什么?
①这是同步右三角形的倾斜长度,长度为1。
②它是正方形的对角线长度与侧面长度的比率
它的算术特征也可以汇总到以下两个方面:
①不能表示为两个整数的比率
②是无限的非循环小数
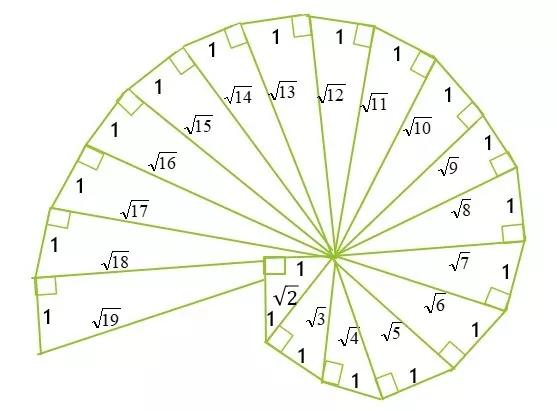
从N-1的平方根制成N的平方根
人们进一步发现,根据毕达哥拉斯定理,根据此基础,以√3,...,√n长度为基础的线段很容易。除了仅遇到平方数n,它不能表示为两个整数的比例,而是无限的非环状小数。
今天,我们知道这些数字被称为非理性数字。可以在任意两个有理数之间插入无限多个非理性数字,并且可以在任何两个非理性数字之间插入无限多个有理数。

德国数学家Dedekin
关于非理性数字的研究和讨论持续了超过2,000年。直到19世纪,德国数学家Dedekin才给出了一个非理性数字系统的定义,该系统结束了由非理性数字引起的第一次数学危机。
毕达哥拉斯定理也与另一个众所周知的非理性数字(即PI)的计算密切相关。尽管人们很早就意识到π的存在,但直到1761年,瑞士科学家兰伯特才证明π是一个不合理的数字。
Archimedes的PI计算方法
古希腊的阿基米德首先提出了一种可以使用数学过程来准确测量π值对任何准确性的方法:一个圆的周长必须大于内联规则多边形的周长,并且小于切线的常规多边形。周长。根据这一原则,可以不断提高PI的近似计算的准确性。
Archimedes使用常规的96面形状获得:PI的近似值在3.1408和3.1429之间。当他发现多边形的长度时,他反复使用了毕达哥拉斯定理。
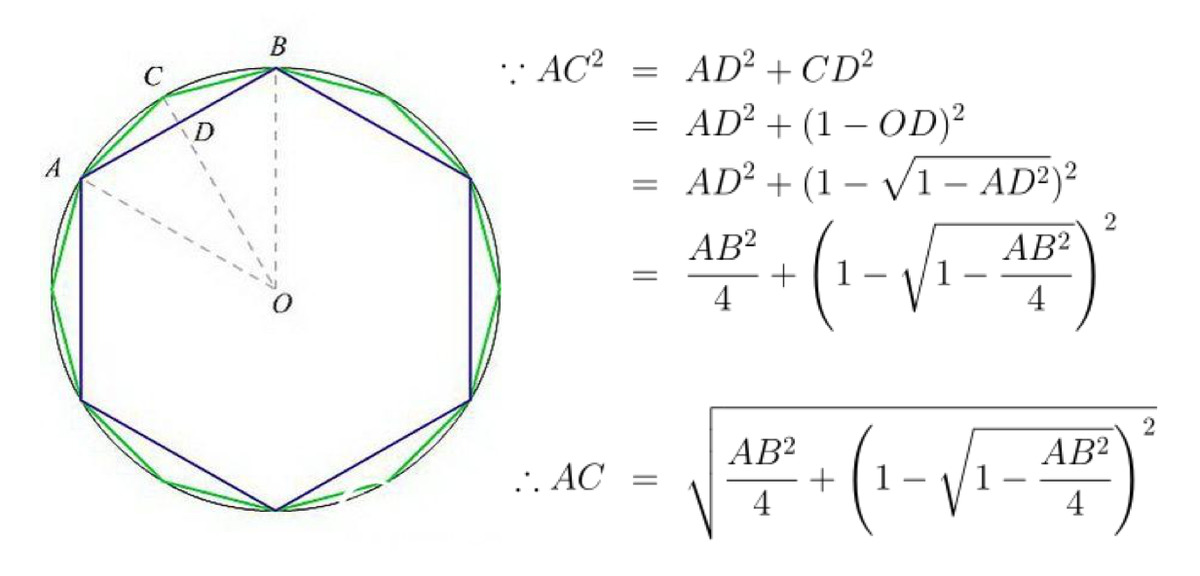
包皮环切切割技术背后的毕达哥拉斯定理
我国魏(Wei)和金王朝(Jin dynasties)的数学家刘hui(Liu Hui)也提出了一种计算PI的近似值的方法,即割礼的艺术。这个想法是使用单位圆的区域近似Pi。它背后的数学原理是毕达哥拉斯定理。 。
通过使用Pythagorean定理两次,您可以建立一个迭代公式,如上图所示:从侧面长度AB侧长度AB在圆圈中连接的圆中,您可以计算侧面长度AC的侧面长度AC圆圈连接在2N侧的圆圈。反复迭代,当有足够的侧面时,圆圈中常规多边形的面积不断接近PI。
Liu Hui将圆切成常规的3072边缘开yun体育官网入口登录app,并找到:π≈3.1416。在南部和北部的王朝期间,数学家Zu Chongzhi进一步将圆切成一个正24576的一侧,以找到:3.1415926 <π <3.1415927。该结果比西方领先近1000年。
简而言之,从毕达哥拉斯定理到第一次数学危机的出现,再到对非理性数字的讨论,这是一个漫长而艰巨的故事。
3。建造数字和形状的桥梁
毕达哥拉斯定理描绘了飞机上右角三角形三个边的长度之间的关系。经过进一步的思考,我们发现它与15世纪出现的平面矩形坐标系具有许多相似之处:如果将两个直角侧延伸到两侧,因为带有方向的直线记录为X轴和Y轴,则然后矩形顶点是坐标原点O。这不是平面矩形坐标系吗?目前,两个右角是从斜面到X轴和Y轴的投影。

法国物理学家,数学家和哲学家笛卡尔
传说是笛卡尔的灵感来自悬挂在墙角的蜘蛛网,并提出了一个平面矩形坐标系。
使用平面矩形坐标系,我们可以轻松地计算平面上任意两个点之间的距离。假设平面上两个点的平面坐标分别为(x1开yunapp体育官网入口下载手机版,y1)和(x2,y2)。他们每个人都会垂直于X轴和Y轴,在连接这两个点后,如图所示,获得了一个右角三角形。根据毕达哥拉斯定理,很容易获得这两个点之间的距离公式。
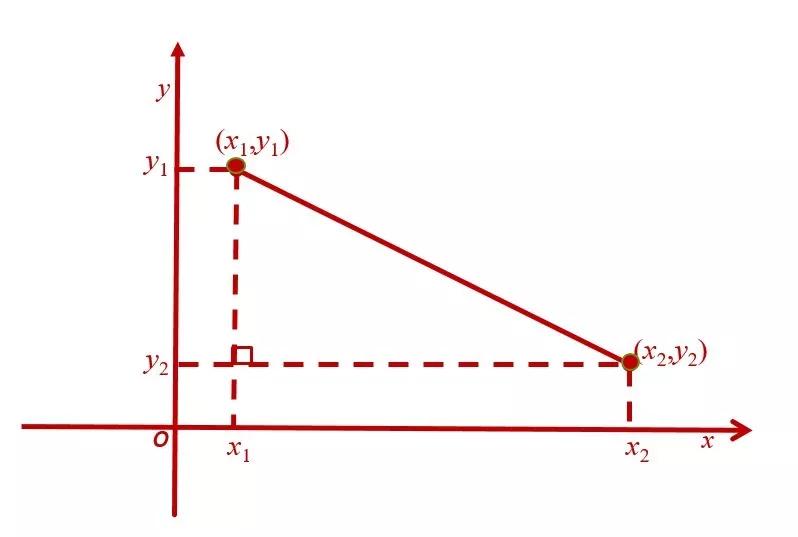
飞机上两个点之间的距离公式
二维平面上两个点之间的距离公式也很容易推广到三维空间,而其背后的数学原理仍然是毕达哥拉斯定理。
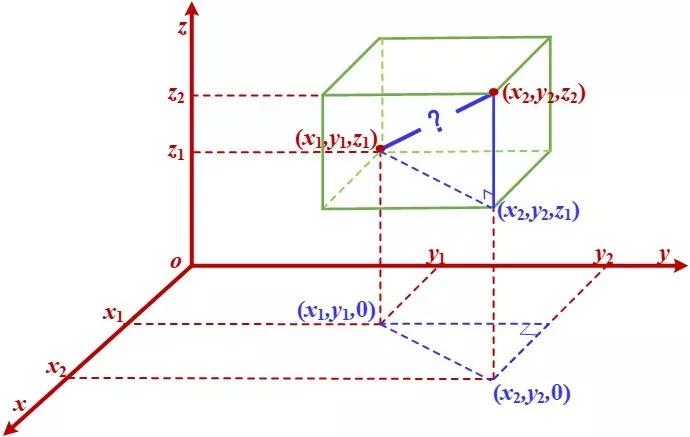
三维空间中两个点之间的距离公式
矩形坐标系的创建允许通过代数方法解决几何问题。从那时起,分析的几何形状就诞生了,为建立微积分奠定了基础,从而开辟了一个可变数学的广泛领域。
毕达哥拉斯定理是连接数学数字和形状的第一个定理,建立坐标系统使数字和形状不可分割。
4。挑衅FEMA的猜想及其证明
与毕达哥拉斯定理密切相关的另一个概念是所谓的毕达哥拉斯数,这是满足A2+B2 = C2的三个正整数。例如,(3,4,5)和(5,12,13)都是毕达哥拉斯的数字。那么有多少群毕达哥拉斯人?今天我们已经知道:有一组无限的毕达哥拉斯数字。但是,在远古时代,找到毕达哥拉斯的数字是非凡的。

法国数学家FEMA
1637年左右,法国数学家费尔玛(Ferma)想到了一个看起来与毕达哥拉斯人数量非常相似的问题:是否有三个积极的整数满足A3+B3 = C3?此外,是否有满足a4+b4 = c4的正整数(a,b,c),或更一般而言an+bn = cn(n> 2)?
我们不妨先尝试A3+B3 = C3的情况。每个立方体数对应于正立方体的体积。您不妨尝试使用“移动砖”的想法,以查看是否可以将两个正立方体移动并堆放到另一个立方体中?
以侧长6和8(63 = 216; 83 = 512)为例,以正长为例,我们发现这些“砖”被堆积在侧面长度9(93 = 729)的正立方体中,并且缺少一块。改变。无论您如何移动,它都无法正常工作。那么,这是不可能的吗?
费马特(Fermat)当时是否做过许多徒劳的尝试将砖头移回去?所有子孙后代都可以知道的是这个故事:Fermat在《古希腊数学家Diophantu》一书“算术”页面的边缘上写道:“将一个立方数分为两个立方数字的总和,或者将四立方数分为两个立方数字,或者将四次数字划分为四次动力。两个能力的总和超过两个相同力量的总和,这是不可能的。这太小了,无法写下来。”
这是著名的fermat猜想,也就是说,当n> 2,xn+yn = zn不过是零整数解决方案。
Fermat提出的问题和猜想的起点是,它使许多伟大的数学家陷入困境,并在358年中挑战了后来的几代人!它的证明过程是数学史,它产生了许多新的数学思想和方法。

Fermat大定理证明的历史年代学
在这里,我们列出了Fermat定理的证明历史记录。可以说,星星闪闪发光!许多伟大的数学家证明了Fermat定理的一些特殊案例。
自从费玛(Ferma)于1637年至1839年提出了Ferma猜想以来,整整200年:Euler证明了N = 3的状况,Lejeander证明了N = 5的情况,Ram证明了N = 7的情况。证明了n = 14的情况。
每个数学家的名字都是众所周知的,但他们只能回答一个相对较小的n的fermat猜想的特殊情况。
直到1850年,库默证明了一组fermat猜想的案例:对于3到100,除了3个特殊数字外,Fermat猜想在其他情况下是有效的。
大约100年后,人类进入了电子计算机时代,而Fermat猜想的验证也进入了计算机验证的时代。 1987年,格兰维尔(Grandville)使用计算机将n从3亿至1亿验证,而费马特(Fermat)的猜想是有效的。
但是,我们知道,无论验证了多少索引n,都无法取代理论证明。追求Fermat定理的严格理论证明仍然是许多一流的数学家的梦想。
最终,在1995年,威尔斯证明了费马特的猜想对所有正整数n超过2!
1993年6月,安德鲁·威尔斯(Andrew Wiles)在英格兰剑桥大学发表了一系列报道。报告标题没有引入关注,论证过程是冗长且非常熟练的。但是在第三次演讲后20分钟,他低估了五个符号:“ => flt”。含义是:我以前的证据推论了费玛特的宏伟定理(也称为Fermat的最后定理)。

英国数学家威尔斯
这一事件立即震惊了整个数学社区,而威尔斯闻名了一段时间。威尔斯随后向世界上最高的数学期刊Mathematicae提交了200页的证明。杂志编辑部已安排了6位顶级数学家来执行手稿审查任务。其中,一位名叫卡兹(Katz)的审稿人在证明中发现了一个逻辑缺陷。
起初,威尔斯认为缺陷很容易解决。但是,当他着手解决缺陷时,很长一段时间都没有进步。直到1994年9月,在他的学生泰勒(Taylor)的帮助下,威尔斯才解决了证明中的脆弱性。 1995年5月,威尔斯(Wiles)在《国际顶级数学年度》(Top International Journal)年度年度中发表了一系列证明所有作品的证明,并提供了最终的证明,并随附了多达130页的讨论。

威尔斯于1995年发布了完整证书
1998年,威尔斯(Wiles)因这项杰出工作而获得了田野特别奖。
为什么威尔斯如此成功?也许答案是四个词:永远不要忘记您的最初意图!威尔斯10岁时对Fermat的定理感兴趣!在他证明了Fermat的定理之后,他说:“……没有其他问题对我来说与Fermat的定理相同。我在成年后的生活中有一种罕见的特权。我的童年梦想……那个特别而漫长的梦想探索已经结束,我的心平静下来。”
回顾过去,让我们考虑一下费马特(Fermat)在1637年做出猜测时说的话:“我敢肯定我发现了一种很棒的证明方法,但不幸的是,这里的空白太小了,无法写下来。”
有人必须问:Fermat说他没有写的证据是否有可能是威尔斯的证据?唯一合理的答案是“否”。威尔斯使用了最新的数学工具和思想来证明费马特的大定理,这些定理比费马特时代晚了。大多数数学家认为,Fermat的经过验证的方法很可能是错误的,但他只是让自己感到困惑。
Wu Jun曾经评估过Fermat在“数学通用知识的50次讲座”中的宏伟定理证明:“该定理本身的证明过程导致了许多数学研究结果的出现,尤其是椭圆方程的研究。今天,区块链,区块链技术使用椭圆加密方法是基于它的。”

日本数学家Toshiya Taniyama
Fermat定理的证明过程诞生了椭圆曲线理论:在1950年代,日本数学家Taniyama和其他人建立了椭圆曲线和模块化曲线之间的关系,该曲线证明了“ Fermat的定理”一步;但是,在1958年,在1958年,在1958年,在1958年,不到31岁的Gu Shanfeng选择自杀。 1985年,密码学家Neal Koblitz和Victor Miller独立提出了椭圆曲线密码学。如今,椭圆曲线加密已成为基于比特币等区块链技术的加密货币的基本数学基础。

自从比特币的发明者萨托西·纳卡本(Satoshi Nakamoto)尚未表现出他的真实面孔以来,每个人都猜到了萨托西(Satoshi)提出比特币的意识形态动机。纽约州立大学的计算机科学系终身教授Gu Xianfeng曾在一篇文章中说:“关于比特币数学原理的简短讨论”:“旧的GU一直倾向于相信Satoshi Nakamoto发明了他对塔尼·亚马苏(Tani Yamatsu)硬币的敬意。疯了
谢谢大家!
【主要参考材料】
1。Limaor,由Lin Yanquan等人翻译:“ BI的定理:四千年”,Sanmin Book Company,2017年
2。WuJun的“关于数学常识的50次讲座”
3。由西蒙·辛格(Simon Singer)撰写,由Xue Mi翻译:“费马特定理 - 一个谜,使世界智慧混淆了358年”,广西师范大学出版社,2013年
4。由Sheng Liren和其他人编辑,“从毕达哥拉斯定理开始”,中国科学技术大学出版社,2012年。
5。朱利安·哈维尔(Julian Havil
6。Baidu百科全书
7.彼得·布朗(Peter Brown),由潘·莱(Pan Lei)翻译:“数学最著名的证据几乎是如何破裂”



