在日常生活中,伯努利方程有哪些应用场景?
大家好,今天我们将谈论伯努利方程。
Bernoulli方程是物理和工程学中一个简单但极为重要的方程式,可以帮助我们深入了解广阔世界中流体的流动行为。本质上,该方程描述了流体流体中压力,速度和高度之间的关系。

Bernoulli方程式是什么?
例如,Bernoulli方程在工程方面有许多应用程序,可以用来解释飞机如何产生升降机?或计算从容器中流出的液体的速度,等等。
在探索这些应用程序之前,让我们看一下Bernoulli方程式是什么?它由瑞士物理学家丹尼尔·伯诺利(Daniel Bernoulli)于1738年出版。方程式的表达如下。方程式左侧的三个术语的总和沿流线保持不变,它们的尺寸都是压力。该术语是静压,这是我们经常称为流体压力P的术语;第二项是动态压力,它是流体密度ρ和速度V的函数,代表单位流体的动能。第三项是静水压力,是受重力影响的流体产生的压力。在公式中,G是重力的加速度开yun体育官网入口登录app,H是当前位置和参考位置之间的高度差。这是Bernoulli方程的压力表达。当然,它也可以以头部的形式表达。或以能量的形式。
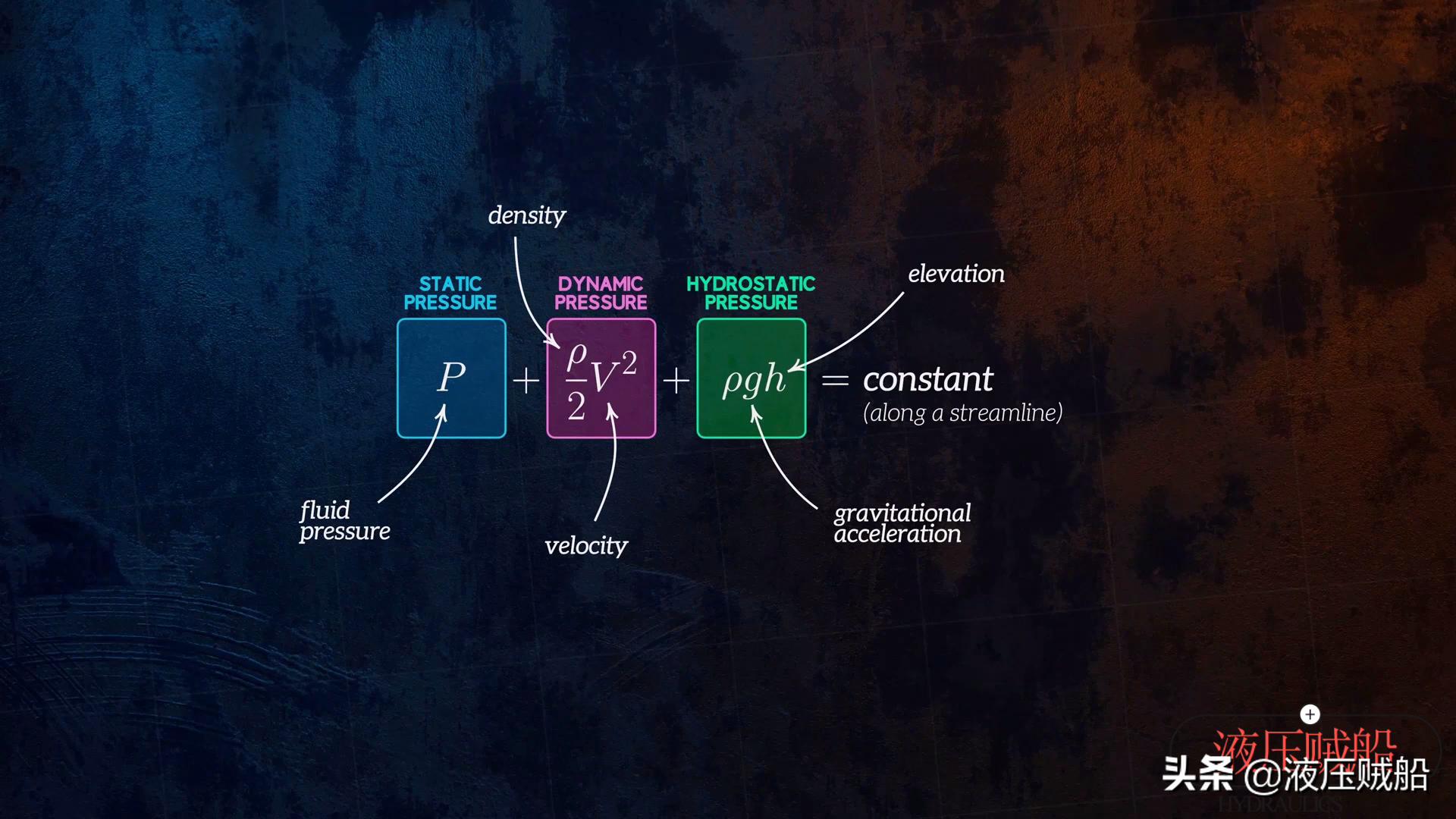
我们还可以将Bernoulli方程视为能量保护定律的表达,这意味着压力能,动能和势能的总和沿流线保持恒定。这是非常有价值的信息,可以帮助我们分析一系列流体流问题。当然,应该强调的是,该方程只能沿流线型方向使用。所谓的流线,我们可以将其定义为稳态流动中流体内部颗粒的流动路径。相反,这是一条曲线,在所有点上都与粒子速度相切。

应用程序1--伯诺利方程在可变直径管道中的应用
在下面,我们应用Bernoulli方程,以查看流体如何通过可变直径管道流动。使用Bernoulli方程,我们可以了解流体压力流经可变管道的压力的变化。它也可以用来比较不同位置的流动条件。为此,我们可以将Bernoulli方程转换为以下形式。
然后,我们在同一流线上获得1和2。由于点1和2之间的高度没有明显的变化,因此我们认为它们大约相等,因此势能项可以被认为是相等的,因此可以彼此抵消。
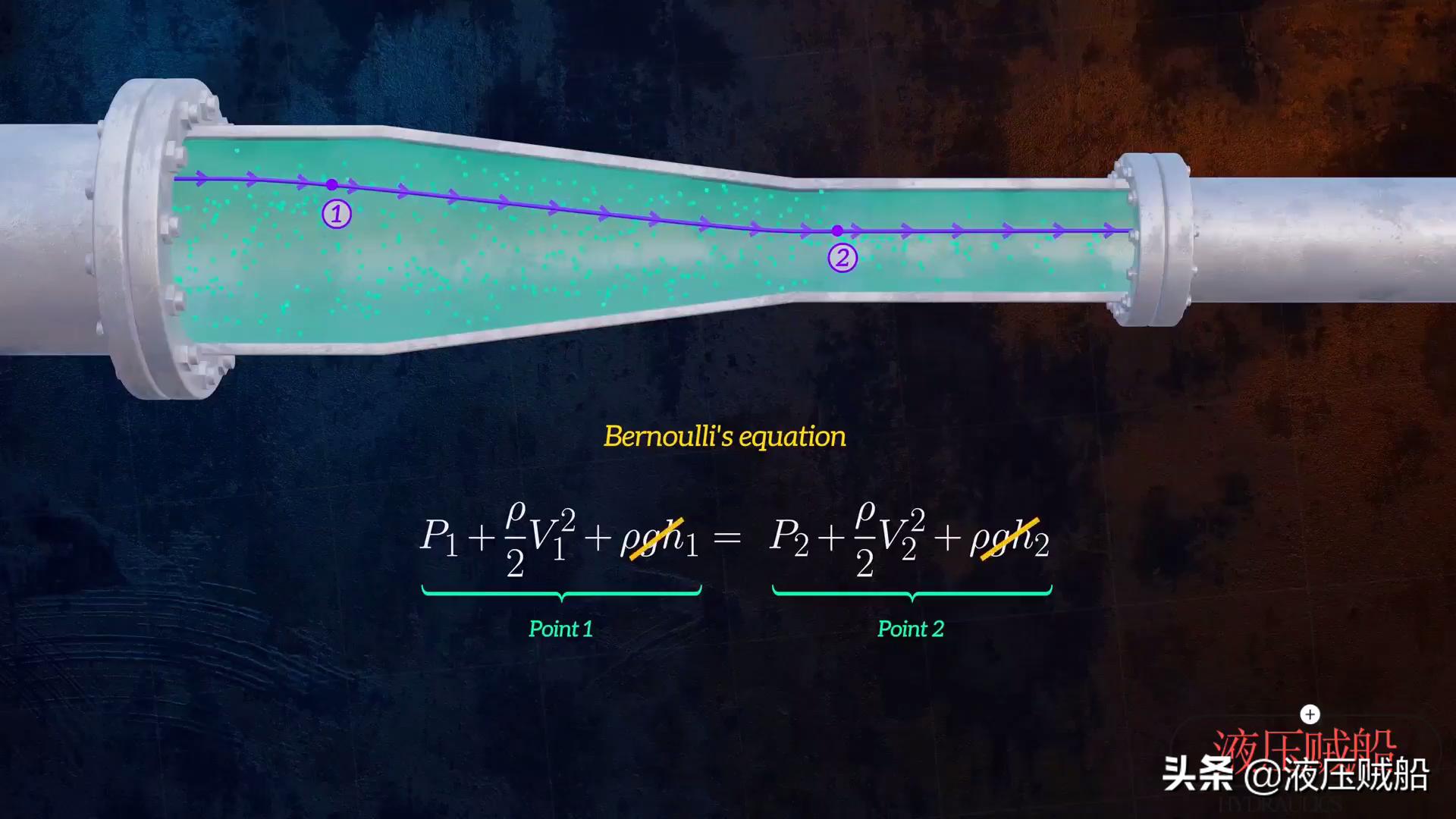
接下来,我们将静态压力项移至相等符号的同一侧,以便我们可以得到压力变化的方程。如果我们假设流体不可压缩,那么点1和2的质量流肯定相等。这是所谓的连续性方程,它是质量保护定律的表达。所谓的质量流量等于流体密度的乘积,管道的横截面区域和流速。因此,转化后,该连续性方程可能成为点2的速度方程。由于横截面A2小于A1,这意味着当流体进入较小的直径管截面时,流速会增加。
接下来,我们将左侧的V2带到右侧的Bernoulli方程式。我们可以看到,流速度从点1到第2点增加开元ky888棋牌官方版,而压力正在降低。

要总结一个句子,对于水平流动,流体速度的增加将不可避免地伴随着流体压力的降低。这是Bernoulli原则最容易理解的表达。尽管每个人都直觉地认为,速度的提高将不可避免地导致压力增加,但事实并非如此。我们还可以从能源损失的角度考虑这一点,即,通过增加流体速度消耗的能量是从流体的静压能量中获得的。
应用2-飞机的升降机是如何发生的?
让我们使用Bernoulli原理来解释为什么飞机的机翼能产生升力?首先,我们知道流动机翼上方流动的流速要比下面的流速快。根据伯努利的原则,将在机翼上方形成一个低压区,并在机翼下方形成亲戚。高压区由于机翼上部和下侧之间的压力差而产生升力。
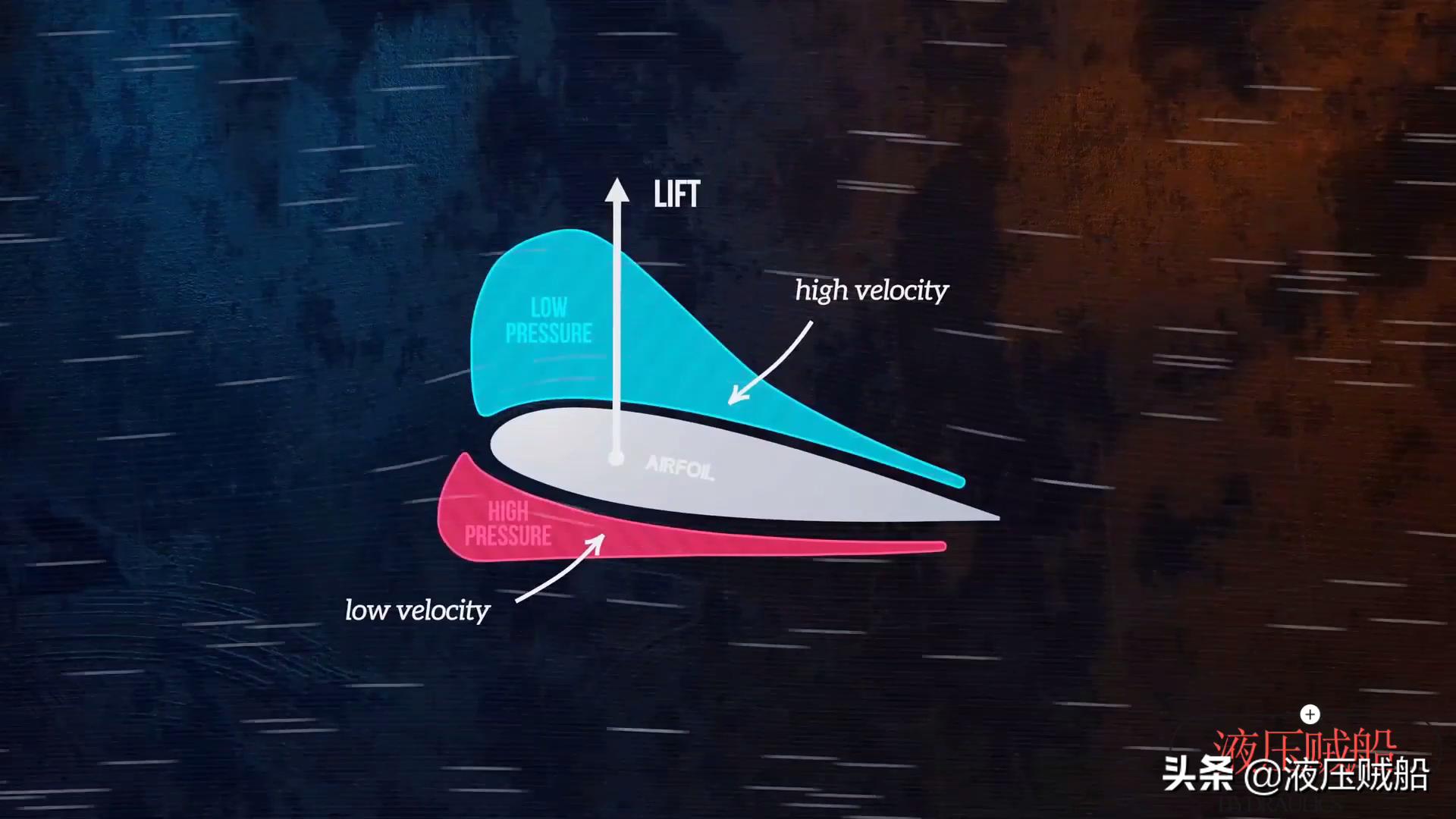
应用3-为什么Bunsen灯可以更充分地燃烧?
Bernoulli原理也可以用来解释Bunsen Lamp的工作原理。打开气门时,气体以更高的速度流入灯管。根据Bernoulli原则,这种高速流将在灯管中产生负面。压力区域会导致外部空气被迫进入灯管,从而使空气和中气更好地混合,并使燃烧更加足够。
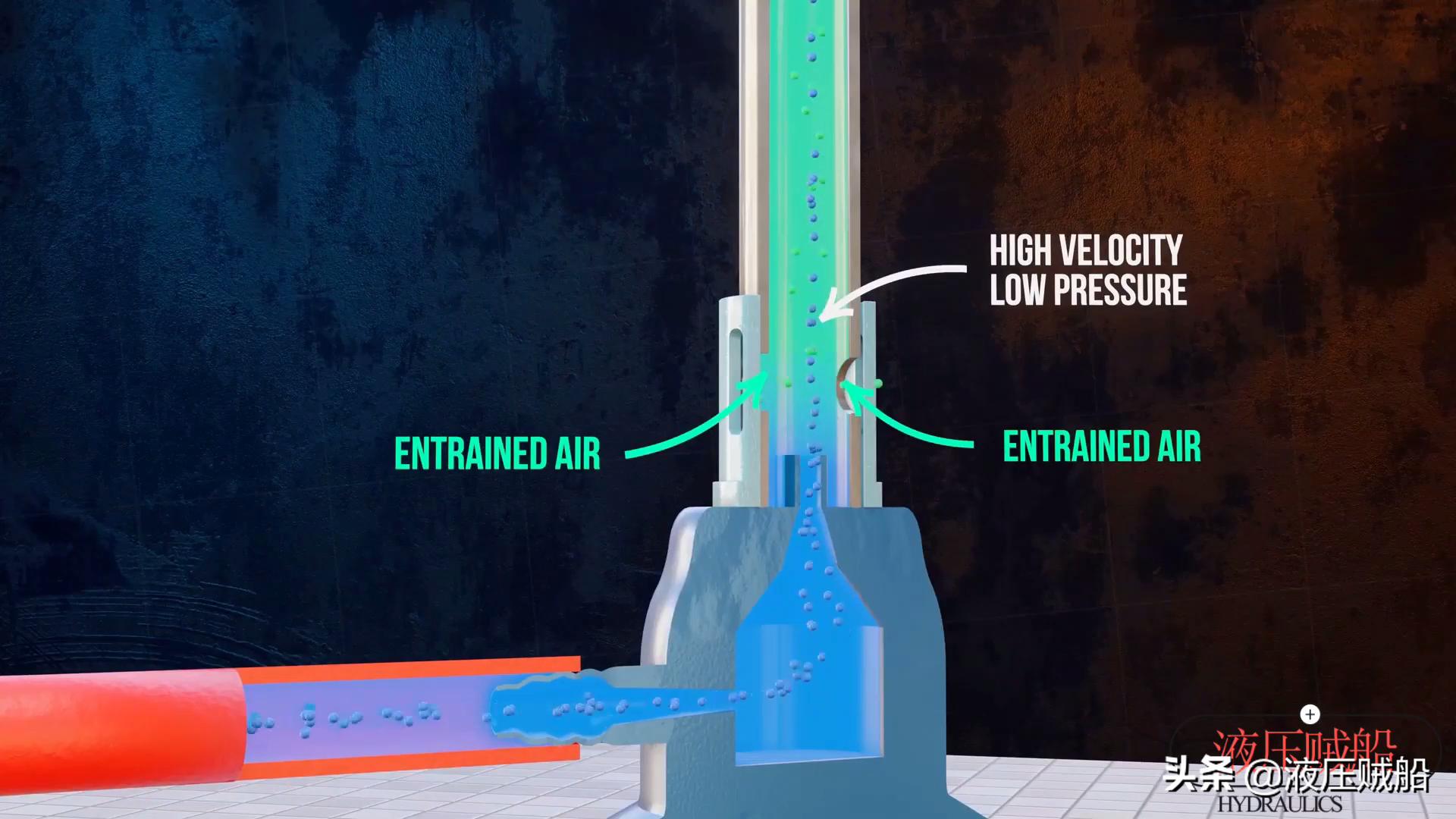
应用4-如何使用皮托管来测量飞机的飞行速度?
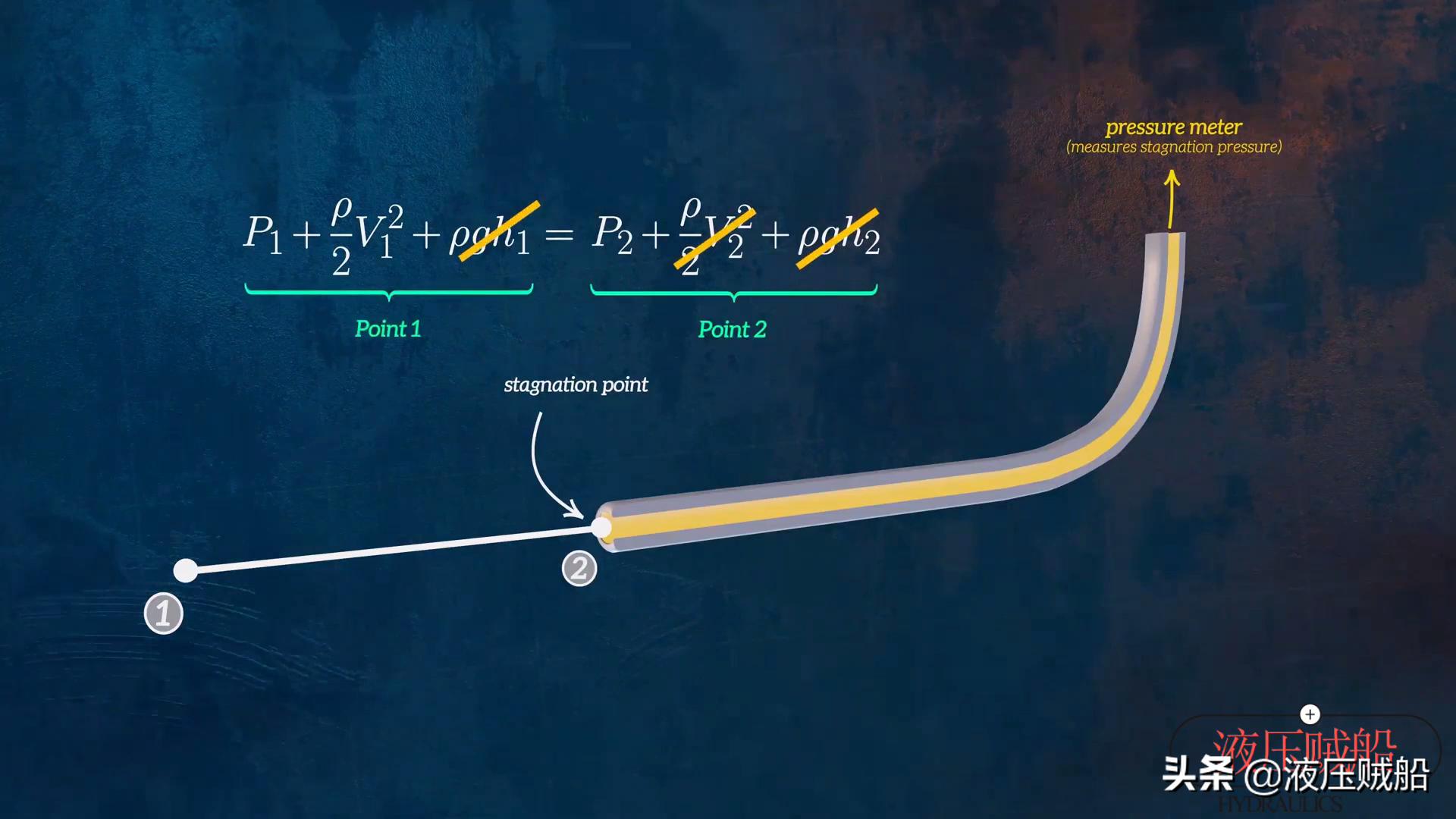
一些流量计还依靠Bernoulli方程来确定流体流体的速度。皮托管是一种通常用于检测飞机飞行速度的设备。让我们在这里简要描述其工作原理。如果将管放入流动的液体中,请在管子的末端安装压力。仪表,压力表将检测到管末端的压力。管道入口处的流体速度为零,我们称之为停滞点开yunapp体育官网入口下载手机版,此时测量的压力称为停滞压力。我们可以在上游点1和停滞点2之间应用Bernoulli方程。由于两个点的势能大致相等,并且停滞点2处的速度V2等于0,因此,点2的停滞压力等于要点1位于位置的静压和动态压力之和。也就是说,点1处的所有动能基本上都会在停滞点2转换为压力能。目前,如果我们将密封端的外管放置在管道的外部下游,将一个小孔打开,外管测量流体的静压,而不是停滞压力,我们知道这两个我们可以通过压力轻松确定流速。

应用程序5 - - 文丘里流量计如何工作?
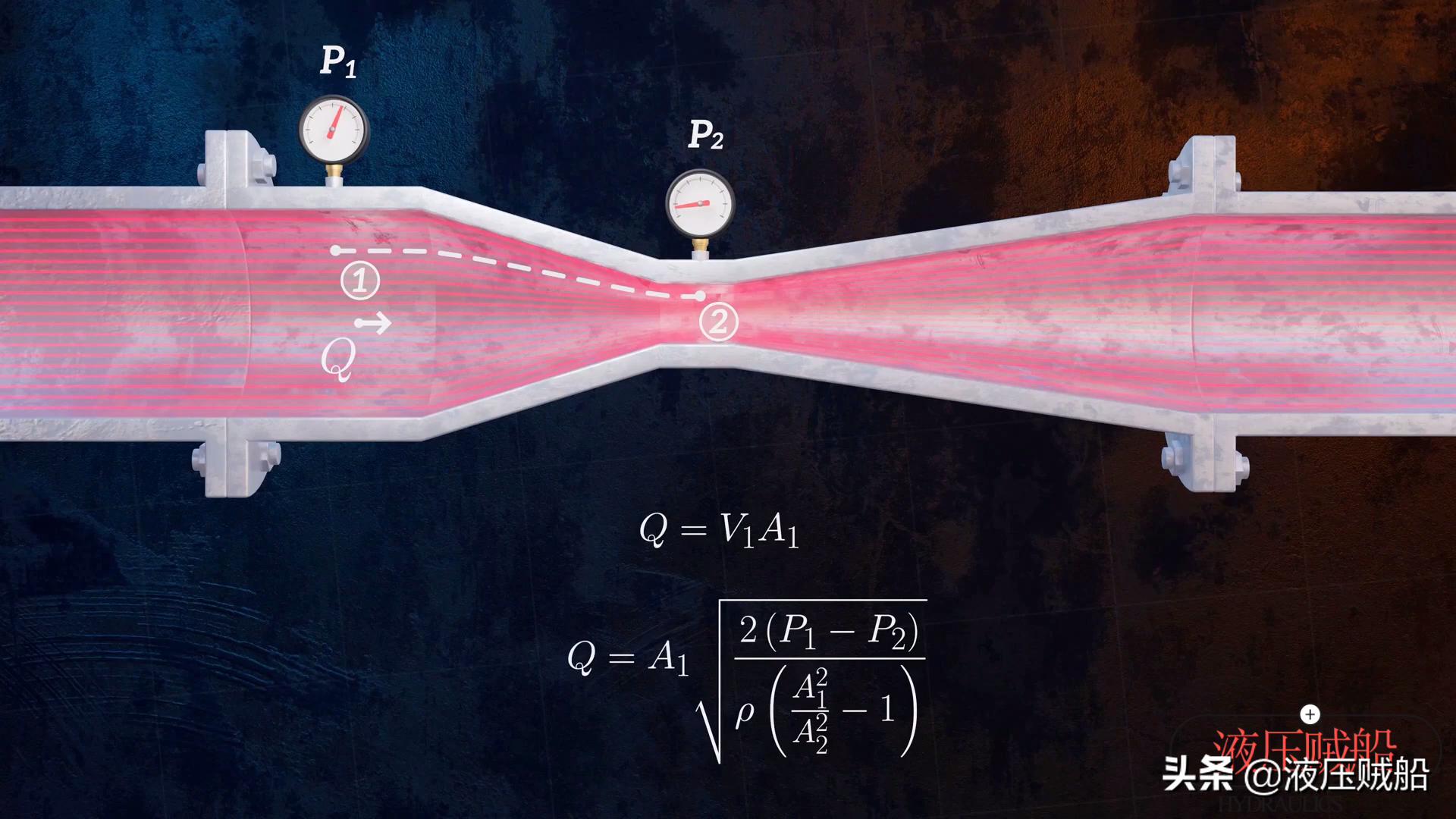
使用Bernoulli方程式制造的另一个流量测量设备是Venturi流量计,该仪表用于确定管道中介质的流速。它主要测量流过管道收缩部分的流体的压降。在职的。假设我们要确定流速Q,即流速乘以点1处的管道横截面区域,我们可以转换压降方程以获取流速的计算公式。我要接下来要做的是确定文丘里流量计的大小,流体密度,压力P1和P2,以便可以计算流速。 Venturi流量计内部没有移动部件,并且是一种简单可靠的管道流动检测设备。其扩散部分的长度明显长于收敛部分的长度,这可以显着降低能量损失。
应用6-如何计算从容器中流出的液体速度?
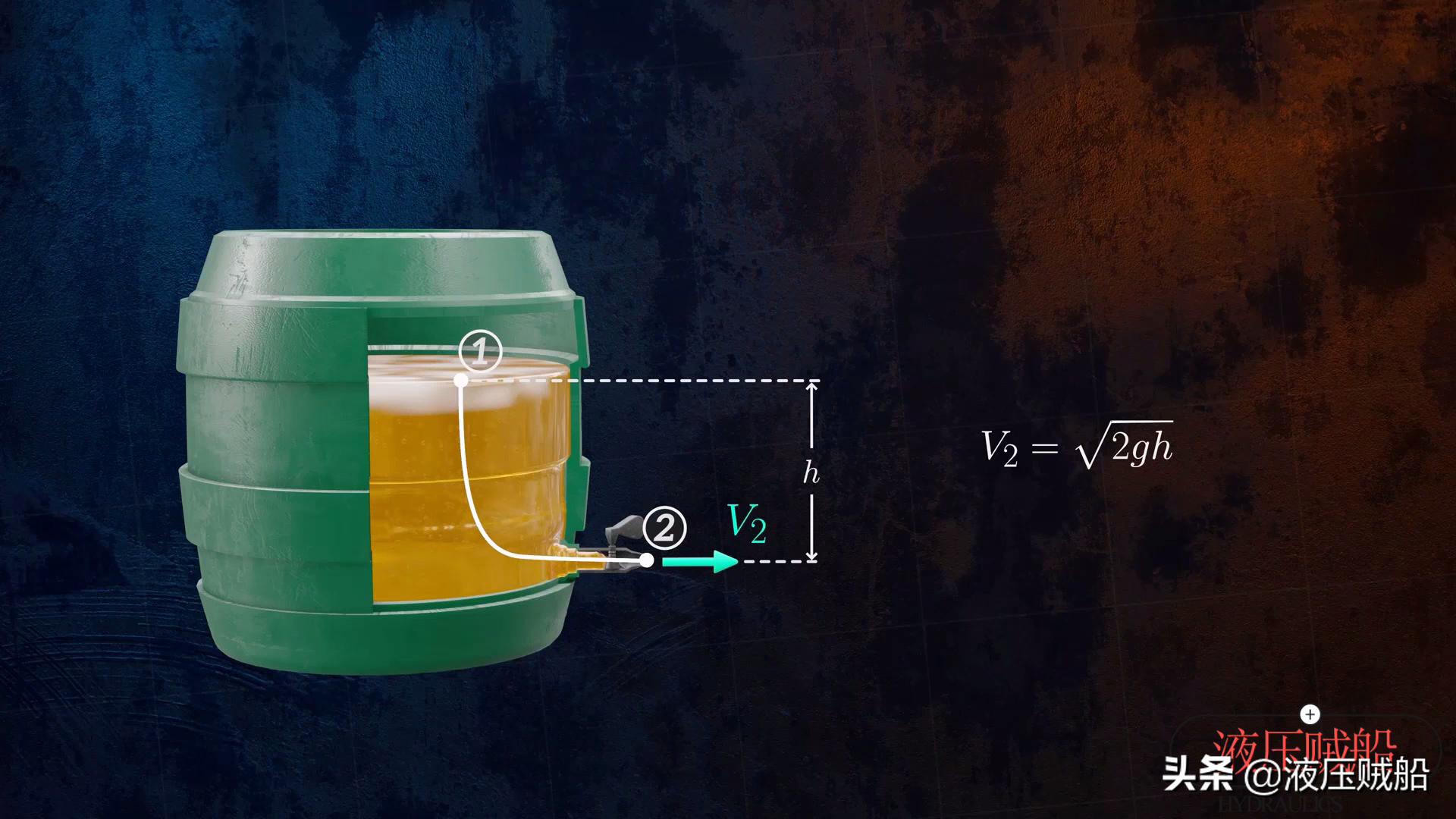
让我们看一下如何使用Bernoulli方程计算从容器中流出的液体的速度?假设我们有一个啤酒桶,现在想计算枪管的排空速度,我们需要做的第一件事是打开枪管底部的水龙头,然后在某个流线上定义两个点两个分。应用Bernoulli方程。
该枪管的顶部有一个呼吸端口,这意味着其顶部连接到大气,龙头的出口点2也连接到大气,因此点1和2处的静压是大气压力可以彼此忘记。此外,我们假设枪管足够大,可以认为点1的流速约为0。现在,让我们更改Bernoulli方程,并将啤酒液位和水龙头之间的高度差定义为H,这样我们就可以获得啤酒流量的表达V2。
使用Bernoulli方程来限制条件
好的,以上是我们生活中的一些例子,您也可以尝试应用Bernoulli方程来解决一些实际问题。但是,如果您想正确使用它,那么了解其推导方法及其应用程序限制非常重要。我们对派生过程没有太多解释,但是我们必须了解我们在派生过程中人为地做出的假设?这些假设将限制Bernoulli方程的应用范围。
第一个假设是流体的流量是层流和稳态,这意味着流动不会随时间变化。
第二个假设是流体不是粘性的,即,实际流体的粘度产生的剪切应力被忽略。该假设是必不可少的,因为流体的粘度会导致流体内的能量损失,从而导致能量沿流量线保持。结论不再适用的结论。
第三个假设是流体不可压缩,这意味着它通常仅适用于液体,并且可能不适用于高速流动气体。
总而言之,如果您想应用Bernoulli方程,则必须同时满足以上三个假设。
当然,有一些修订版的Bernoulli方程式,虽然更复杂,但可以应用于非稳定和可压缩流体的流动。
好的,这就是今天的内容,下次见。




