神奇的斐波那契数列

如果我们将一些数字提升为行，则形成配额。这些数字可能是常规的，可能没有规则的，也许是有限的数字组成，或者可能是无限数量的数字。

例如，1、2、3、4、5 ....它构成了许多列。

另一个例子是1、2、4、8、16 ...也构成一个数字。后者的比例和上一项不变，称为相等的数字列。

在本质上，有数百年的列表已经进行了广泛讨论，这就是“兔子编号列”，也称为斐波那契数列。接下来，让我们一起学习！

阿拉伯数字

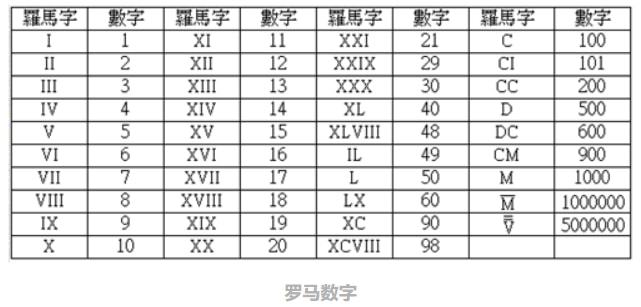
在十二世纪之前的欧洲，由于宗教原因，科学和数学的发展非常慢。欧洲人也习惯于使用罗马数字。罗马有7个数字，即：ⅰ（1），ⅴ（5），ⅹ（10），hip（50），ⅽ（100），ⅾ（500）和ⅿ（1000）。

它的计数规则也相对复杂。例如：两个数字并排排。如果右侧的数字小于左侧的数字，则表示添加了两个数字；如果右侧的数字大于左侧的数字，则意味着两个数字希望减少要减少的两个数字。本质也有许多复杂的规则，这些规则非常不便。

在十二世纪，欧洲数学有恢复的迹象。这是因为与阿拉伯国家和十字军东征的贸易一直与阿拉伯世界接触。目前，阿拉伯正在使用诸如1234567890之类的符号来表示数字，这非常方便。由于这个数字是从阿拉伯国家汲取的，因此称为阿拉伯数字。

但是实际上，在公元前三世纪，印第安人已经使用了类似的方法来表示数字。阿拉伯数字是由印第安人发明的。在公元7世纪，这一数字被介绍给阿拉伯，后来又通过欧洲传播到了世界。

fibonacci编号列

Fibonati（也称为Pizza Leno）是一位意大利数学家。他年轻的时候，他与北非的父亲一起学习了阿拉伯语。

1200年，斐波那里回到了意大利。在1202年，它被写成“计算技能”，这对欧洲的数学社区产生了巨大影响。

在这本书中，斐波那蒂提出了一个有趣的问题：

如果有一对新出生的小兔子，那么一个月就可以成长为一只大兔子。从第三个月开始，大兔子每月都会有一对小兔子。新生儿兔子将长大一个月，然后再花一个月开始兔子……如果每对兔子都会经历这样的出生，成熟和生育过程，并且永远不要死开元棋官方正版下载，那么总数是多少每月兔子，每月兔子的总数是多少。羊毛布？

我们不妨先研究这个问题。

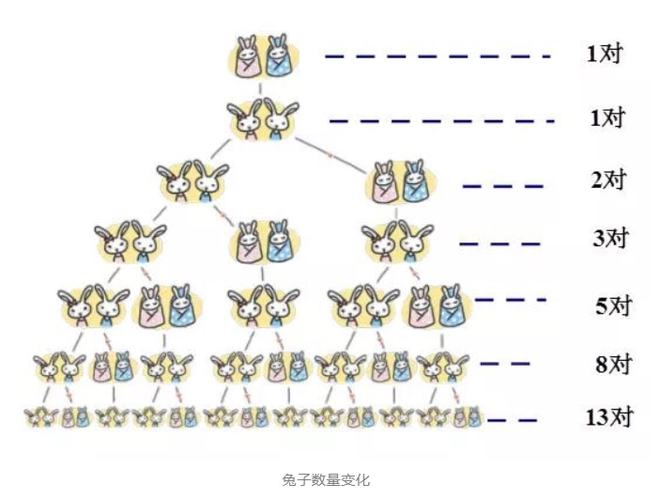
在第一个月只有1对兔子。第二个月只有1对大兔子。在第三个月中，大兔子生下了一对兔子，一对兔子。在第四个月，大兔子继续生了一对婴儿，小兔子变成了大兔子。两对大3对兔子...

结果，每个月的大兔子，小兔子和总共兔子的数量构成了三个数字。

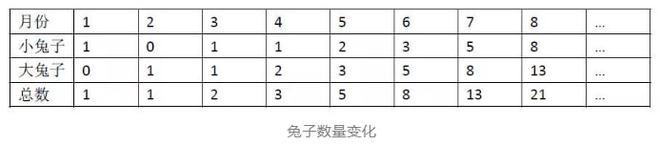
我们发现它会发现是兔子的数量，大兔子的数量还是兔子的总数。除前几个数字外，其后是1、1、2、3、5、8、13 ...此列称为兔子号列。因为它是斐波那契最初提出的，所以也称为斐波那契。

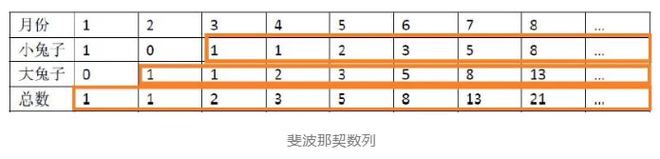
兔子数系列的最大特征是前两个项目的总和等于后者，例如1+1 = 2，1+2 = 3，2+3 = 5，3+5 = 8，5 +8 = 13 ...

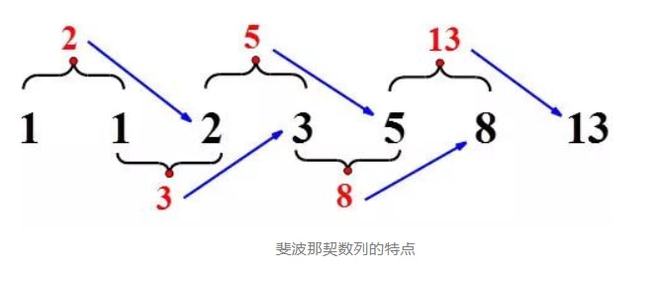
我们使用A表示系列的NN项目，然后斐波那契系列的定律“第一个和第二个项目是1，前两个项目的总和等于后一个项目”：

这种数学表达称为复发类型。从复发类型的前一个或几个项目中，您可以计算所有后续数字。

兔子数的用途是什么？

也许许多读者认为斐波那契系列只是数学海洋​​中的一滴水。但是，从本专栏的当天开始，已经有800年了。人们继续增加对它的兴趣，并且在许多地区都发现了阴影。

关于数学中的“方法”有很多问题，答案通常是斐波那契号。

例如，这样一个问题：我们必须走上N级步骤的楼梯，我们只能迈出一个小步骤（1平方）或每次迈出一个大步（2个网格）。那么在楼梯上行走的方式有多少种？

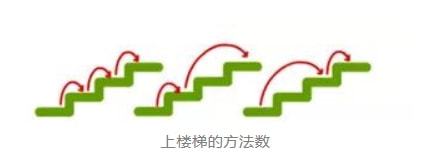
我们从最简单的情况开始分析：

如果只有一个步骤级别，您只能加强一步，显然只有一种方式。

如果有两个步骤，则可以越过一个步骤开元ky888棋牌官方版，也可以分为两个步骤，因此有两种方法。

如果有三个步骤，则有三种方法需要如图所示：分为三个小步骤，一个小步骤，一个大步和一个小步骤。

如果还有更多步骤怎么办？这需要叙述。因为一个步骤有两个步骤，所以有两个方案可以达到NI级别：有两个解决方案：

1。转到N-1步骤，然后迈出一小步到顶部；

2。转到N-2步骤，然后迈出一大步。

我们使用AN-1和AN-2指示进入N-1和N-2步骤的方法数量，因此达到NI级别的方法数为：

显然，这是斐波那契号的递归公式，因此步骤的解决方案恰好是斐波那契数。

生活中最典型的斐波那契数字应用是在植物中。

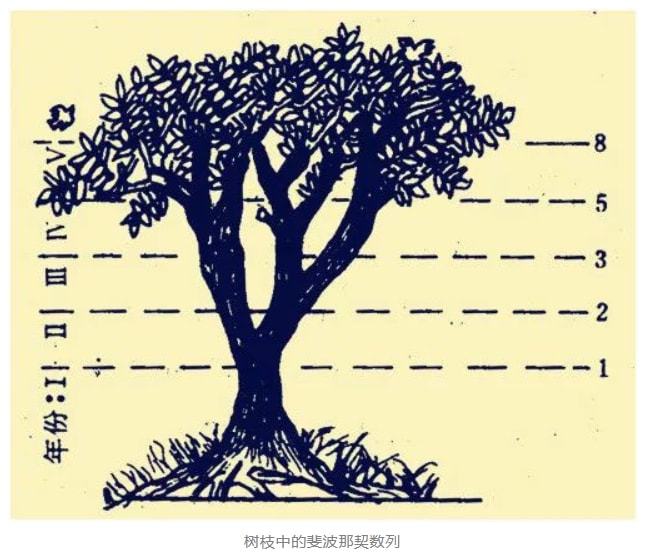
在大树的成长过程中开元ky888棋牌官网版，分支机构是总统。如果我们从底部到顶部都有许多分支，我们会发现它是1、2、3、5、8、13 ...等等。 Bonaci计数。一些科学家对这种现象有相同的解释，即它们与兔子的萌芽后代相同：每次经过一段时间后，新的芽都会发芽，而新的芽将成长为成熟的分支。新芽将每隔一次发芽。

另一个神奇的例子是诸如向日葵之类的植物。

如果仔细观察，我们会发现向日葵磁盘中的种子形成了两组螺旋线，一组是顺时针方向，另一组是逆时针。这两组螺旋线的数量正好是两个相邻的纤维，小的向日葵为34和55，大的向日葵为144和233。

一些科学家认为，这种布置可以使种子的种子成为最密集，也是最有利于植物繁殖的种子。

在过去的800年中，人们在各个领域发现了斐波那契系列。尤其是自19世纪以来，人们发现斐波那契数在计算机，物理，化学和其他领域的领域中的应用。这个古老的数字使新的青年恢复活力。 1963年，建立了斐波那契协会并发布了“斐波那契季节”，以发布与斐波内利配额有关的研究结果。