第A7篇 贝叶斯定理（统计在生活中的应用）

贝叶斯定理已在统计基础的第七章中引入了“贝叶斯定理 - 概率校正方法”。最近，我再次遇到了这个概念，并认为它可以反映统计在生活中的应用，因此我分享了它并与所有人仔细咀嚼。

背景简介

贝叶斯（托马斯·贝叶斯（Thomas Bayes），1701- 1761年）是英国人，他的主要职业是牧师，他的爱好是数学。为了证明上帝的存在开元棋官方正版下载，他发明了概率统计原则。尽管他的美丽愿望直到他去世，但他为统计的发展做出了巨大贡献。

维基百科对贝叶斯定理的起源的描述：所谓的贝叶斯方法源自他写的一篇文章，目的是解决他一生中的“反向”问题，该文章是由一位朋友去世后出版的。在贝叶斯（Bayes）撰写本文之前，人们能够计算“正概率”，例如“假设袋子里有n个白球和M黑球，您可以伸手去拿并触摸它，以及找到黑球的可能性是什么。”另一个自然的问题是：“如果我们不知道提前袋中的黑白球的比例，而是闭着眼睛拿出一个（或几个）球，观察到这些被带球的颜色的颜色，那么我们可以猜测书包里的黑白球的比例。”这个问题是所谓的反向一般问题。

定理评论

贝叶斯定理的一个流行解释：在使用概率推断事件之前，我们经常掌握了此事件的可能性。此概率可能是主观的概率或相对概率（查看概念，请回复5）。此初始概率可以称为先验概率。如果在随后的研究中，通过采样调查样本和其他信息来源获得了有关事件的信息，我们可以基于此新信息纠正先验概率，以将先前的概率更改为后验概率。该校正概率的定理称为贝叶斯定理。

贝叶斯定理公式（衍生过程回复7）：

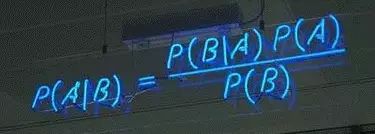
向每个人解释了一个详细的例子：假设三个工厂A，B和C的相同部分的市场份额分别为10％，25％和65％。众所周知，A，B和C产生的零件的不合格率分别为30％，20％和10％。现在，从市场上的一批零件中随机选择了一块。在被发现不合格之后，a，b和c产生零件的概率是多少？

解决方案：在提取零件之前，我们知道来自三个工厂A，B和C的产品分别占10％，25％和65％。这些是先前的概率。我们在市场上提取的产品现在是不合格的产品。这是一个新信息。我们可以使用此信息来获得后验概率。分析过程如下表：

A，B，C和三个不合格部分的生产案例

工厂

事先概率

有条件的概率

关节概率

后概率

0.1

0.25

0.65

0.3

0.2

0.1

0.1*0.3 = 0.03

0.25*0.2 = 0.05

0.65*0.1 = 0.065

0.03/0.145 = 0.207

0.05/0.145 = 0.345

0.065/0.145 = 0.448

1.00

0.145

1.000

我们可以看到，先前概率和后验概率之间存在变化，这是根据条件概率校正先前的概率。

生活应用

以下例子是医学中常见的问题，与现实生活密切相关。

有一种疾病，发病率为1,000。医院的实验室技术可以诊断出这种疾病，但是误诊率为5％（也就是说，尽管有5％的人没有生病，但测试结果表现为阳性（即误报）。现在，假设一个人的测试结果证明是病了开元ky888棋牌官网版，基于此测试结果，这个人的可能性是什么？

该问题的分析过程如下：

事先概率：

P（疾病）= 0.001

P（正常）= 0.999

条件概率（新信息）：

p（准确率）= 1.00;精度率（检测到100％的患者）。

P（误诊率）= 0.05;误诊率（5％的正常人被误诊）。

基于上述数据，我们可以推断，如果一个人的测试是正面的开yun体育app入口登录，那么该人实际生病的可能性（后验概率）是：

p（疾病|阳性）= p（疾病）×p（准确性）/[（p（疾病）×p（准确性） + p（正常）×p（误诊率）]

= 0.001×1.00/（0.001×1.00+0.999×0.05）

= 0.0198

= 2％

结果使您感到惊讶。如果没有其他症状会增加疾病的可能性，则单独的测试结果显示阳性，那么疾病的实际概率小于2％。因此，应针对年度常规体格检查引起的问题进行重新检查。