图像处理中的应用
1个信号处理中的卷积
无论是信号处理,图像处理还是其他一些字段,我们经常在某些相互关联的数据处理中使用卷积。可以说卷积是算法中非常重要的概念。这个概念起源于信号处理。
假设对于线性系统开yun体育官网入口登录app,在单位脉冲δ(t)的响应中,其输出为H(t)。然后,在Aδ(t)的响应中,输出为AH(t)。所有信号都可以通过将系数的总和乘以δ(t)来表示。现在
。也就是说,任何时候
输出是
卷积的来源及其物理含义和在线介绍了许多介绍。我不会再谈论它了。卷积的物理含义主要反映在以下四个方面:
信号响应的计算和多项式关系滤波器在图像处理中的应用2 MATLAB中的卷积函数
MATLAB提供了两个常用的卷积功能,即Cons和Conv2。它们分别用于计算一维卷积和二维卷积。这两个功能都是离散数据的卷积,因此我们将分别讨论这两个卷积。
2.1一维卷卷曲函数
通过在先前的信号处理中引入卷积,我们将其离散化以获得以下离散的一维卷积表达:
u和v是卷积信号,y是输出信号。由于MATLAB中矩阵访问的角度标记从1开始,对于MATLAB中的输入矩阵U,V的卷积输出y为:
卷积和多项式
实际上,我们可以将两个多项式之间的乘法视为其系数矩阵之间的卷积。例如
之间的产物可以被视为u = [1 0 1]和v = [2 7]之间的卷积。目前,卷积后的结果序列长度为尺寸(u)+大小(v)-1。相应的MATLAB代码如下:
clear
clc
u = [1 0 1];
v = [2 7];
w = conv(u,v)执行结果为W = [2 7 2 7],表明由U和V获得的相应多项式为:
由于卷积满足了换向法律,因此U和V和V和U的卷积结果是一致的,也就是说,Cons(U,V)和Conv(V,U)的结果是相同的。
卷积和过滤器
另一方面,我们还可以将卷积视为过滤过程(FIR),u作为过滤信号,而V作为过滤器。目前,过滤后获得的结果序列长度与U相同。在v。中有一个过滤中心点,在卷积乘法和添加过程中,与“时间”相对应的中心点的滤波器值始终乘以相应的卷积结果时间的值。中心点的位置通过翻译过滤器序列更改。下图将直观地解释这一概念。对于信号处理,由于只能知道过去矩的信号,因此应在V(IE V [0]的第一个元素上选择中心点)。对于整个序列已知的信号(例如图像处理),通常在尺寸(v)/2+1处选择中心点的位置(如果不能对其进行分配,则将其选为此值的左侧或右侧)。特殊如果所选的滤波器值相等,而总和为1,则是平均过滤器。下面是平均过滤器的滤波器图,中心点为v [0],大小(v)= 3:
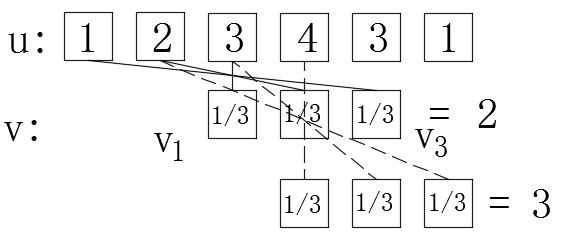
在上图中,为了促进卷积过滤器的物理意义的观察,我们直接找到了W [2]和W [3]。图中的连接线表明需要乘以两个连接的数字。可以看出,目前V等于滤波因子过滤U的相应值。我们看到对V的单位脉冲响应,因此它也称为FIR(有限脉冲响应)滤波器。
对于图像处理或知道整个信号序列值时,过滤器的中心点通常是在v的中心(或左右)中选择的。如果在MATLAB的呼叫过程中添加了相同的参数,则意味着卷积被视为过滤器,并且滤波器的中心点是滤波器的中心点(V)/2+1+1或round(size size size(v)/2)(v is osge n osd osge nesect)。以下是MATLAB中计算代码和计算过程的示意图,其中卷积被视为过滤器,并且过滤器的中心点位于中间:
clear
clc
u = [1,2,3,4,3,1];
v = [1/3 1/3 1/3];
w = conv(u,v,'same')执行结果:
w =
1.0000 2.0000 3.0000 3.3333 2.6667 1.3333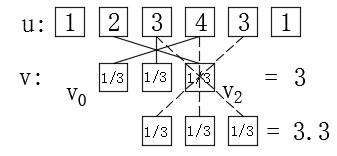
我们发现,将卷积视为过滤器(过滤器操作员)后,我们始终需要在乘法和加法过程中跨V。这也是为什么图像处理中各种操作员和相应的卷积内核总是被180°逆转的原因。这个问题有两种解决方案。一种是在过滤过程中更改卷积公式,并将减法更改为加法,以将过滤器卷积公式定义为:
。第二个解决方案是接受相反的事实,并在绘制相关图时手动将其转动180°。我们还可以扭转以上两张图片,并更愉快地看到它们:
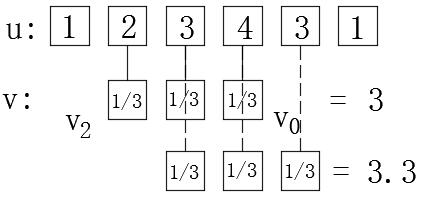
在信号过滤中,通常选择过滤器的中心点在最左边,而在图像处理中,通常选择过滤器的中心在中心位置。在其他位置使用较少。实际上,可以通过转移和截断上一节的一般卷积结果来获得任何中心位置的卷积结果。
除了相同的参数外,MATLAB还提供了有效的参数来计算有效的过滤点号。所谓的有效数量点是中心点位于滤波器中心的数据点,可以使用滤波器数据计算。例如,上面的W [0]不是有效的数据点。从图像处理的角度来看,操作员没有足够的数据来计算边界,然后丢弃这些点。 w = max的计算长度(长度(u)-length(v)+1,0)。以下是MATLAB示例,您可以体验它:
clear
clc
u = [1,2,3,4,3,1];
v = [1/3 1/3 1/3];
w = conv(u,v,'valid')执行结果如下:
w =
2.0000 3.0000 3.3333 2.66672.2二维卷积Conv2功能
像以前的一维卷积一样,我们可以将卷积的概念推广到二维卷积。二维卷积的最常用位置是图像过滤。在这里,我们称使用用于卷积内核的过滤器,以及一些常用的卷积内核,我们也称其为某个操作员。例如,SOBEL操作员通常用于边缘检测。实际上,由于卷积的概念来自数字信号处理,因此操作员和卷积内核只是对中心点的对称性(我们之前已经解释过)。但是,没有引起混乱,我默认它们是一样的,不再区分它们。
首先,让我们看一下二维卷积的定义。您可以使用Doc Conv2参考MATLAB中的描述文档,但应注意的是,MATLAB中的角度标记从1而不是0开始,并且公式将有些不一致。
两个二维矩阵A和B的卷积结果C可以通过以下公式表示:
对于C = Conv2(A,B),如果[MA,Na] = size(A),[MB,NB] = size(C)开元ky888棋牌官方版,[MC,NC] = size(C)。然后mc = max([MA+MB-1],MA,MB),NC = Max(Na+NB-1,Na,NB)。
对于二维卷积结果中的一个点C(M,N),它实际上是在A(M,N)周围和B中的所有点乘以相应的点并将其求和(假设B矩阵的尺寸小于A)。在图像处理中,A(m,n)周围的点指的是(m,n)周围的点为中心。特定的含义可以在百度的“二维卷积”中找到,通常有图片,所以我不会在这里绘制图片。我在线拍摄了一张随机的照片,这大致意味着:
当Matlab调用二维卷积时,它还提供了三个可选参数:
full: 计算两个二维矩阵的常规卷积(默认参数),和一维卷积一样
same: 和一维卷积一样
valid: 和一维卷积一样当参数在上述三个参数之间已满时,表示的含义与信号处理中卷积的含义相同。当参数相同时,相应的卷积公式为:
上面的公式实际上是在原始的卷积公式中,该公式将卷积内核转移到右侧和向下,并将整个单元向下转移。也就是说,让卷积内核的中心对应于计算的卷积点。以下是在完整参数和相同参数下卷积的物理意义的比较,以C(0,0)为例。
对应于完整参数的公式:
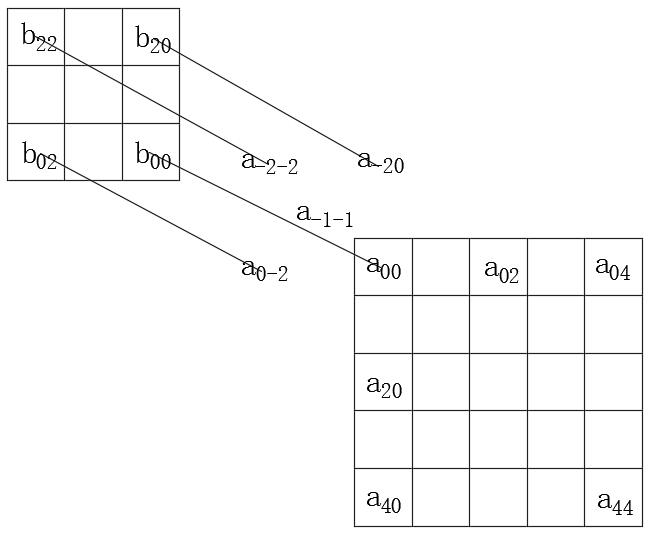
相同参数的相应公式:
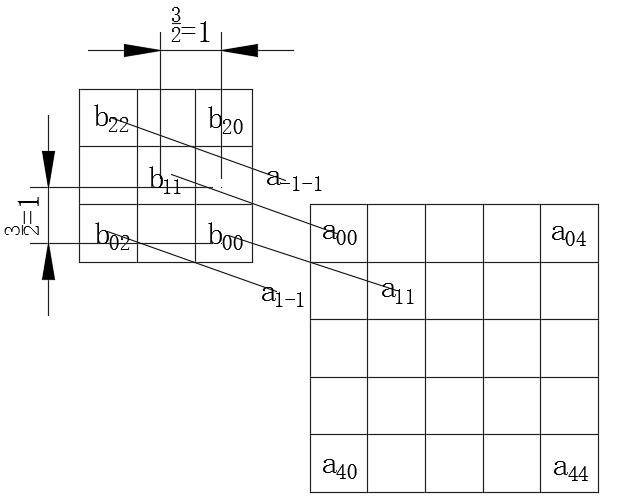
可以看出,当将完整参数计算并计算为查找C(0,0)时,从图像中首先将B矩阵旋转180°(请注意,B矩阵的左上角为(2,2)为(2,2),右下角为(0,0,0),然后是A(0,0)和B(0,0,0,0),然后对(b(0,0,0,0))对准,并将其对准并均为乘数(均为乘数)。在这里,可能涉及矩阵边界之外的点。
一般计算过程并未根据相同的参数变化太大。只是我们不对准A(0,0)和b(0,0),而是对齐矩阵A(0,0)和B(行时圆形)的中心点B(MB/2,NB/2)。在这里开yunapp体育官网入口下载手机版,它可能涉及矩阵边界之外的点。
由于我们通常不知道边界之外的点状况,因此MATLAB提供了一个有效的参数。当在此参数下计算卷积时,如果使用矩阵边界以外的一个点来计算卷积点C(i,j),则将删除卷积结果。相应的公式为:
该公式的想法与在相同参数下的公式的概念相同。只是在此处计算C(0,0)时,A(0,0)和B(2,2)对齐。由于A(0,0)和B(2,2)在计算时都是矩阵的右上角元素,因此计算C(0,0)时,矩阵边界之外的点将不使用。接下来计算时,只需确保卷积内核B不会在A矩阵外移动即可。
除了上面的一维卷积外,MATLAB还提供了另一个呼叫表格,即C = Conv2(H1,H2,A)。它首先要努力A和H1的每一列,然后将结果的每一行和H2卷入。如果N1 =长度(H1),N2 =长度(H2),则MC = Max([MA+N1-1,MA,N1]),NC = Max([Na+N2-1],Na,Na,N2)。一般而言,我们使用此通话表格少。
2.3边界扩展
MATLAB的卷积计算过程使用标准计算公式来查找信号处理中的系统响应(图像处理等实际上在标准卷积结果中截获)。目前,图像处理中“边界”之外的点被认为是0。但是,在计算机图形学中,有时我们认为这是一个合理的假设。例如,此图像以大图像拍摄。我们认为,边界点以外的点大约等于边界上的点。否则此图片是周期性的周期图。我们在此期间拍摄图像。目前,认为边界之外的点等于另一个边界上的点更为合适。
此外,当一部分卷积内核在边界外运行时,我们要放弃这些观点。目前,我们可以使用有效的参数将其丢弃。
3。卷积的C ++实施
为了使我们的代码在计算系统响应,多项式乘法,滤波器设计和图像处理中更一般性,除了实施上面MATLAB中提供的卷积实现之外,我们还需要添加MATLABCONV2函数中不可用的边界处理条件选择。
可选边界条件包括:边界外部的点为0(默认值),边界和边界值之外的点相等,边界之外的点以及另一个边界上的点以及另一个边界上的点形成周期信号。
在此处实现C ++卷积算法时,使用C ++矩阵计算库EIGEN。
应当指出的是,当此处实施卷积时,将Cons和Conv2合并。实际上,在MATLAB中的大多数情况下,可以使用CONC2代替CONC,因此Cons和Conv2在C ++实施中不再区分。但是,应注意的是,使用Conv计算行向量的卷积,而列向量是向量,而使用Conv2是矩阵。在这方面,Cons和Conv2之间存在差异。因此,如果您确保在使用时正在寻找一维卷积,请确保两个向量都是行向量或列向量。这是MATLAB的示例:
clear
clc
a = rand(1,3);
b = rand(3,1);
c = conv(a,b)
d = conv2(a,b)
e = conv2(a,b')
执行结果:
c =
0.1409
0.4958
0.2941
0.1608
0.0380
d =
0.1409 0.0357 0.0384
0.4601 0.1165 0.1255
0.1391 0.0352 0.0380
e =
0.1409 0.4958 0.2941 0.1608 0.03803.1简单地实施C ++中的卷积
通过上述分析,我们首先编写一个更简单的卷积功能来验证该功能。然后将此功能封装到类中。简单的C ++卷积代码如下:
#include
using namespace std;
enum BoundaryCondition
{
zero
,bound
,period
};
enum Method
{
full
,same
,valid
};
//参数设置
const int A_Row = 4;
const int A_Col = 5;
const int B_Row = 2;
const int B_Col = 3;
BoundaryCondition Bc = zero;
Method method = full;
float A[A_Row][A_Col] = {{1,2,3,4,5},
{2,3,4,5,6},
{3,4,5,6,7},
{4,5,6,7,8}};
float B[B_Row][B_Col] = {{1,2,1},
{2,3,2}};
float** C = 0;
int cR;
int cC;
template
T GetA_Ele(int row,int col);
template
void conv(const T a[][A_Col],const T b[][B_Col],T**& c);
int main()
{
conv(A,B,C);
for(int i = 0;i < cR;i++)
{
for(int j = 0;j < cC;j++)
cout<
void conv(const T a[][A_Col],const T b[][B_Col],T**& c)
{
int offsetR = 0;
int offsetC = 0;
switch(method)
{
case full:
cR = A_Row + B_Row - 1;
cC = A_Col + B_Col - 1;
break;
case same:
cR = A_Row;
cC = A_Col;
offsetR = B_Row/2;
offsetC = B_Col/2;
break;
case valid:
cR = A_Row - B_Row + 1;
cC = A_Col - B_Col + 1;
if((cR < 1)|(cC < 1))
return;
offsetR = B_Row - 1;
offsetC = B_Col - 1;
break;
default:
return;
}
c = new T*[cR]; //给二维数组分配空间
for(int i = 0;i < cR;i++)
c[i] = new T[cC];
for(int i = 0;i < cR;i++)
{
for(int j = 0;j < cC;j++)
{
c[i][j] = 0;
for(int k1 = 0;k1 < B_Row;k1++)
{
for(int k2 = 0;k2 < B_Col;k2++)
c[i][j] += b[k1][k2]*GetA_Ele(i - k1 + offsetR,j - k2 + offsetC);
}
}
}
}
//根据边界条件获取A矩阵的元素
template
T GetA_Ele(int row,int col)
{
switch(Bc)
{
case zero: //索引超出界限认为0
if((row < 0)|(row > A_Row)|(col < 0)|(col > A_Col))
return 0;
case bound: //超出索引部分和边界值相等
if(row < 0)
row = 0;
else if(row >= A_Row)
row = A_Row - 1;
if(col < 0)
col = 0;
else if(col >= A_Col)
col = A_Col - 1;
return A[row][col];
case period:
while((row < 0)|(row >= A_Row))
{
if(row < 0)
row += A_Row;
else
row -= A_Row;
}
while((col < 0)|(col >= A_Col))
{
if(col < 0)
col += A_Col;
else
col -= A_Col;
}
return A[row][col];
default:
return T(0);
}
} 以上函数执行结果是:
1 4 8 12 16 19 15
4 14 26 37 48 56 43
7 22 37 48 59 67 51
10 30 48 59 70 78 59
12 35 55 66 77 85 64由于没有矩阵运行时库,并且算法相对简单,因此设置参数更麻烦。需要手动给出矩阵的行和列。此方法中的三个参数完全相同,完全相同,有效和MATLAB。此外,为了更方便的图像处理,提供了三个可选的卷积边界条件。由于A矩阵的值在卷积计算过程中可能超过索引,因此有必要使用GET方法进行封装。
为了使用MATLAB验证我们的算法,以下是BC = Zero;;,然后确定三种不同方法的计算结果是否与MATLAB中的计算结果相同。 MATLAB的相应代码如下:
clear
clc
a = [1,2,3,4,5;...
2,3,4,5,6;...
3,4,5,6,7;...
4 5 6 7 8];
b = [1 2 1;2 3 2];
c = conv2(a,b,'full')以上述简单的端口代码为前奏,我们可以编写一个更正式的转为模板,以便我们将来使用。相应的C ++类模板CONS使用方法如下(请参阅文章末尾的源代码):
#include "Eigen\core"
#include
#include "Conv.h"
using namespace std;
using namespace Eigen;
using namespace ConvSpace;
int main()
{
MatrixXd a(4,5);
MatrixXd b(2,3);
a << 1, 2, 3, 4, 5,
2, 3, 4, 5, 6,
3, 4, 5, 6, 7,
4, 5, 6, 7, 8;
b << 1, 2, 1,
2, 3, 2;
try
{
Conv myConv(a, b); //第一种调用形式
//Conv myConv(a, b,ConvType::Full,BoundaryConditon::Period); //不使用默认参数
cout << myConv.Eval() << endl; //直接输出结果
//const MatrixXd &r = myConv.Eval(); //第二种获取结果的形式
//cout << r << endl;
//Conv myConv; //第二种调用形式
//myConv.SetA(a);
//myConv.SetB(b);
//cout << myConv.Eval() << endl;
}
catch(ConvError ce)
{
cout<> c; //程序暂停
} 执行结果如下:
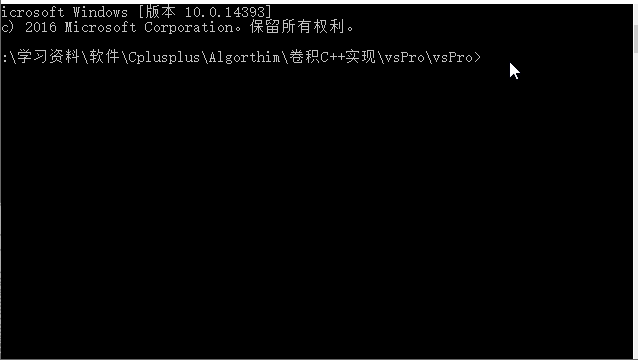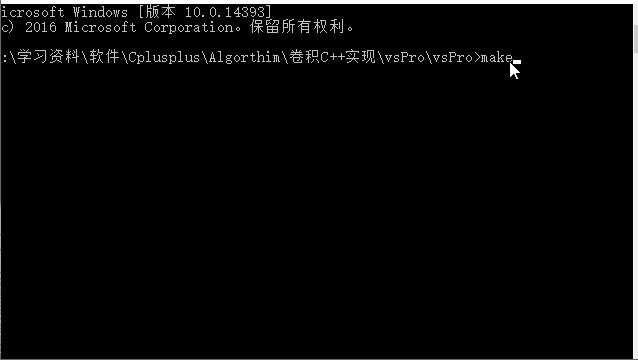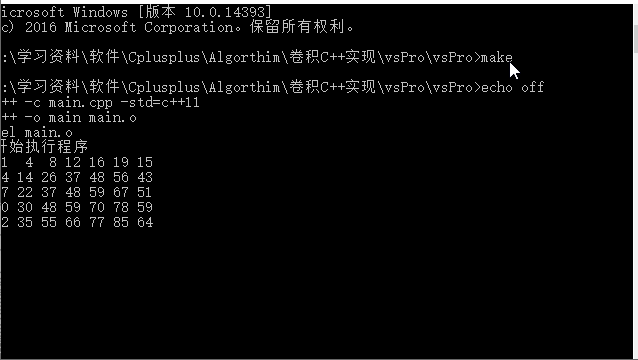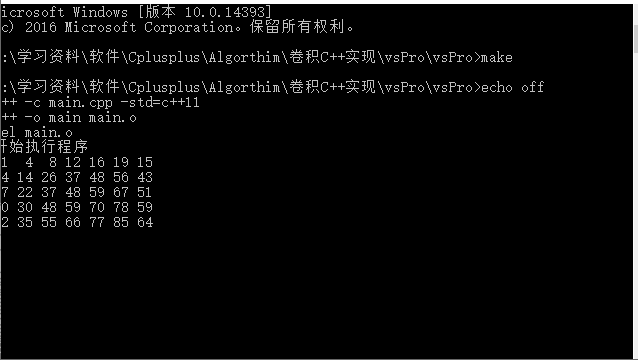
该算法需要使用EIGEN矩阵运行时库,因此需要包含与EIGEN相关的文件和名称空间。此外,该算法在Convspace名称空间中实现,因此必须在使用该函数之前包括名称空间和相关文件。
此功能通常有两种类型的调用。一种是给出构造函数中的卷积矩阵,然后执行计算。另一个是使用一个空构造函数,然后通过设定方法设置相关矩阵,最后计算。第一种方法更简单地调用如下:
Conv myConv(a, b); //第一种调用形式
cout << myConv.Eval() << endl; //直接输出结果 使用上述代码时,应将所有代码放在try语句块中,并捕获转换器异常。当参数配置错误或其他错误发生时,将抛出异常。检查例外的描述以确定异常的原因。
上面使用了默认边界条件零和默认卷积方法。当然,您也可以自己选择边界条件和卷积方法(如上所述)。
如前所述,在介绍该原理时,在MATLAB中有另一种形式的conv2呼叫,这是为了计算两个向量和一个矩阵的卷积。此算法在这里未实现。实际上,向量也是一个特殊的矩阵。有兴趣的学生可以在代码中完成此部分内容。最好共享完成的代码。
源代码
图像卷积的4个想法
从先前的卷积定义来看,我们可以发现将卷积的概念引入图像处理无法直接看到其物理意义,并且主要涉及以下三个移植问题:
它翻译了输入序列“正向”之一,该序列要求在计算某个点K的卷积结果时,您需要知道k+i“ time”的输入序列值。当将时间序列用作输入时,这通常是不可能的。
在图像卷积的说明中,我们可以知道,卷积实际上首先旋转卷积内核,然后乘以并将其添加到另一个矩阵中。由于它不是直接乘法和添加,因此滤波器操作员表达的物理意义很明显。
卷积通常在图像处理中具有“边界概念”。这个概念在数字信号处理中不存在,因为在数字信号的零状态下,线性系统没有输入,也没有输出。
从以上几点来看,我们可以看到,卷积的概念在推广到图像处理方面发生了巨大变化,这也使卷积更具含义。因为卷积的概念是在图像处理和实现完整的“本地化”中具有直观的物理含义。因此,我们可以稍微修改卷积的定义,并在图像处理中以更清晰的含义定义图像卷积如下:
相应的示意图如下:
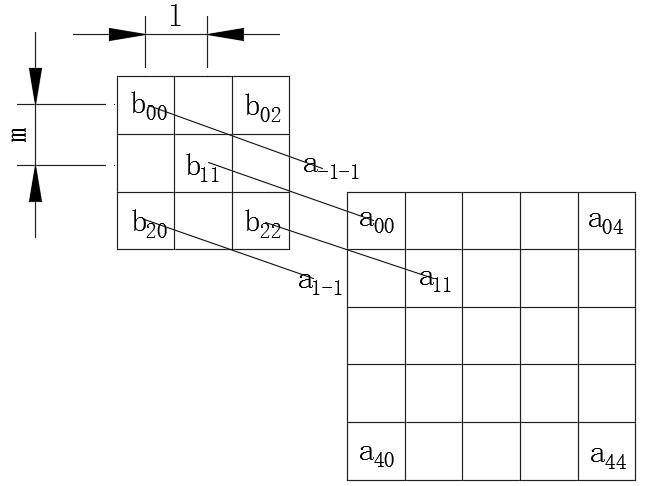
上面定义的图像卷积与阵列信号处理中的卷积略有不同。这样,将卷积的概念移植到图像处理中,并且不会逆转卷积内核。请注意,B矩阵的左上角是B(0,0)。此外,在乘法和加法过程中卷积内核的中心位置可以通过两个可调节的偏移L和M调节。以上图像卷积公式具有更直观的物理意义。
当然,有利弊。在数字信号处理中,我们对卷积的讨论已经得出了许多非常成熟的结论。因此,如果我们使用普通的卷积概念,则可以将这些讨论和结论直接用于图像处理中。例如,卷积等于频域中的乘积,卷积的换向定律和分配速率等。尽管上述卷积也可以通过讨论获得相似的属性,但毕竟它增加了很多工作量。
简而言之,有利弊。如果我们需要直观地在图像处理中使用卷积,则上述公式还可以帮助我们在某些方面理解基本的卷积公式。





