一维卷积、二维卷积、三维卷积具体应用

由于计算机视觉的流行，二维卷积的用途范围最广。因此，本文首先介绍了二维卷积，然后介绍了一维卷积和三维卷积的特定过程，并描述了它们各自的特定应用。

1。二维卷积

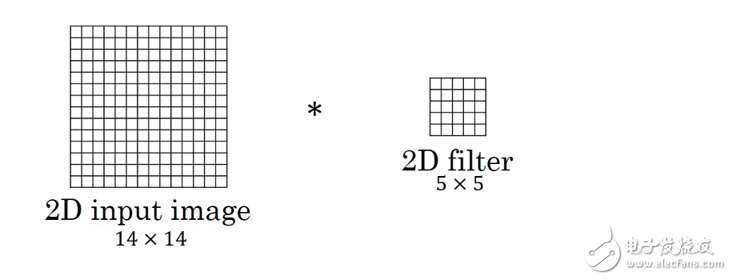
•图中的输入数据维度为14×14，滤波器大小为5×5。两者是卷积，输出数据维度为10×10（14-5 + 1 = 10）。

•以上内容没有引入通道的概念，也可以说，通道的数量为1。如果在二维卷积中输入的通道数将其更改为3，则输入数据维度（14×14×3）。由于卷积操作中过滤器的通道数必须与输入数据的频道数量相同，因此滤波器大小也将变为5×5×3。在卷积过程中，滤波器和数据分别沿通道方向进行了卷积，然后添加了卷积值，添加了3个数字值的10×10次，即执行3个数字值的10×10倍。

•以上是与1个过滤器数量的讨论。如果过滤器的数量增加到16个，即16个，大小为10×10×3，则最终输出数据维度将变为10×10×16。可以将每个过滤器分别执行卷积操作开yunapp体育官网入口下载手机版，并将每个过滤器分别固定在第三个方向上的每个卷积的输出（最终）。

•二维卷积通常用于计算机视觉和图像处理领域。

2。一维卷积

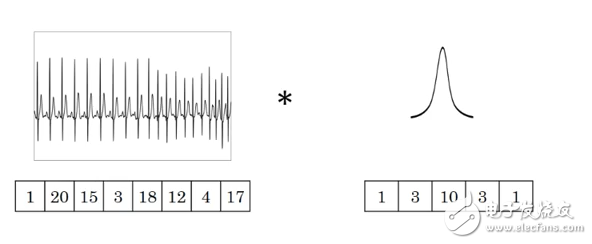
•图中的输入数据维度为8，滤波器尺寸为5。类似于二维卷积，卷积后的输出数据维度为8-5+1 = 48-5+1 = 4。

•如果过滤器的数量仍然为1，则输入数据的通道数量为16，即输入数据的维度为8×16。此处开yun体育官网入口登录app，通道的概念等于嵌入自然语言处理中，并且输入数据代表8个单词，每个单词的单词矢量尺寸为16。在这种情况下，数据仍然是5到5到5×5到5×5到5×5×5×5到5×5到5×5到5×。

•如果过滤器的数量为n，则输出数据维度将变为4×n。

•一维卷积通常用于序列模型和自然语言处理字段。

3。三维卷积

在这里开yun体育app入口登录，我们使用代数方法介绍了三维卷积，具体思想与一维卷积和二维卷积相同。

•假设输入数据大小为A1×A2×A3，通道号为C，并且过滤器大小为

f，即，滤波器尺寸为f×f×f×c（通道的尺寸通常不写），并且过滤器的数量为n。

•基于上述情况，三维卷积的最终输出为（a1-f + 1）×（a2-f + 1）×（a3-f + 1）×n。该公式对于一维卷积和二维卷积仍然有效，只有通过删除无关的输入数据维度就足够了。

•三维卷积在医疗领域（CT影响）和视频处理场（操作和性格行为的检测）通常使用。