勾股定理的应用

毕达哥拉斯定理的应用

----------------立体声图形中的最短循环问题

1。内容和内容分析

1。内容

使用毕达哥拉斯定理在三维图中解决两个点的最短问题。

2。内容分析

毕达哥拉斯定理是特别广泛使用的，并且使用毕达哥拉斯定理解决立体镜头中两个点的最短问题是本章经常遇到的一种问题。可以通过扩展立体图并将其转换为平面图，然后使用“线段公理”和“毕达哥拉斯定理”来解决这种类型的问题。

对本课程的探索是基于人们经常喜欢在现实生活中采取“快捷方式”的平面问题的研究，然后引导学生探索沿“弯曲的表面”和“折叠表面”的两个点的最短路径。探索过程应反映从“特殊到一般”的研究方法，同时让学生感受到“转型和转型”在解决实际问题中的数学思想的重要作用。

基于上述分析，可以确定，本课程的教学重点是：探索将三维图形扩展到平面数字的方法，并学习使用线段公理和毕达哥拉利亚定理以找到最短的距离。

2。目标和目标分析

（1）体验将三维数字转化为平面人物的探索过程，了解三维图形和平面图可以相互转化，感觉到从特殊到一般的研究方法，培养学生的动手能力和空间想象力，并使学生能够从感知的理解中实现飞跃。

（2）学会使用“线段公理”和“毕达哥拉斯定理”来找到并找到三维图中两个点之间的最短距离，并澄清“转化和转化”的数学思想是我们解决此类问题的基本意识形态方法。

3。诊断和分析教学问题

在初中的第一学期中，学生已经学习了线段公理，并且知道在飞机上，他们可以使用“两个点之间，线段是最短的”，以找到两个点之间的最短距离，然后找到这两个点之间的最短距离。但是，如果两个点沿着相同的弯曲表面或沿不同折叠表面的最短路径，则涉及空间中三维图的平面膨胀问题。但是，由于初中学生的二年级只学习简单的平面数字，因此三维数字受知识结构和认知能力的限制，并且他们的空间想象能力相对较差，因此很难解决这个问题。因此，在教学过程中，教师应指导学生自己练习，提高感知理解，了解三维人物和平面图的相互转换过程，然后解决沿“弯曲表面”和“折叠表面”的两个点的最短问题。基于上述分析，本课程的教学难度是：如何指导学生学习将三维图形扩展到平面图中，并确定沿“表面”和“折叠面”的两个点之间的最短距离。

4。分析教学支持条件

1。教师和学生使用自制的教学辅助工具 - 圆柱体，立方体，立方体，锥体等。亲自体验三维人物和平面人物的相互转变的过程，提高其空间想象力，并为学生从感知知识转变为理性知识奠定基础；

2。借助多媒体课程软件，动态演示了圆柱体，立方体和立方体的平面扩展过程，并进一步验证将三维图形扩展到平面图中的方法，从而使学生从感知理解到理性的理解实现了飞跃。

5。教学过程设计

1。查看旧知识和触发思维

简介：我们以前已经了解了毕达哥拉斯定理的相关知识。今天，我们将使用毕达哥拉斯定理来解决一种实际问题 - 三维图形中最短的距离问题。让我们首先看一个简单的问题。

有一个矩形的花床，有人避开角落并在花园里走一条路。问题：这样行走的理论基础是什么？他们只采取了几步？ （假设2个步骤为1米）

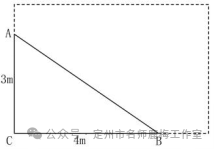
师生活动：教师使用课件来显示实用问题和抽象的几何模型来指导学生回答问题。学生通过分析回答问题，并解释他们的理论基础。

问题：在平面中，两个点之间的最短距离是连接两个点的线段的长度。如果两个点在弯曲的表面或折叠表面上，那么我们应该如何找到沿弯曲表面和折叠表面的最短距离？

设计意图：使用多媒体课程在生活中显示一个常见的“快捷方式”问题，以便学生可以回想起他们在初中第一年中学到的“线段公理”，并使用“毕达哥拉斯定理”来计算最短的距离，从而奠定了最短的距离，以在三维图中找到最短的距离。随后的质疑旨在指导学生进一步思考并激发学生的好奇心和好奇心。

2。按一层进行进步，探索新知识

活动1：

如图所示，有一个圆柱，周长为18米，高度为12米。底部有一个蚂蚁。它想在上下A的B点A点吃食物。围绕圆柱侧爬行的最短距离是多少？

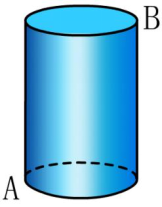
教师活动：多媒体显示问题。老师首先启发学生使用矩形纸质纸形成圆柱体，观察到圆柱体的侧面是弯曲而不是平坦的，并强调了点A和点B在圆柱体侧面的特定位置。问一个问题：如何找到沿圆柱体侧面A点到B点的最短距离？学生回答说，将圆柱体的侧面扩展到计划图中，然后使用“线段公理”和“毕达哥拉斯定理”来解决问题。老师要求学生绘制计划扩展图，计算最短的距离并显示。然后，老师使用多媒体来显示圆柱体的侧面扩展过程，以验证学生方法的正确性。

设计意图：教师指导学生制作自己的圆柱体开元ky888棋牌官网版，并观察到圆柱体的侧面是弯曲的表面。目的是增强学生的感知理解，并避免“飞行人”的发生直接连接空间中的A和B点B。学生亲自体验绘画和计算和展示它们的过程，从而提高了他们对学习的兴趣。老师使用多媒体来验证学生方法的正确性，从而进一步增强了他们在学习中的自信心。

变体一

如图所示，如果点B直接在点A上方，那么蚂蚁在圆柱侧面爬行的最短距离是多少？

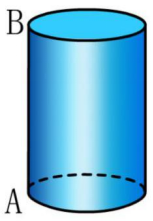
教师学生的活动：教师更改上述问题，将B点更改为直接在A上方，并找到了蚂蚁在圆柱侧面爬行的最短距离。根据解决上述问题，学生绘制计划扩展图，计算最短的距离并显示它。然后，老师使用多媒体来验证其正确性。

设计意图：通过这个问题，学生可以将解决方案进一步加深到沿“表面”的两个点的最短距离。他们仍然需要将三维数字扩展到计划图中，然后解决它。

变体2

如果B直接在点A上方，并且蚂蚁在圆柱体侧面的侧面爬行了两个星期，那么此时最短的距离是多少？爬行三周呢？那n周呢？

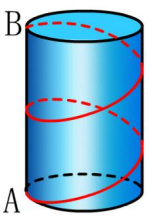
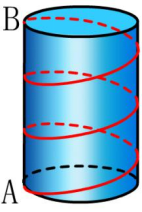
教师学生的活动：老师总结了前两个问题：一个是蚂蚁在圆柱体周围爬行半个星期，另一个是蚂蚁在圆柱体周围爬行了一个星期。在此基础上，进一步的指导学生找出蚂蚁在圆柱周围爬行两三个星期之间的最短距离吗？学生使用自制的圆柱体来研究，讨论和交流，绘制飞机扩展图，计算和显示。老师还使用自制的教学辅助工具和多媒体课程来演示以验证学生结果的正确性。

设计意图：通过这个问题，学生将被指导考虑深入思考问题，学会质疑并找到解决问题的解决方案，以提高学生自己分析和解决问题的能力。

后续问题：如果蚂蚁在相等距离的圆柱体周围爬行，他应该如何找到他的最短距离？

教师学生的活动：在教师提出问题之后，学生们根据解决先前问题并回答N周内最短距离的方法探索规则。

设计意图：扩大学生的思维和培养学生的总结和总结能力。

实践

如图所示，有一个圆柱，周长为10 cm，高度为14厘米。在距底部1厘米的点，有一个蚂蚁。如果它想在距顶表面1厘米的点在距顶面1厘米，而与点A相对，那么沿圆柱体侧面爬行的最短距离是多少？

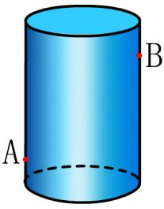
师生活动：教师使用多媒体课程来显示问题，学生独立思考，绘制图片，计算和展示。

设计意图：测试学生对所学知识的理解和掌握，并将他们学到的知识付诸实践。

3.不同的思考和探索新知识

活动2

如图所示，已知立方体边缘长2厘米。一种小昆虫想从A点到对面的点沿立方体的表面喂食。最短的距离是多少？

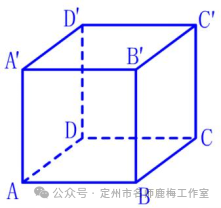
教师学生活动：沿着“弯曲表面”的两个点的最短距离可以通过展开成平面图来解决。那么，如何解决沿“折叠表面”的两个点的最短距离呢？教师使用多媒体来显示多维数据集的几何形象，并指导学生分别在立方体的表面上观察A和C。然后，教师和学生使用自制教学辅助工具从A点到点探索Cube表面的不同扩展方法。学生在黑板上绘制六个扩展图，并计算最短的距离。教师指导学生观察，分析和得出结论。

设计意图：通过探索特殊的立方体的平面膨胀方法 - 立方体，让学生感觉到沿着“折叠表面”上两个点的最短距离，您必须首先将“折叠的表面”展开到飞机上，以便可以计算出最短的距离，以提高学生的感知意识，以阐明较晚的问题，以解决问题，并在两个问题上解决问题，并在两个问题上求解了两个点的基础。

问题：如果多维数据集的边缘长度是3厘米，则从点A到C的最短距离是多少？那4厘米呢？ CM呢？

设计意图：通过疑问，指导学生发现和总结规则。

已经发现，如果立方体的边缘长度为a，则最短的距离沿着立方体的表面从A点到点Cˊ沿cˊ点。

变化

如图所示，有一个长度，宽度和高度为5 cm，4 cm和3 cm的矩形体。如果您沿着矩形的表面从A到Cˊ，最短的距离是多少？

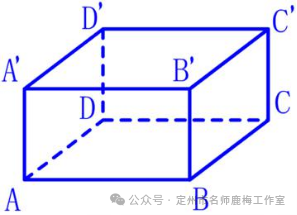
教师学生的活动：根据先前的问题，教师将立方​​体更改为矩形，指导学生发现展开矩形的方法，并鼓励学生找到最短的距离。学生独立思考，分组讨论和交流，展示和解释。

设计意图：通过研究一般立方体，我们将进一步探索沿“折叠表面”解决这两个点的最短路径，增强学生的理性理解，并为随后的发现和摘要规则奠定基础。

问题：如果矩形体的边缘长度为1cm，2cm和3cm，那么此时从点A到点C的最短距离是多少？如果边缘长度为6厘米，7厘米，12cm怎么办？如果边缘长度为a，b，c（其中a> b> c）怎么办？

设计意图：通过验证几组其他边缘长度，学生最终将接受并总结规则。

发现：

如果长方体的长度，宽度和高度分别为厘米，b厘米和c厘米和a> b> c，则最短的距离沿着立方体的表面从点A到点c。

实践

如图所示，在片段AB的第三个段AB（a）的第三相等点有一个蚂蚁，在B'C段的中点F处有一粒水稻。蚂蚁从点E从点E到米粒F沿着Cuboid的表面爬行的最短距离是多少？

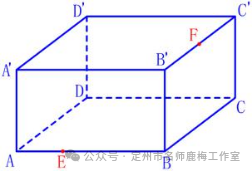
教师学生的活动：教师使用多媒体课程来显示问题，学生独立思考开元棋官方正版下载，绘制图片，计算和显示不同的方法。

设计意图：测试学生对他们早些时候学到的知识和规则的掌握。学生使用各种方法来解决问题并扩大思维方式。

4。组织知识并优化结构

概括

解决立体声图形中最短路径问题的方法：

（1）将三维数字转换为平面图；

（2）使用“毕达哥拉斯定理”和“两个点之间的线段的最短公理”来解决问题；

（3）对于矩形体，如果其边缘长度满足A> b> c，则最短的距离在同一平面中不在两个点。

师生的活动：教师和学生一起回顾本课程的内容，并将解决方案总结到三维数字中两个分之间的最短距离。

设计意图：通过摘要，法律和方法摘要，优化学生的知识结构，并使学生能够实现理性理解的飞跃。

5。分配家庭作业并扩展思维

（1）如图所示，圆柱玻璃容器高10厘米，周长为30 cm。距离外部下底表面的点S 3厘米处有一个蚂蚁。距蚂蚁对面的圆柱容器上底部的开口距离1厘米处有食物。这只蚂蚁吃食物的最短距离是什么？

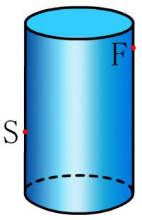
设计意图：结合沿“弯曲的表面”和“折叠表面”这两个点的最短问题，以进一步训练学生的思维方式，并提高学生分析和解决问题的能力。

（2）如图所示，众所周知，圆锥体的舱底为OA = 8 cm，底圆的半径为r = 2 cm。如果一只小昆虫沿着锥侧爬行一个星期，然后返回到A点，那么小昆虫爬行的最短距离是多少。

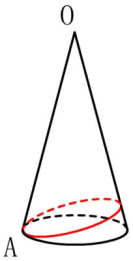
设计意图：设计不同类型的三维图形，扩大学生的思维方式，培养学生发散思维的能力，并让学生感到“一切变化都不会与根源分开”的原则。

vi。对象检测设计

1。如图所示，在山脊长度为10 cm的立方体的顶点A处有一个蚂蚁。现在它即将爬向顶点B。众所周知，蚂蚁的速度为1 cm/秒，并且速度保持不变。我问蚂蚁是否可以在20秒内从A升至B。

示意图设计意图：检查三维图中沿“折叠表面”的两个点的最短距离。

2。如图所示，有一个高度为2.1m的木支柱，周长为40厘米。为了在准备元旦聚会时营造一个节日的气氛，老师要求小敏将丝带均匀地从圆柱的底部到顶部的顶部均匀开yunapp体育官网入口下载手机版，直到它直接在起点上方。小敏至少需要准备多长时间？

设计意图：在三维图中沿两个点的“表面”的最短距离的解决方案。

3。如图所示，有一个矩形位点，AB = 2M，AD = 1M，如图所示，有一个矩形木制块堆叠。块的边缘EF与矩形位点的边缘AD平行，并且块的前视图为正方形，侧面长度为0.2m。蚂蚁需要从A到C的最短距离超过米。 （准确0.1m）

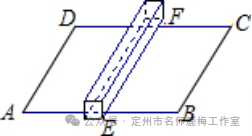
设计意图：三维图形和平坦图形中两个点之间最短距离的综合解决方案。

感谢您的阅读和喜欢。您可以单击此页面上的蓝色字体“ Lumei著名教师工作室”，也可以直接识别上面的官方帐户名片以增加关注，并查看已上传到主题类别中的相关内容。每天，您都会不时收到有意义的数学信息。如果您周围有初中老师，孩子或父母，请转发并推荐他们。我希望有需要更多的人能看到它！