数学王朝—伯努利家族,塑造了数学史的进程,彻底改变了科学面貌

想象一个场景,每个人都坐在餐桌旁,在家庭聚会上讨论微积分。在您了解伯努利家族的传奇之前,这听起来可能很不寻常。这个家庭被称为数学界的王朝,他们对数学的深刻理解和贡献彻底改变了科学的格局。这引发了一个想法:伯努利家族的知名度仅仅是因为他们的才华,还是只是碰巧生活在快速数学发展的黄金时代?该家庭培养了至少八位著名的数学家,包括雅各布,约翰和丹尼尔·伯诺利,微积分领域的先驱,微分方程,概率理论和流体力学。接下来,这个家庭成员的生活和成就以及他们如何塑造数学和物理学的早期发展。
雅各布·伯诺利(1654-1705)
在17世纪末,雅各布·伯诺利(Jacob Bernoulli)以对数学的深刻洞察力而闻名,这是伯努利家族的杰出人物。他首次展示了数学常数E,展示了他的非凡智力。雅各布的主要作品ARS Cuniptandi完全改变了概率理论的研究方法,并成为该领域的里程碑。
雅各布出生于一个经营香料业务并在巴塞尔担任议员的家庭,最初在巴塞尔大学攻读神学和哲学学位。然而,正是雷恩·笛卡尔(RenéDescartes)和布莱斯·帕斯卡(Bryce Pascal)的作品引发了他对数学的热情。这种热情最终导致他于1687年成为巴塞尔大学的数学教授,在此期间开yun体育app入口登录,他与当时的数学大师进行了深入的学术交流,包括戈特弗里德·莱布尼兹(Gottfried Leibniz),克里斯蒂安·霍根斯(Christian Huygens)和gualilmo de lopital。

他最著名的作品是概率理论和组合科学,尤其是他的著作《猜想的艺术》,该书于1713年出版。在这本书中,他介绍了期望的概念,大量定律,伯努利分布和伯努利实验。他还证明了二项式定理适用于任何理性指数,并得出了许多重要的公式和身份,涉及二项式系数,例如pascal三角形,范德蒙特身份和chu-van der mont身份。
雅各布·伯诺利(Jacob Bernoulli)还为变异的计算做出了重要贡献。变异方法是一种数学理论,研究如何找到某些数量的最大或最小值。他解决的第一个著名问题是最快的下线问题,它涉及在重力作用下找到对象在两个点之间降低路径的最快曲线。他还解决了等待数周的问题,也就是说,找到由给定长度包围的最大面积曲线。他将其名称为“ Lemniscate”并研究其属性的“ 8”曲线命名为“ 8”曲线。
雅各曾经说过,
我用爪子认出了狮子。
我通过他的爪子认出狮子。
我们通常通过智力的表现来确定一个人的才能,但是对于雅各布·伯诺利(Jacob Bernoulli)来说,可能会质疑他的成就是真正的天才还是仅仅是因为他专门致力于数学,这是它在崛起时的领域。雅各布于1705年去世开元棋官方正版下载,享年50岁,死亡原因是结核病。他被埋葬在巴塞尔大教堂的走廊中,墓志铭刻有“ Eadem Mutata Resurgo”,这意味着“尽管有变化,我仍然像往常一样恢复。”他的墓碑上刻有一个诱人的象征,是他在数学领域取得成就的象征。

约翰·伯诺利(John Bernoulli)(1667–1748)
雅各布的弟弟约翰·伯诺利(John Bernoulli)是家庭中有才华的人物的典范。尽管他似乎在一开始就处于哥哥的出色成就上,但约翰展示了他在数学方面的才华和创新,尤其是在微积分领域。他的个性包含了挑战精神,他甚至有勇气通过信件来挑战数学巨人莱布尼兹。
约翰成为伯诺利家族的成员,不仅继承了他哥哥在巴塞尔大学担任数学教授的地位,而且还在格罗纳根大学,巴黎科学院和圣彼得堡帝国学院担任重要职务。他与莱布尼兹(Leibniz)的密切合作以及与艾萨克·牛顿(Isaac Newton)的比赛。
约翰·伯诺利(John Bernoulli)在微积分的早期发展中发挥了核心作用,他对微积分的了解主要来自莱布尼兹(Leibniz)。他成功地将微积分的原理应用于广泛的领域,例如分析颗粒运动,研究摆动,探索悬浮链的行为以及了解光弯曲的方式。约翰在数学的几个关键领域中表现出了深厚的专业知识,尤其是在他处理可变分离的技能方面,使用微积分方法来指数函数以及应用有限的差异方法。
他的重要成就之一是在微积分的基本定理中发现了一个基本概念。该定理揭示了积分和导数之间的直接连接,即,函数的集成过程可以通过其衍生物反向操作。
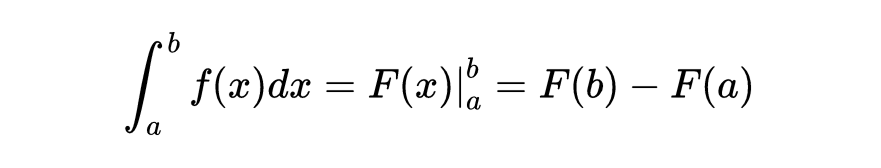
约翰·伯诺利(John Bernoulli)还与他的兄弟雅各布(Jacob)一起为变异方法做出了贡献。他独立地解决了速度下线问题,并提出和解决了等距问题,该问题寻找特殊的曲线,以使粒子从任何初始位置落到最低点所需的时间是相同的。他还介绍了欧拉 - 拉格朗日方程,这是寻找方程式极值的主要工具。
约翰不仅专注于微积分。他还涉足数量理论,几何,代数和分析。他证明E是一个不合理的数字,是发明了极性坐标,并用它们来研究固定在旋转臂上的点的运动产生的曲线。他还介绍了曲线家族的信封的概念,以及曲线的外部曲率线。
约翰也是著名的导师。他导演了下一代数学天才,例如莱昂哈德·欧拉(Leonhard Euler),让·莱昂·达拉姆帕克(Jean-Leon Darrampell),皮埃尔·路易斯·莫普特图(Pierre Louis Moppertui)和约瑟夫·路易斯·拉格朗(Joseph Louis Lagranges)。更不用说他的儿子丹尼尔(Daniel)和约翰二世(John II),他们也继承了数学才华。
约翰·伯诺利(John Bernoulli)于1748年去世,享年80岁。他的墓志铭写着:“阿奇米德,牛顿和他”(阿基米德斯,牛顿等)。
丹尼尔·伯诺利(Daniel Bernoulli)(1700-1782)
当我们谈论丹尼尔·伯诺利(Daniel Bernoulli)时,我们立即想到了科学家,他以解释液体速度和压力之间关系的伯努利原理而闻名。他对流体动力的贡献是极其开创性的,但这是否意味着他仅继承了以前的伟人和家庭的智慧?实际上,丹尼尔的成就不是孤立的事件,而是伯诺利家族对数学和科学的长期投资和热情的自然延续。他的作品“流畅的动态”不仅是展示个人才华,而且是对家人对科学探索的热情的高潮。
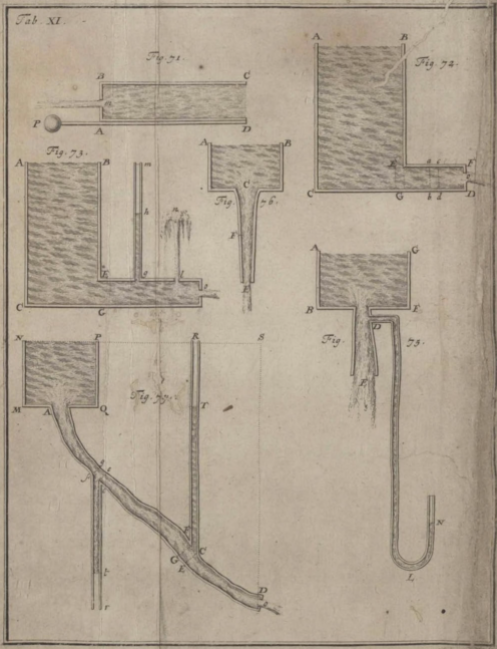
丹尼尔·伯诺利(Daniel Bernoulli)是一位数学家和物理学家,以他在流体动力学和概率理论方面的工作而闻名。他在巴塞尔大学学习医学和数学,并获得了博士学位。 1721年。他还前往意大利,法国和俄罗斯,在那里他与莱昂哈德·奥拉(Leonhard Oula),阿莱西斯·克莱拉特(Alessis Claylaut)和克里斯蒂安·戈德巴赫(Christian Goldbach)等许多著名科学家见面并合作。 1725年,他在圣彼得堡大学获得了数学教授的职位,到1733年,他在巴塞尔大学的教授中深入研究了解剖学和植物学。
丹尼尔(Daniel)最著名的作品是流体动力学,于1738年出版。在本书中,他将能量和动量的保护原则应用于流体流动,并衍生了以他命名的Bernoulli方程,该方程将压力开yun体育官网入口登录app,速度和流体高度相关联。
他还解释了文丘里效应的现象,其中压力降低,随着流体穿过管道的狭窄部分,速度会增加。他还研究了人体中血液的流动以及空气阻力对弹丸运动的影响。
他还为概率理论和统计理论做出了重要的贡献,尤其是在数学对社会和自然科学的应用方面。他开发了预期效用的概念,该措施是根据其发生的可能性及其有效性来衡量风险结果价值的措施。他使用这个概念来解决圣彼得堡悖论(由他的堂兄尼古拉斯·伯诺利(Nicholas Bernoulli)发明),这是一个游戏问题,涉及无限的期望,但期望有限。他还介绍了标准偏差的概念,以衡量分散数据集围绕其平均值旋转的方法。

丹尼尔(Daniel)于1782年去世,享年82岁。他被埋葬在巴塞尔大教堂的回廊中,靠近父亲和叔叔。他的墓志铭写着:“他是Bernoulliorum中最伟大的”(Ille Fuit Maximus Bernoulliorum)。
伯努利家族的其他成员

尼古拉斯·伯诺利(Nicholas Bernoulli)是伯努利(Bernoulli)家族中的杰出人物,有时被错过,他在概率理论和统计学方面的工作至关重要。他与皮埃尔·雷蒙德·德·蒙特莫特(Pierre Raymond de Montemott)关于概率问题的深入交流不应被视为普通的学术对话,而是类似于充满智慧的比赛。
随着18世纪的时间过去了,伯努利家族在数学领域的影响并没有减少。家庭中有约翰二世,丹尼尔二世和约翰三世等继任者。他们继续保持家庭的数学活动,好像这是其祖先成就的一系列续集。但是,有一个关键的讨论点:这些继任者是开辟了新的数学和理论领域并展现了真正的创新领域,还是只是根据现有知识进行一些小的调整和补充,即重复前几代的工作而没有重大进展?
最终,伯努利家族在科学领域留下了深远的影响,这是由于其非凡的才能和有利的环境。他们留给世界的不仅是一系列数学公式和物理定律。更重要的是,他们证明了自己对杰出成就的渴望,在科学探索过程中的竞争以及他们在不断探索知识方面的持久性。这种对知识探索和卓越努力的持续追求可能是构成伯努利家庭传奇人物真正本质的要素。



