解决50%高中物理问题的理论
如果您被要求告诉您高中力学中最重要的理论是什么?我相信,任何研究高中物理学的人都会给出自己的答案,其中大多数答案包括:牛顿的第二定律,动能定理,机械节能法,动量定理和势头保护法。为什么?因为这是高中物理和力学的基本框架理论。如果您完全了解这些理论,那么您将有基本的保证解决高中的50%问题。
通过在同一图片中表达这五种理论(如下所示),您可以清楚地看到它们之间的关系。对于任何物理问题,我们将在时空中考虑它。在牛顿的第二定律中,工作与动能变化之间的关系是通过在太空中积累力来获得的,而机械能保护定律则通过极限力(重力或弹性力)来进一步获得。脉冲和动量变化之间的关系是通过时间积累力量获得的,而动量的保护定律是通过在系统上作用的限制力(内力)进一步获得的。
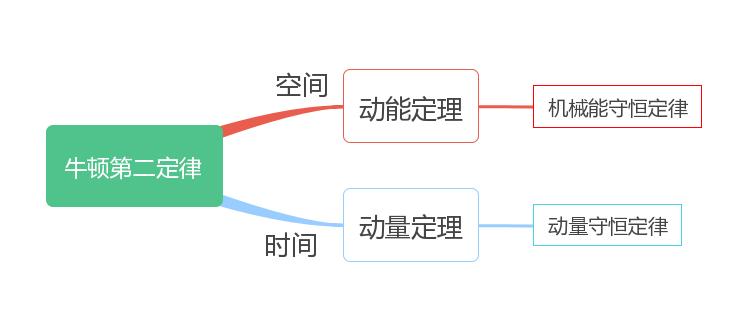
下面我们逐一分析了这五种机制及其关系中最重要的理论。
1。牛顿的第二定律
牛顿第二定律在力学上的重要立场是不言而喻的。无论哪个高中物理教科书是哪个版本,第一本书都必须基于牛顿的第二定律作为核心。整个课程的排列是首先研究均匀速度,然后是纽顿运动定律的线性运动。基本逻辑是首先讨论物理量的加速度A,然后是物理量F,最后通过加速度和力。
这座桥将
和
这两个物理量是相关的。
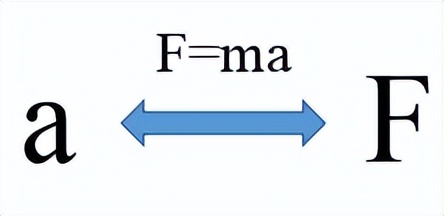
牛顿的第二定律具有以下属性:
1。矢量
在牛顿的第二定律中
和
所有都是向量,质量
作为标量,表达式中的相等符号不仅代表数学相等的关系关系,而且在方向上也具有相同的含义。因为
和
方向是一致的,因此在某些问题中,当对象的速度为零时,我们可以根据对象的加速度计算相应的力。例如,以下问题适用于牛顿第二定律的向量性质。
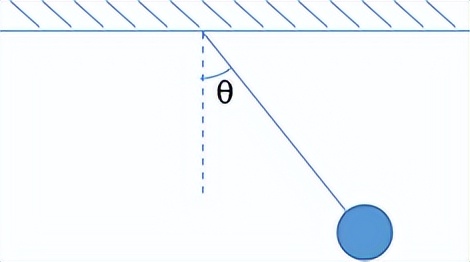
如图所示,质量是
球静置。找出:释放球时绳索的拉力是什么?
由于球将在释放后的圆形运动中移动,因此其切向加速度必须垂直于绳索。释放瞬间的速度为零,因此中心力加速度也为零。这样,球的加速度方向在释放时垂直于绳索,即联合力的方向垂直于绳索。知道关节力和绳索拉力的方向,重力的大小和方向,很容易找到绳索拉力的大小,因为
。
2。瞬间
和
这是一对同时存在和消失的物理量,也就是说,这两个物理量是瞬时加速度及其同时受到的力。我们将此特性用于解决一种常见的问题 - 有效突变问题。由于问题相对常见,因此我不会在这里举例。
3。因果关系
牛顿的第二定律表达
实际上,我们看不到它
和
可以从“物体加速度的大小与力成正比,与物体质量成反比,加速度与力的方向相同。”这就是对象产生加速的原因。在牛顿第二定律的验证实验中,我们通过控制变量方法分别研究了它
重量m之间的关系通过改变张力而保持不变
测量不同的
,它还表明,这两个物理量之间的关系是力的变化导致加速度的变化,即力是原因,加速度是结果。
4。身份
当应用牛顿的第二定律分析对象的运动时,我们的压力分析的第一步是确定研究对象。为什么?由于牛顿第二定律中的三个物理量与同一对象相对应,因此国际单位系统用于在同一惯性参考系统中进行分析。还应强调的是,在力分析过程中,您必须专注于研究对象进行分析。例如,在使用整体方法研究板模型的过程中,一些学生总是将多个对象的总质量与单个对象的质量一样,这会导致加速度计算错误或力计算中的错误。
5。独立
由于牛顿的第二定律是向量,因此其本质是数学中提到的矢量,我们可以以以下形式编写它:
就是说
方向上的力只能产生
沿方向加速
方向上的力只能产生
在方向上加速,两个方向上的加速度和作用力不会互相影响。想一想一个问题:为什么在研究投掷身体运动时,可以将物体的运动分解为两个垂直方向进行研究?原因在于这种性质。
牛顿的第二定律通常用于解决应用中的两种主要问题。众所周知,一个人寻求加速力,另一种是寻求加速。质量通常是已知的,很少有问题能够找到质量。但是,应该注意的是,这里提到的已知条件不一定告诉您它们直接在问题中,而是可以通过其他条件来计算的隐式已知条件。在适合应用牛顿第二定律的问题中,大多数对象都在统一改变速度运动,包括统一改变线性运动和均匀改变的速度曲线投掷身体(投掷身体运动)。为了进行定量分析,基本上考虑了某个瞬时或特殊位置的相关问题。例如,当在垂直平面上执行可变加速度循环运动时开yun体育app入口登录,对象必须计算与最低点(或等效最低点)和最高点(或等效最高点)相关的物理量。
2。动能定理
在分析动能定理之前,我们考虑了两个问题:
首先,我们为什么要定义
第二,为什么动能定义为
?
在回答这两个问题之前,让我们分析一个具体示例:
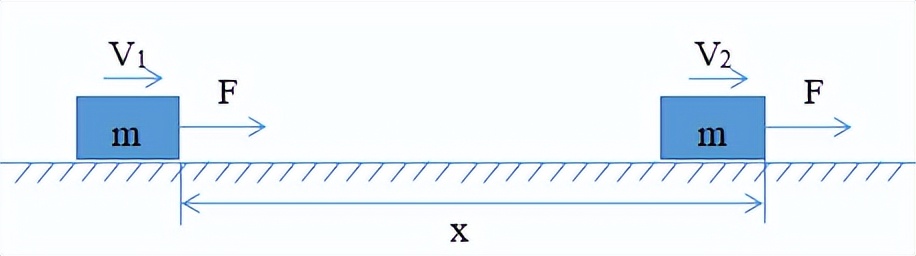
如图所示,质量是
对象正在拉动
在光滑水平平面的作用下,初始速度为
,最终速度是
,位移是
。从牛顿的第二定律和统一改变速度线性运动的定律,我们可以获得:
我们定义:
完成对象的工作,
对于物体在特定时刻或位置的动能,可以得出结论:
也就是说,对象在对象上接收的外力完成的工作等于对象动能的变化。您需要注意的是
和
不在同一条直线上,那么工作的表达是
,可以理解为
,也可以理解为
,现在
和
朝着相同方向的物理量或
分解为
向方向或
分解为
向方向。
就物体动量的变化而言,应注意的是,最后状态的动能必须减去第一个状态的动能。
目前,我们可以回答一开始提出的两个问题,因为我们已经介绍了牛顿第二定律和统一改变线性运动的新法律。我们为该法律提供了著名的动能定理,而在定理中出现的两个物理量分别命名为锣和动能。可以将动能定理与儿童进行比较。我们不会在孩子出生之前先命名孩子,因为孩子的性别和出生时间不确定,因此没有办法先命名。
尽管动能定理是根据均匀变化的速度线性运动引入的,但其应用范围不限于线性运动范围,并且曲线运动也适用。我们可以从显微镜的角度考虑这一点。对于任何弯曲的运动,我们都可以将运动分解为许多小部分
,每个小片段都可以视为线性运动:
使用动能定理解决了两种类型的问题。一种是根据已知条件计算外力完成的工作,然后计算初始状态或最终状态的速度;另一个是根据已知条件来计算动能的变化,然后计算外力完成了多少工作或某些力量完成了多少工作。第一个问题涉及解决方案方法,包括恒定力进行工作的解决方案方法,即可变力进行工作。以恒定的力量进行工作相对简单。根据工作的定义计算就足够了。要在可变力中进行工作,您需要掌握特殊的方法,例如微元素方法,图像方法,平均方法,转换方法等,并使用这些特殊方法来计算可变力量中的工作以表达工作,然后与动能定理进行相关计算。
3。机械能保护定律
在分析机械能源保护定律之前,我们首先要看两种情况:
1。只有重力才能工作
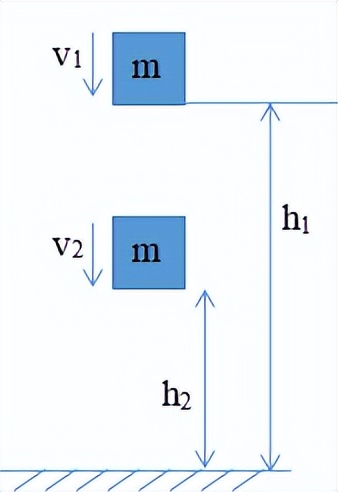
如图所示,一个质量是
地面物体的高度是
当速度为
,仅在重力到地面高度的作用下
以速度为
,在此过程中,根据动能定理,有:
定义:重力势能
,上述公式被组织并变形为:
2。只有弹性工作
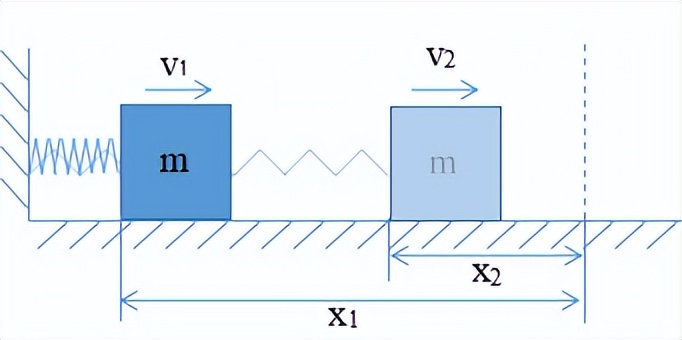
一种品质是
光滑水平平面上物体的刚度系数为
初始速度是
,最终速度是
弹簧变形变量是
,,,,
,由于弹簧力是一种可变力,而力与位移之间的关系是线性关系,因此可以使用平均方法或图像方法来轻松计算弹簧力对物体完成的工作:
根据动能定理,您可以获得:
定义:弹性势能
,然后可以将上述公式分类为:
可以从上面的两个示例中可以看出,当仅重力确实起作用或仅弹性力确实起作用时,势能变化和动能的总和为零。如果弹性势能减少,
和重力势能
它被归类为势能,这意味着可以获得机械能保护定律:
或者
在推理过程中,我们可以看到只有重力或弹性力才能在一个物体上起作用,而所涉及的能量仅是三个能量:重力势能,弹性势能和动能。因此,在使用机械能保护定律之前,我们必须使用以下三个条件来确定机械能量是否保存:
除了首先判断机械能量是否保存外,我们还必须确定该物体运动的第一和最后状态的势能和动能如何根据问题表达。机械能保护定律仅集中于第一个和最后一个州。无需准确分析和计算对象如何在第一个状态和最后一个状态之间的其他时刻移动。
iv。动量定理
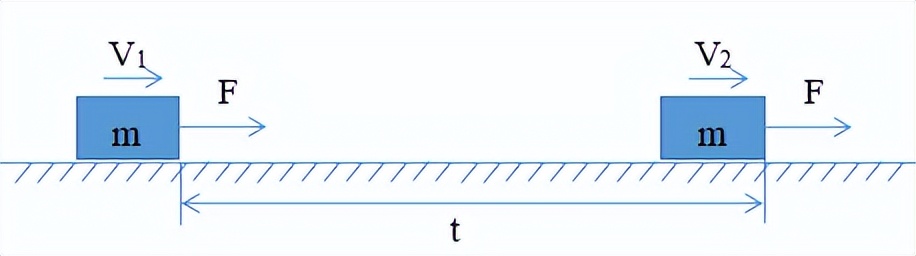
如图所示,质量是
对象正在拉动
在光滑水平平面的作用下,初始速度为
,最终速度是
,运动时间是
。从牛顿的第二定律和统一改变速度线性运动的定律,我们可以获得:
我们定义:冲动
,势头
,然后您可以获得:
也就是说,外力的冲动等于对象动量的变化。冲动是向量,它也是过程数量,动量也是向量。由于速度是瞬时数量,因此动量也是瞬时数量,对应于特定矩。从方程式的角度来看,该方程式所涉及的物理量是向量,因此该方程是向量方程,我们还可以将其分解为两个方向:
动量定理不仅可以解决恒定力下的运动学问题,而且还适用于可变力下的运动学问题,尤其是与电磁诱导和流体问题有关的问题,只能从动量的角度来分析溶液。
5。势头保护定律
接下来,我们分析如何使用动量定理推断动量保护定律:
如上图所示,质量是
A对象的初始速度是
,质量
初始速度是
B对象发生碰撞后,速度变为
,,,,
,假设在碰撞过程中A到B的平均力为
,b上B的平均力
,碰撞时间是
,使用动量定理分别分析A和B,您可以获得:
将两个公式添加到:
再次
和
对于相互作用,
,所以
现在:
更简洁的表格可以直接表示为:
尽管动量保护定律用于派生过程中,但我们的结论仍然适用于二维或三维空间。在推理过程中,除了两个对象之间的相互作用力外,系统中其他力的影响不被考虑。这是因为对象的组合力是其他力的零,因此在应用动量定理时不必考虑它。在使用动量保护之前,您必须首先确定从以下三个方面保守动量,即
势头保护定律仅需要在大学入学考试中进行一维要求。需要使用势头保护定律的问题具有明显的特征,例如碰撞,爆炸,而不是在一定方向上受到外力的影响。
第六,五个主要理论的应用
以前的重点是从理论角度分析各种定理,法律及其关系。这些法律和定理是我们解决机械问题的最重要工具。也就是说,当我们解决机械问题时,我们主要是从牛顿第二定律,功能关系和动力的三个角度来思考。
牛顿的第二定律通常用于解决恒定力下的线性运动问题,功能关系和动量更适合。它不仅可以解决线性运动的问题,还可以解决恒定力或可变力下的曲线运动问题。许多学生总是觉得当他们遇到复杂的力学问题时,他们不知道如何开始。对于拥有丰富经验和扎实基本技能的学生,他们可以一目了然地看到要分析的角度。对于经验不足的学生来说,总共只有三个思维维度,并且一个一个一个一个核对他们可能不是可行的方法。让我们举一个例子:
如图所示,在具有磁感应强度的均匀磁场中,将质量的导体杆放在光滑的水平轨道上。两个轨道之间的距离是,左侧电阻值的电阻在两个轨道之间连接。导轨和导体杆之间的电线的电阻被忽略。考虑到右侧导体杆的初始速度,从开始到最终停止的导体杆的位移是多少?
在解决问题之前,我们需要考虑解决问题的思维方向并确定要考虑的维度。导体杆在磁场中移动以切割磁电感线以产生诱导的电动力
,并且由于导轨,导体杆和电阻形成闭合电路,因此将产生诱导的电流
,如果导体杆中有诱导的电流,则将其在磁场的左侧受到安培力。
,然后您将减慢练习。由于导体杆接收到的安培力与速度有关,因此当速度降低时,安培力也会降低,因此导体杆将执行减少加速度的减速运动。
图像是曲线,我们不能使用高中知识来解决曲线下的区域 - 导体杆的位移,因此牛顿的第二定律肯定不会可行。那么使用动能定理呢?不可能。尽管我们知道一开始和结束时的速度,但我们知道动能的变化,但是安培力量的工作确实在改变力而作用,而力量的幅度与速度有关开元棋官方正版下载,而不是与流离失所有关,因此我们无法表达工作。这样,我们只能从第三维的角度考虑解决这个问题。
当使用动量时,我们可以判断系统动量绝对不能保存,因此我们只能使用动量定理进行分析:
设置在很短的时间内
内部开yun体育官网入口登录app,导体杆的瞬时速度为
,左将的力量是:
从动量定理中,我们可以获得:
在整个运动中,将所有时间元素添加在一起:
也就是说,导体杆从其初始位置到最终停止的位移是
。
在这一点上,对高中物理学机械问题的问题解决框架的分析已经结束。我们需要做的是总结基于这些框架的常见模型,解决问题的方法和解决问题的技术,并在练习时故意从这些角度考虑。如果上述所有要求都可以在高水平上完成,那么所有机械问题基本上都可以解决!



