【整体解读】勾股定理:几何学中的一颗明珠
毕达哥拉斯定理:几何珠
文字/朱Yuehong
您是否听说过“控制洪水”的故事?他如何成功管理水? Zhao Shuang在“ Zhou Feng Suan jing笔记”中写道:“ Yu控制的洪水,脱离了河流,看着山脉和河流的形状开yun体育app入口登录,确定了高度和底部,消除了压倒性的灾难,缓解了床垫的麻烦,以及向东泛滥,这是毕达哥拉斯的起源。定理。不足为奇吗?在本章中,我们将欣赏几何形状的闪亮珍珠 - 毕达哥拉斯定理。
一,
明智地阅读历史。
寻找“毕达哥拉斯定理”的原型
在中国古代,当人们以直角弯曲手臂时,靠近肩膀的部分被称为“钩子”,靠近手掌的部分被称为“大腿”。通常,“钩”的长度小于“链”的长度。在西州西部王朝的早期,Shang Gao在与周的对话中提到“ Go guang san,Gang Si耕种四,Gang Si Centivation Five五”。后来的几代人称其为“ Go Sanli,四个,四个,五个”,这是毕达哥拉斯定理的原型。
对于3²+4²=5²,这是毕达哥拉斯定理的特殊情况,也是中国毕达哥拉斯定理的最早记录。为了追踪根本原因,毕达哥拉斯定理是我国古代数学发展的重要起源。中国传统数学文化的本质,例如处方和方程式的艺术,与毕达哥拉斯定理密切相关(有兴趣的学生可以检查“ Zhoufeng隶属关系”)。毕达哥拉斯定理的发现并不容易,毕达哥拉斯定理的证明更加惊人。数千年来,人们一直被其魅力所吸引开yun体育官网入口登录app,并对毕达哥拉斯定理的证明产生了浓厚的兴趣。目前,它是世界上最著名的证明方法的数学定理之一。
二,
穿越过去和现在,
探索“毕达哥拉斯定理”的结构
我们知道三角形有六个元素(三个侧面和三个角)。研究三角形是研究每个元素之间的关系。我们经常遵循从一般到特别的规则。通常,三角形的特殊边缘是同步的三角形,而特殊角度是直角三角形。本章从生命中提取正确的三角模型→绘制并总结并验证毕达哥拉斯定理(边缘关系)→图形转换,以了解毕达哥拉斯定理的判断方法→恢复生活并使用毕达哥拉斯定理解决问题。
具体而言,我们将建立一个知识结构,如图1所示,这也反映了本章的结构美。

图1
三,
将您学到的知识付诸实践,
欣赏“毕达哥拉斯定理”的魅力
毕达哥拉斯定理在生活中广泛使用,并在中学入学考试问题中发光。例如,如图2所示,梯子AB长25m,梯子的底端距离墙壁7m。 (1)如果梯子的顶部滑动4m,则水平滑动梯子的底部有几米? (2)如果梯子从图3的起始位置向下滑到图4,而下端水平滑动,则A和B之间的关系是什么? (3)在A点和B点的滑动过程中,您还能发现哪些其他问题?请探索。
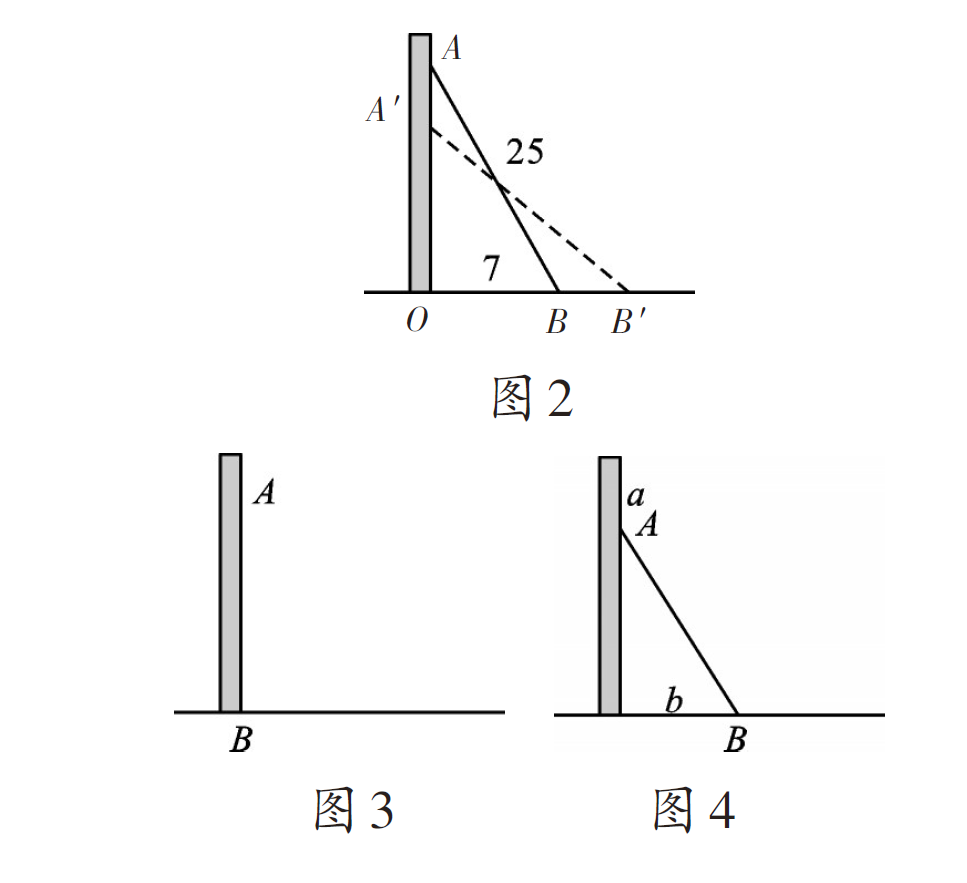
分析:将实际问题转换为数学模型后,我们可以使用毕达哥拉斯定理列出方程。
1。假设水平方向是滑动XM,并且从毕达哥拉斯定理中,获得OA = 24,∴oa'= 20,并且从毕达哥拉斯定理中获得(7+x)+20²=25²,获得x1 = 8,获得x1 = 8,
x2 = -22(放弃);
2。从毕达哥拉斯定理,我们得到(25-a)²+b²=25²,解决方案为a²-50a+b²= 0;
3。问题:滑动过程中的a = b吗?探索:如果a = b开元ky888棋牌官网版,请替换a²-50a+b²= 0,获取a1 = 0,a2 = 25,因此当a = 0或25时,a = b,即,将梯子放在地面上的地面在滑动过程中开始和最后,当a = b时a≠b。
作为古老的数学定理,毕达哥拉斯定理包含了古代中国的深刻文明。它的出现和发展在古代数学文化的发展中起着重要作用。学生,让我们更接近“毕达哥拉斯定理”,并感觉到它的丰富含义!
作者单位:江苏省Taizhou医疗高科技区(Gaogang District)的教师发展中心




