pg下载官方认证 遗传算法的matlab代码_遗传算法实际应用
大家好,又见面了,我是你们的朋友全栈君
目录
1、遗传算法流程
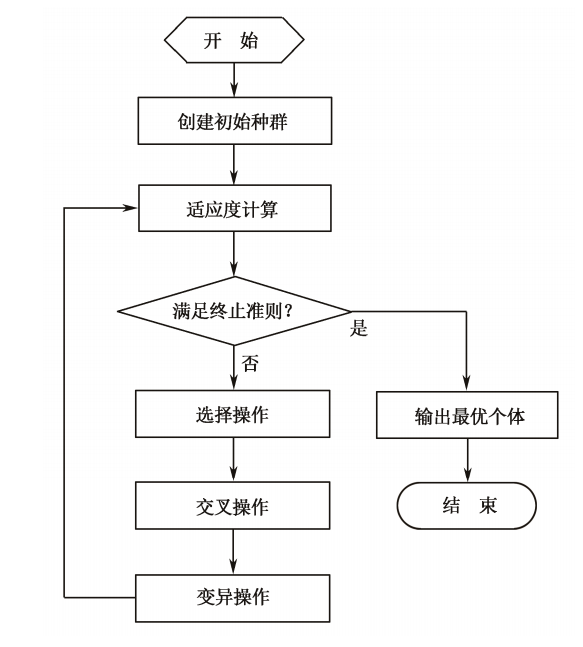
遗传算法的运算流程如下图所示:
具体步骤如下:
(1)进行初始化操作,将进化代数计数器 \(g\) 设置为 \(0\),同时设定最大进化代数为 \(G\),通过随机方式生成 \(NP\) 个个体,以此来作为初始群体 \(P(0)\)。
(2)针对于其中个体方面去展开评价,要对群体 \(P(t)\)里每一个个体的那种适应的程度高低好坏进行计算 。
(3)针对此给出选择运算,把选择算子施加于群体之上,依据个体的适应情况作出判断,按照特定的规则或者方法,从其中挑选出一些具备优良特质的个体,使其能够被遗传到下一代群体之中 。
首先,存在交叉运算这一行为。接着,要把交叉算子施加于群体之上。对于被选出来的成对个体而言,开始以某一个概率实施交换它们彼此之间部分染色体的操作。最后,从而产生出新的个体、。
针对被选中的个体(属于特定群体),把变异算子发挥作用于所述群体予以处置(注意到这个群体是特定目标包含其中的相应群体),此时选取特定概率针对该个体的某一个或者相应的某一些基因值去改变,变更为剩下的其他等位基因(变更类型明确为其他等位基因这种特定类型)。特定群体 \(P(t)\),历经选择、交叉以及变异运算步骤之后,进而形成出新且承接的下一代群体 \(P(t+1)\)。确定求出得到的这个对象的适应度数值,并且依据适应度给定具体数值(其数值给定依据为适应度)进行排序处理,以此来准备开展下一轮的遗传操作(操作类型明确为遗传操作这种专门类型)。
第一种情况,假设存在终止条件判断,当出现 \(g\) 小于等于 \(G\) 的状况时,会将 \(g\) 的值更新为 \(g\) 加上 \(1\) ,随后转移到步骤(2);第二种情况,若 \(g\) 的值大于 \(G\) ,那么会把在这个进化过程当中所获取的拥有最大适应度的个体当作最优解进行输出,以此来终止计算。
2、关键参数说明(1)群体规模 \(NP\)
遗传优化的最终结果以及遗传算法的执行效率会受到群体规模影响,群体规模 \(NP\) 太小时,遗传优化的性能通常不会太好,采用较大群体规模能减小遗传算法陷入局部最优解的机会,然而较大群体规模意味着计算复杂度较高,一般而言 \(NP\) 取值在 \(10\cdots200\) 之间 。
(2)交叉概率 \(P_c\)
交叉概率 \(P_c\)pg下载,对交叉操作被使用的频度起到控制作用,较大的交叉概率呀,可增强遗传算法开辟新的搜索区域的能力呢,然而高性能的模式遭到破坏的可能性就增大啦,要是交叉概率太低呢,遗传算法搜索可能会陷入迟钝状态哟,一般情况下,\(P_c\)取值在 \(0.25~1.00\) 。
(3)变异概率 \(P_m\)
遗传算法里,变异是辅助性搜索操作,其主要目的是维持群体多样性,一般低频度变异可预防群体内重要基因可能遗失,高频度变异会使遗传算法趋近纯粹随机搜索,通常\(P_m\)取值在\(0.001\)到\(0.1\)之间。
(4)进化代数 \(G\)
遗传算法运行结束条件由终止进化代数 \(G\) 来表示,作为一个参数,它意味着遗传算法运行到指定进化代数便停止运行,接着会把当前群体里的最佳个体当作所求问题的最优解而去输出,取值方面,通常要视具体问题来定,\(G\) 可在 \(100~1000\) 之间 。
实例3.1,是运用MATLAB进行仿真,求解一元函数之极值,借助遗传算法,3、。
例2.1,运用标准遗传算法求取函数\(f(x)=x + 10\sin(5x)+7\cos(4x)\) 的最大值,当中\(x\) 的取值范围有所属情况。这是一个具备多个局部极值的函数,其函数值图形呈如下图示。
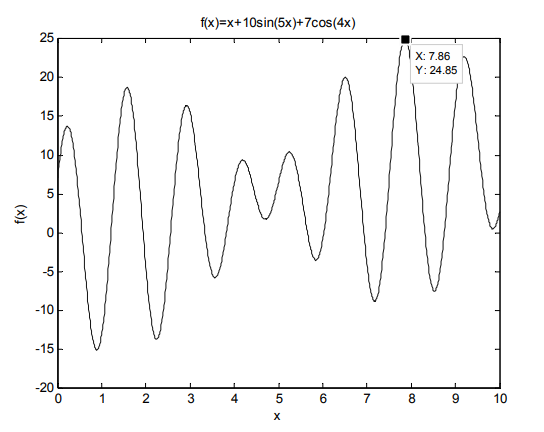
解:仿真过程如下:
将种群数目设置成50且这里的50用NP表示,把染色体二进制编码长度设定为20且此20用L表示,把最大进化代数确定为100且该100用G表示,将交叉概率设置成0.8且这个0.8以P_c表示,再把变异概率设置成0.1且此0.1用P_m表示 。
先产生初始种群,将那种二进制编码给转换成十进制,去计算个体适应度值,并且进行归一化;接着采用以轮盘赌为基础的选择操作、与基于概率相关的交叉和变异操作,从而产生新的种群,还要把历代当中的最优个体留存于新种群之内,之后方才能够进行下一步遗传操作。
1. 首先要做的是,判断一下,是不是满足终止条件。 2. 要是满足了终止条件,那么就要结束搜索过程,然后输出优化值。 3. 要是不满足终止条件,那就得继续进行迭代优化。
优化完了之后,它的适应度进化曲线是像下面这个图所展示的那样,优化的结果呈现为x等于7.8567,函数f(x)的最大值是24.86 。

MATLAB 源程序如下:
用标准的、遗传方面的算法,去求取,那名为函数极值的东西,。
初始,设置其参数,使其处于一种特定状态,这种状态即为初始化的参数设定 。
clear all; %清除所有变量
close all; %清图
clc; %清屏
NP = 50; %种群数量
L = 20; %二进制位串长度
Pc = 0.8; %交叉率
Pm = 0.1; %变异率
G = 100; %最大遗传代数
Xs = 10; %上限
Xx = 0; %下限
f = rand(NP,L); %随机获得初始种群
遗传算法,进行循环,呈此般状况,这般模样,如此情形,这般态势,如此状况呢。
for k = 1:G
把二进制进行解码,使其成为在定义域范围以内的十进制,%%%%%%%%%。
for i = 1:NP
U = f(i,:);
m = 0;
for j = 1:L
m = U(j)*2^(j-1)+m;
end
x(i) = Xx+m*(Xs-Xx)/(2^L-1);
Fit(i) = func1(x(i));
end
maxFit = max(Fit); %最大值
minFit = min(Fit); %最小值
rr = find(Fit==maxFit);
fBest = f(rr(1,1),:); %历代最优个体
xBest = x(rr(1,1));
适应度等于,适应度减去最小适应度的差,除以最大适应度减去最小适应度的差,以此来进行归一化适应度值的计算 。
依据轮盘赌方式的,用于复制的操作,%%%%%%%%%%%%,%%%%%%%%%%%%%。
sum_Fit = sum(Fit);
fitvalue = Fit./sum_Fit;
fitvalue = cumsum(fitvalue);
ms = sort(rand(NP,1));
fiti = 1;
newi = 1;
while newi <= NP
if (ms(newi)) < fitvalue(fiti)
nf(newi,:) = f(fiti,:);
newi = newi+1;
else
fiti = fiti+1;
end
end
%%%%%%%%%%%%%%%基于概率的交叉操作%%%%%%%%%%%%%
for i = 1:2:NP
p = rand;
if p < Pc
q = rand(1,L);
for j = 1:L
if q(j)==1;
temp = nf(i+1,j);
nf(i+1,j) = nf(i,j);
nf(i,j) = temp;
end
end
end
end
%%%%%%%%%%%%%基于概率的变异操作%%%%%%%%%%%%%%
i = 1;
while i <= round(NP*Pc)
h = randi([1,NP],1,1); %随机选取一个需要变异的染色体
for j = 1:round(L*Pc)
g = randi([1,L],1,1); %随机选取需要变异的基因数
nf(h,g) =~ nf(h,g);
end
i = i+1;
end
f = nf;
f(1,:) = fBest; %保留最优个体在新种群中
trace(k) = maxFit; %历代最优适应度
end
xBest; %最优个体
figure
plot(trace)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')
%%%%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%%%%
function result = func1(x)
fit = x+10*sin(5*x)+7*cos(4*x);
result = fit;
end3.2 遗传算法求解旅行商问题(TSP)
例如 2.3 所提及的旅行商问题,也就是 TSP 问题。假有着这样一个情况,存在一位旅行商人,其目的是要去拜访涵盖全国 31 个行政区域内首位城市的省会之地,他面临着需要甄选一条行进路线的状况,此路线有着相应限定,即每个城市在所限定的情境下只能被去拜访一回,不仅如此,更重要的是最终还要返回到一开始出发的那个城市。对于他要进行的路径选定,是有着明确要求的,那便是:在所能够获取到相关可能资讯的所有路径里,要挑选出路程处于最小数值状态的那一条路径。而全国 31 个省会城市各自所具备的坐标是 。
对于这些数字组合,比如,分别有着这样那样的值情况,像1304对应2312这样的一种具体搭配值情况,数目的一种对应值情况展现,1304的这种值状况与2312的那种值状况搭配,算是一种特定形态的数值对应关系;又比如3639有着自身的那种状况,它与1315形成这种特定的数值对应状况;4177、2244之间有着特属于它们独特呈现的一种数值对应关系;3712、1399这种数值之间有着其自身独有的一种对应呈现;3488相关于1535有着特定形态的数值对应关联,3488对应1535这样的一种对应态势;3326关联着1556构建出其特有的一种数值对应关系存在;3238与1229之间具有特属于它们那种形态的数值结合对应态势;3007和1970之间有着自身别具一格呈现的数值对应关系;2562、1756这种数值组合有着其特定风格的对应联系态势;2788、1491这两个数目之间具有其独特的数值对应关系态势呈现;2381匹配着1676有着自身特有的一种数值对应联系;1332、695之间有着别具一格的数值对应态势;3715、1678这种数值配对存在着其特有的一种对应关系状态;3。
解:仿真过程如下:
进行初始化操作,种群数目设定为二百,染色体基因维数设定为三十一,最大进化代数设定为两千 。
先产生初始种群,然后计算个体适应度值,也就是路径长度,接着采用基于概率的方法选择用于操作的个体,再针对选中的成对个体,随机性地交叉所选中的成对城市坐标,目的是确保交叉后路径里每个城市仅仅到访一次,之后针对选中的单个个体,随机性地交换其对称城市坐标当作变异操作,进而产生新的种群继而进行下一次遗传运作。
(3)判断是否满足终止条件:若满足,则结束搜索过程pg下载,输出优化值;若不满足,则继续进行迭代优化。
优化后的路径以及其适应度进化曲线如下图所示:
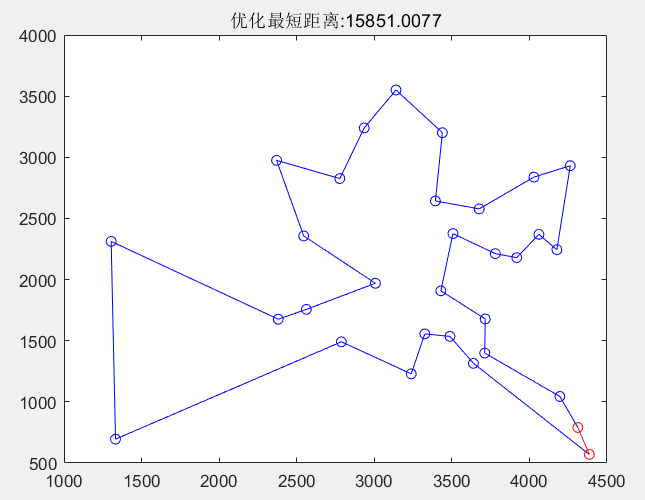

MATLAB 源程序如下:
遗传算法对 TSP 问题予以解决,是通过特定方式,在众多可能路径中,不断筛选、优化,从而找到较优路径,进而解决该问题 。
clear all; %清除所有变量
close all; %清图
clc; %清屏
C等于,由1304与2312组成的,数对,3639与1315的数对、4177跟2244那个数组,又再是3712以及1399的数对,还有3488和1。
一组数字呈现为,先是3238与1229,接着是4196 与1044,再是4312和790,然后是4386以及570,随后是3007跟197。
可以这样理解为,存在这样一系列的数对,分别是,2788与1491作为一组数对,接着是,2381与1676构成一组数对,再接下来时,1332对应着695成为一组数。
3780对应2212,3676对应2578,4029对应2838,4263对应2931,3429对应1908,3507对应2376,...
将这些数字组合,分别是,包含3394与2643的一组,又有3439和3201的一组,还有2935以及3240的一组,再有3140跟3550的一组,另外是。
2370 2975]; %31 个省会城市坐标
N等于C的第一维大小,这是TSP问题的规模,也就是城市的数目 。
D = zeros(N); %任意两个城市距离间隔矩阵
%%%%%%%%%%%%求取,任意两个城市之间,距离间隔的矩阵%%%%%%%%%%%%%%。
for i = 1:N
for j = 1:N
将D(i,j)定义为,先计算C(i,1)减去C(j,1),使其结果进行第二次方运算,接着计算C(i,2)减去C(j,2),也将其结果进行第二次方运算。
end
end
NP = 200; %种群规模
G = 2000; %最大遗传代数
f = zeros(NP,N); %用于存储种群
F = []; %种群更新中间存储
for i = 1:NP
让表示索引的变量i所对应的那一行元素,等于随机从从总数为N的范围内进行无重复抽取后排列得到的结果,进而以此方式随机生成初始种群 。
end
R = f(1,:); %存储最优种群
len = zeros(NP,1); %存储路径长度
将fitness设定为全零数组,其维度为NP(数量)乘1,用于存储经过归一化处理后的适应值 。
gen = 0;
%%%%%%%%%%%%%%%%%遗传算法,进行重复循环%%%%%%%%%%%%。
while gen < G
%%%%%%%%%%%%%%%计算路径长度%%%%%%%%%%%%%%%%
for i = 1:NP
len(i,1) = D(f(i,N),f(i,1));
for j = 1:(N-1)
len(i,1) = len(i,1)+D(f(i,j),f(i,j+1));
end
end
maxlen = max(len); %最长路径
minlen = min(len); %最短路径
%%%%%%%%%%%%%%%更新最短路径%%%%%%%%%%%%%%%
rr = find(len==minlen);
R = f(rr(1,1),:);
%%%%%%%%%%%%%%计算归一化适应值%%%%%%%%%%%%%%
for i = 1:length(len)
fitness(i,1) = (1-((len(i,1)-minlen)/(maxlen-minlen+0.001)));
end
%%%%%%%%%%%%%%%%%选择操作%%%%%%%%%%%%%%%%
nn = 0;
for i = 1:NP
if fitness(i,1) >= rand
nn = nn+1;
F(nn,:) = f(i,:);
end
end
[aa,bb] = size(F);
while aa < NP
nnper = randperm(nn);
A = F(nnper(1),:);
B = F(nnper(2),:);
%%%%%%%%%%%%%%%交叉操作%%%%%%%%%%%%%%%
W = ceil(N/10); %交叉点个数
p = unidrnd(N-W+1); %随机选择交叉范围,从 p 到 p+W
for i = 1:W
x = find(A==B(1,p+i-1));
y = find(B==A(1,p+i-1));
temp = A(1,p+i-1);
A(1,p+i-1) = B(1,p+i-1);
B(1,p+i-1) = temp;
temp = A(1,x);
A(1,x) = B(1,y);
B(1,y) = temp;
end
%%%%%%%%%%%%%%%%%变异操作%%%%%%%%%%%%%
p1 = floor(1+N*rand());
p2 = floor(1+N*rand());
while p1==p2
p1 = floor(1+N*rand());
p2 = floor(1+N*rand());
end
tmp = A(p1);
A(p1) = A(p2);
A(p2) = tmp;
tmp = B(p1);
B(p1) = B(p2);
B(p2) = tmp;
F = [F;A;B];
[aa,bb] = size(F);
end
if aa > NP
F = F(1:NP,:); %保持种群规模为 NP
end
f = F; %更新种群
f(1,:) = R; %保留每代最优个体
clear F;
gen = gen+1;
Rlength(gen) = minlen;
end
figure
for i = 1:N-1
绘制,从,数值 C 中,对应索引 R(i) 的第一个元素,与,数值 C 中,对应索引 R(i + 1) 的第一个元素,所构成的点对,以及,数值 C 中,对应索引 R(i) 的第二个元素,与,数值 C 中,对应索引 R(i。
hold on;
end
绘制,将,[C(R(N),1),C(R(1),1)],作为,横坐标,把,[C(R(N),2),C(R(1),2)],当作,纵坐标,使用,'ro-',样式,标识,进行,plot,操作;。
设置标题,其中冒号连接的内容为,将最短距离最小化之后的数值转换为字符串,再与特定字符串拼接而成的内容 。
figure
plot(Rlength)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')4、遗传算法的特点
遗传算法乃一种并行、高效、全局搜索的方法,此方法是通过模拟生物于自然环境里的遗传以及进化的过程逐渐形成,它主要存在以下这些特点:
遗传算法把决策变量的编码当作运算对象,这种针对决策变量的编码处理形式,致使于优化计算进程里能够效法生物学里染色体以及基因等概念,去模拟自然界中生物的遗传跟进化等的机理,便利地运用遗传操作算子pg下载官方认证,尤其是对于一些仅有代码概念却没有数值概念或者极难存有数值概念的优化问题来说,编码处理形式更展现出了其独特的优越之处。
(2) 遗传算法是直接将目标函数值当作搜索信息的,它仅仅运用由目标函数值变换得来的适应度函数值,便能够确定进一步的搜索方向以及搜索范围了,然而它并不需要依靠目标函数的导数值之类的其他一些辅助信息。在实际应用里存在着许多函数是无法或者很难去求导的,甚至是根本就不存在导数,对于这类目标函数的优化以及组合优化问题而言,遗传算法则展现了其极为显著的优越性,原因在于它成功避开了函数求导这一障碍 。
(3)遗传算法运用多个搜索点的搜索信息,其对最优解的搜索进程,起始于众多个体构成的初始群体,并非单一的个体,针对这个群体展开的选择、交叉、变异等运算,产出新一代群体,其中涵盖众多群体信息,这些信息可防止搜索不必搜索的点,相当于多搜索了些点,这是遗传算法独具的一种隐含并行性 。
遗传算法是一种基于概率的搜索技术,它属于自适应概率搜索技术,其选择、交叉、变异等运算都是以概率方式来进行的,这增加了搜索过程的灵活性。虽然这种概率特性会使群体中产生一些适应度不高的个体,但是随着进化过程推进,新群体中总会更多地产生出优良个体。与其他一些算法相比,遗传算法的鲁棒性让参数对其搜索效果的影响尽可能小。
遗传算法有自组织特性,还有自适应特性,也有自学习特性等。当利用进化过程获取信息自行组织搜索时,适应度大的个体生存概率较高,且能获得更适应环境的基因结构。同时,遗传算法具备可扩展性,容易同别的算法相融合,进而生成综合双方优势的混合算法。



