pg下载 内容特别硬！初中数学的万能工具勾股定理深度梳理！

今天内容特别硬核！希望大家认真看，对数学学习特别有帮助！

勾股定理属于初中数学里的 “万能工具”，关键之处在于它运用最为广泛，且跨领域价值是最高的，整个知识体系能够依照 “核心优势 — 跨领域关联 — 应用场景 — 基础拓展” 这四层逻辑来展开。

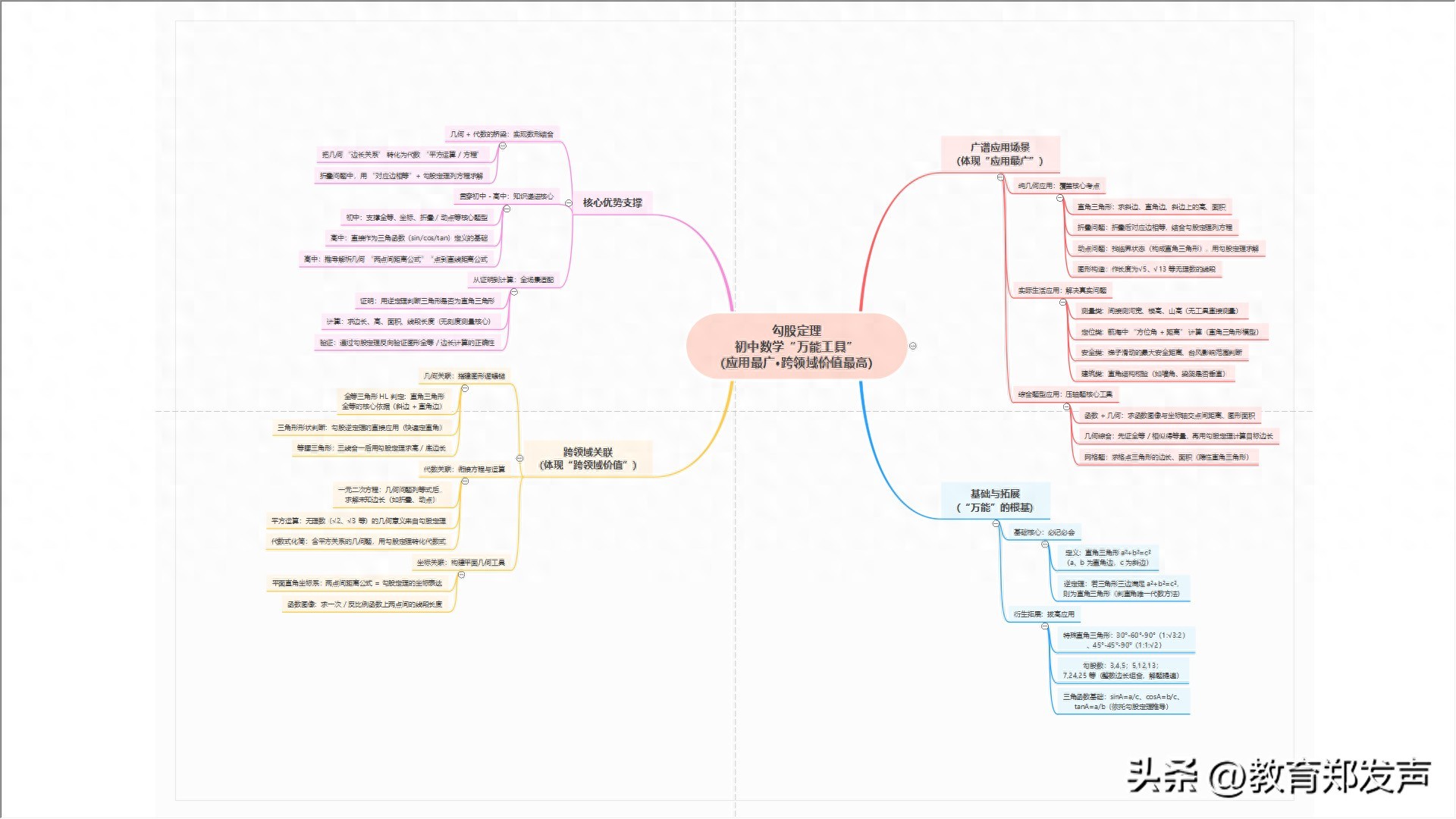
其核心优势呈现于三点，其一，把几何跟代数予以打通，可把边长关系转变为平方运算或者方程，就像在折叠问题里，借助对应边相等加上勾股定理去列出方程求解；其二，在初高中得以贯穿，于初中对全等、动点等核心题型起到支撑作用，在高中直接构成三角函数定义以及两点间距离公式的推导基础；其三，适配于全场景，既可以凭借逆定理对直角三角形做出判断，又能够去求边长、面积，还能够验证计算的正确性。

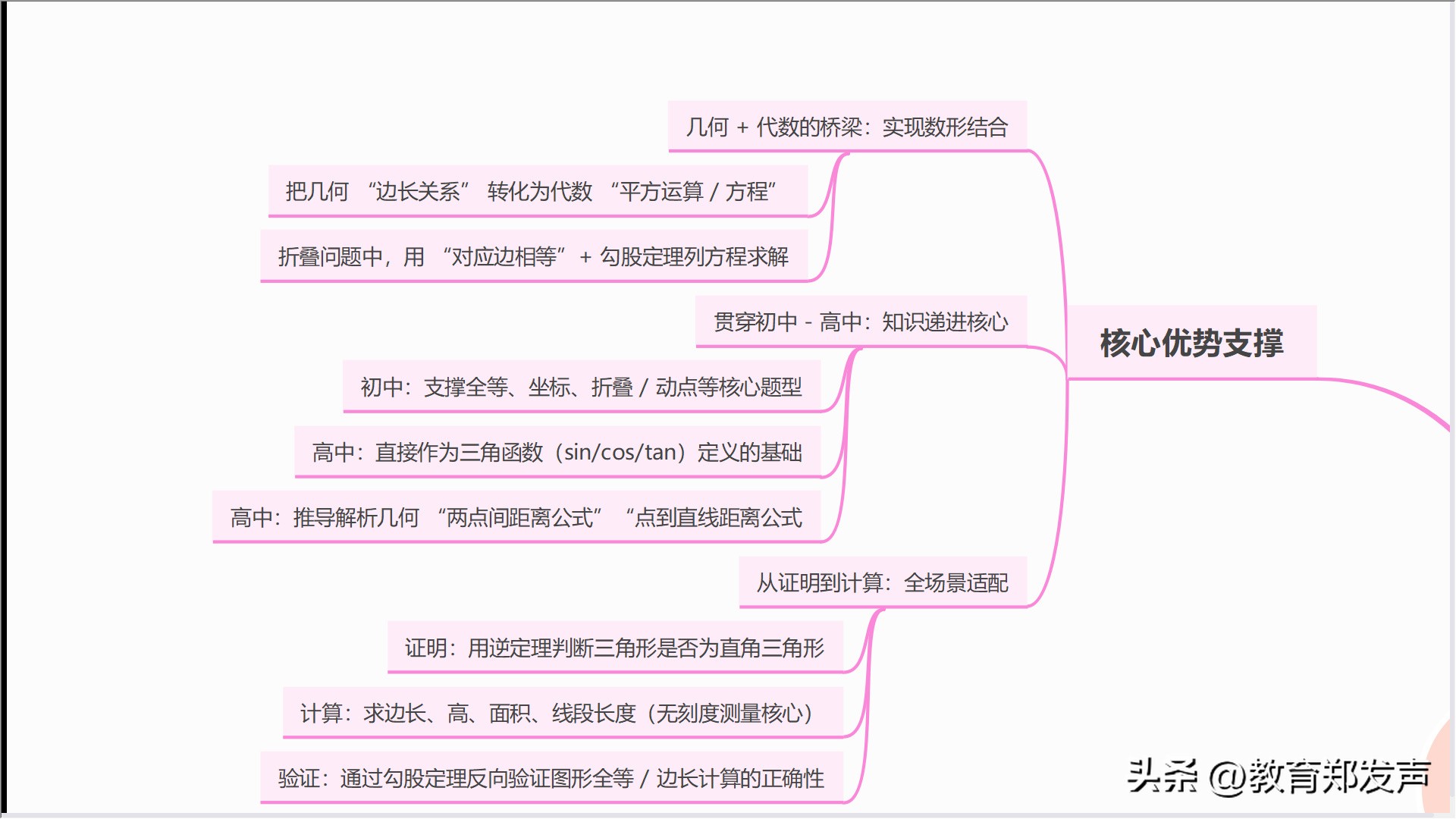
因为存在跨领域关联，所以它“无处不在” ，在几何方面，它是全等三角形HL判定的关键依据，也是等腰三角形求高时极其重要的依据 ；在代数领域，它能够衔接一元二次方程来求解未知边长，并且还可以对 √2等无理数的几何意义作出解释 ；在坐标体系当中，两点间距离公式的本质实际上就是勾股定理的坐标呈现 。

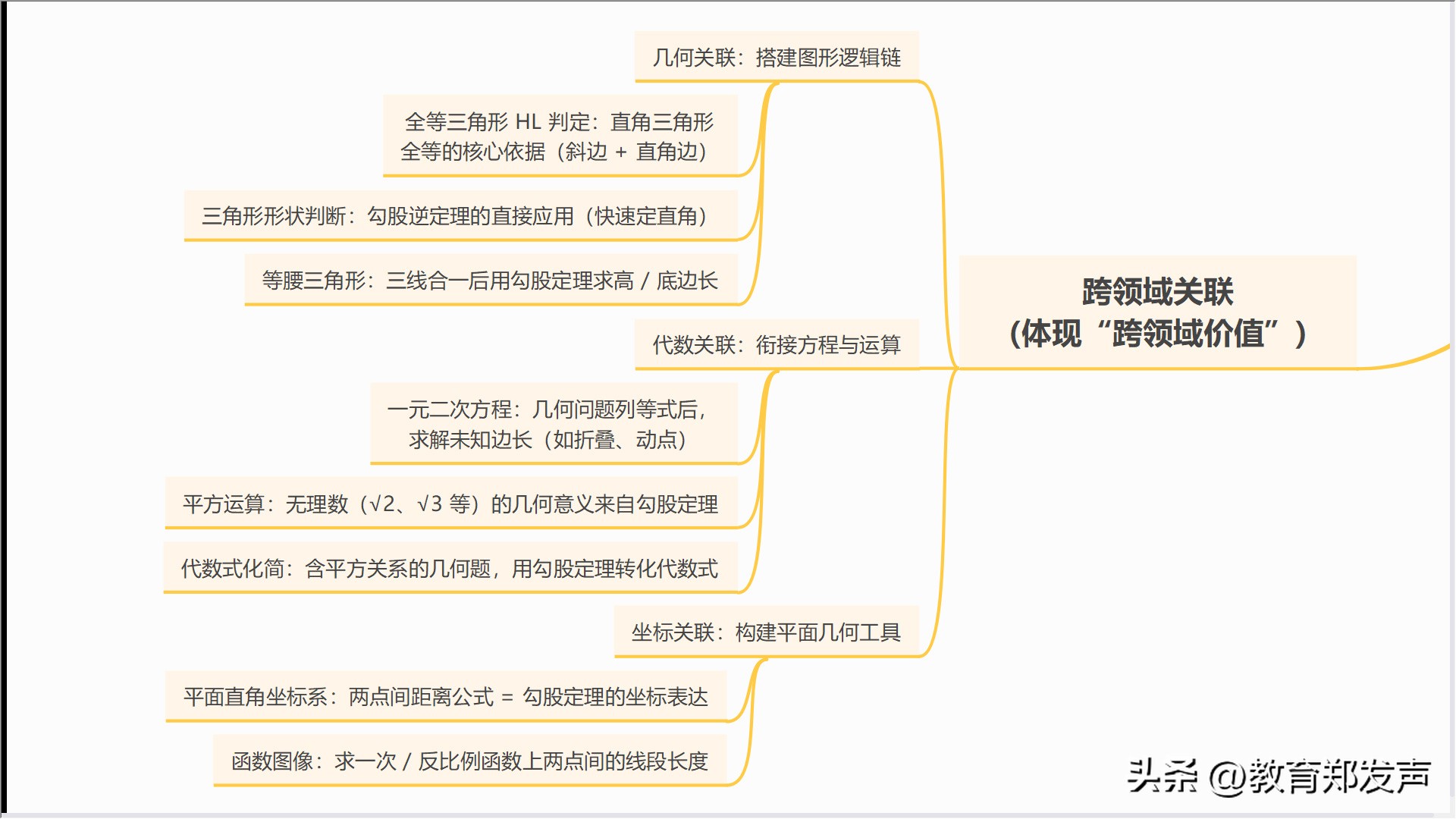
其所应用的场景更是将学习与生活都涵盖在内：在纯粹的几何环境当中pg下载麻将胡了安卓专属特惠.安卓应用版本.中国，能够对直角三角形计算、折叠以及动点等高频出现的考点予以解决；在生活范畴里，能够对河宽进行间接测量，对楼高进行测量，对航海方位作出判断，对建筑直角进行判定；在综合题型之中，是函数图像线段长度以及几何压轴题的核心运用工具。

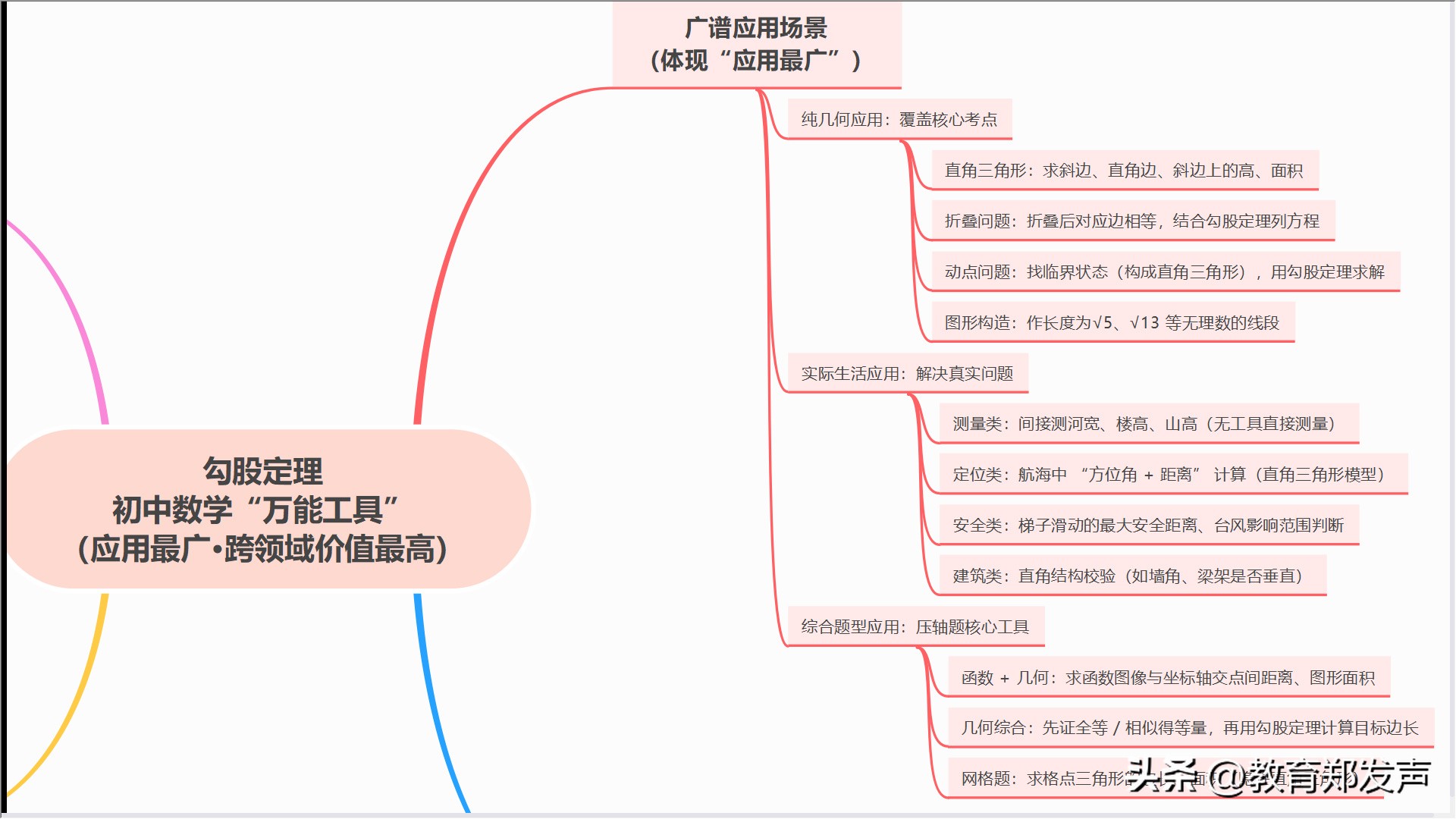
以“a²+b²=c²”的定义以及逆定理作为基础，从中拓展出来30°-60°-90°等特殊三角形边长比pg下载网站麻将胡了，还拓展出勾股数等实用内容，并构成完整知识链 。

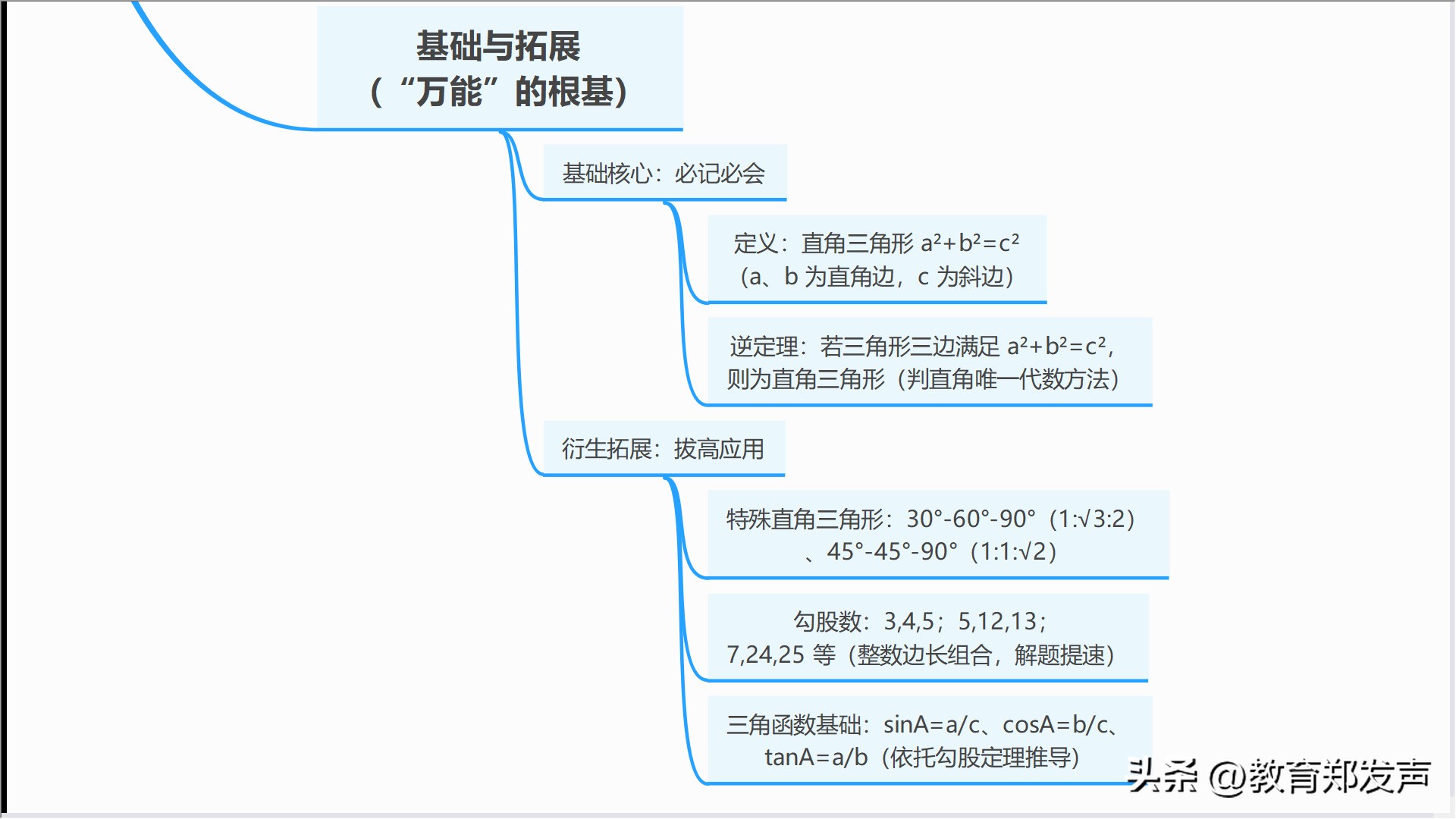
按照勾股定理学习逻辑，能提炼数学学习核心方法，其一，抓核心联分支，先弄明白的本质，再去延伸关联知识，这是一种方法；其二坚持数形彼此转换，把几何图形和代数里的运算进行相互转化，这是另一种方法；其三学以致用让落实到实际应用题和生活里的问题，这又是一种方法；其四注重前后衔接，明白知识递进关系为后续学习打基础，这是最后一点，把多种方法结合才能搭建起系统数学逻辑思维 。

今日所呈现的内容极为“干”，期望诸位能够认真地予以查看，着实是格外具有用途可言。进行一个关注以及转发的操作pg下载官方版打开即玩v1022.速装上线体验.中国，给予相应的予以支持 。