pg下载麻将胡了 平均薪资的陷阱和真相

2.2 平均薪资的陷阱和真相

公司平均薪资比较高，其待遇就必然会很好么，除了均值之外，还有别的啥统计量能用以反映样本数据的中心呢pg下载麻将胡了，去尾平均数以及加权平均数到底分别是什么呀。箱线图又为啥物呢，常用的统计量数量这般之多，到底哪一个统计量才算是最佳的那个统计量呢？

2.2.1 是谁拉高了平均薪资

小明这位拥有刚毕业身份状态的大学生，经历了层层面试环节，成功被一家公司录用，进而成为了一名工程师。这家具备环境优美、气氛融洽这一特点的公司中，唯一使得小明内心生出不满认知情绪的便是那份报酬薪资。在入职之前，老板宣称此公司里的整体薪酬平均数为数值10000元，然而小明所得的实际薪酬却仅仅为6000元。

并且，不光是小明的薪酬不高的薪酬没有，就连他的同事们所获取的薪资通常也只是 6000 元而已，距离老板表示的 10000 元薪资还差得远，小明带着不高兴的情绪去找了老板，老板满脸笑容地讲：“我可没骗你。在你没来以前公司里一共有 12 个人，我的薪资是 50000，两名主管的薪资是 10000，5 名工程师的薪资是 6000，还有 4 名工程师助理的薪资是 5000。你去算一算，这不刚好人均 10000 嘛。”表 2.1 所呈现的是 12 个员工的薪资分布情况。

表2.1 薪资分布

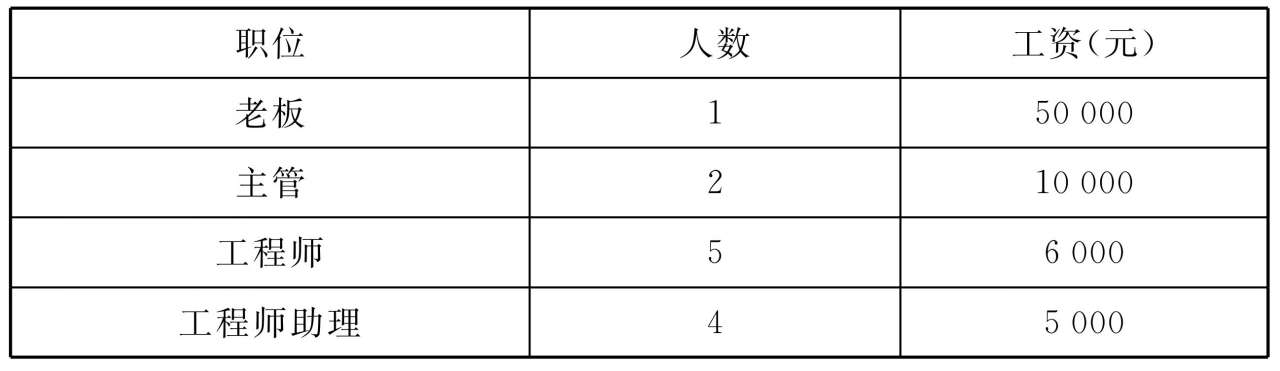
小明算了算，薪资均值为

果然，全体员工薪酬的均值恰好正是10000。小明难免不禁有些不太高兴，心里暗自这样想着：当初倘若曾经去问老板薪资的中位数究竟是多少那该多好啊。 ”。

公司之中存在十二个人，其工资依据从高而低的顺序排列，依次分别是五万、一万、一万、六千、六千、六千、六千、六千、五千、五千、五千、五千 ；公司里的薪资中位数所指的乃是第六个人的与第七个人的薪资二者的均值；经过排序第六的薪资是六千并且第八的薪资同样是六千；公司里职员薪资的中位数也便是六千；此六千刚好相等于是小明的收入 。

有一张图，它是图2.1，这张图画出了那12个员工薪资的分布直方图。在这12个员工里，有11个人的薪资集中在5000至10000这个范围，但是呢，只有老板的薪资是大于10000的。员工薪资的中位数能够比较好地反映大部分人力的薪资水平，然而呢，均值明显要大于中位数。这是因为老板的薪资过高，进而拉高了均值水准。结果就是这样啦。

图2.1 薪资分布直方图

呈现数据中心的均值与中位数，能体现出样本数据总是围绕在它们附近，不过与更加安定不受极端值干扰的中位数相比较而言，均值是更容易遭受极端值影响的那种数据统计量，比方来说，在上述所举例子当中，老板不菲的薪资就对均值造成了严重的影响 。

一组数据的均值假如远超中位数，那就表明该组数据里存在极大的异常值，反之亦然；一组数据的均值要是远小于中位数，这就意味着此处数据存在极小的异常值，反过来也是如此；一组数据的均值倘若与中位数极为相近，或许是该组数据不存在异常值，也有可能是数据里同时有极大的异常值和极小的异常值，二者对均值的影响彼此抵消，反过来同样成立 。

在考量数据中心所作相关度量的时候，中位数展现出的稳定性相较于均值而言是来得更好的，然而均值反倒要比中位数在大众心里更具备被接受的程度。可通过使用去尾均值来替换均值的方式，也就是做移除那些存在样本里的最大值以及最小值的事儿之后，接着对最终获得的结果去予以均值的计算，以此来达成想要达到增加均值稳定性这方面的目的；在歌手进行赛事比赛那种场景之下，不时能看到会有将最高的评委所做出的打分予以除去的情况，而后随后会去把几个评委进行评分这件事后所得到计算出来的均值当作歌手的得分，这样的情况就是去尾均值在实际当中的一处具体应用实例存在的体现 。

2.2.2 如何计算加权平均薪资

次一年的那毕业季时辰，有个学弟寻到了小明，说道：“学长呀，听闻你们公司薪资待遇那可是相当不错呢，平均工资几乎快要接近10000啦，这是真如此的状况吗？你们公司当中一共是存有几种薪酬层面所对应的水平情形呀？”。

于过去的一整年当中，小明所处公司的人事状况未曾出现变动，每一个人的薪资情况同样没有出现变动，仅仅是小明予以加入之后，公司的总体人员数量变成了十三人，就如同表二点二所呈现的那样。

表2.2 小明加入公司后的薪资分布

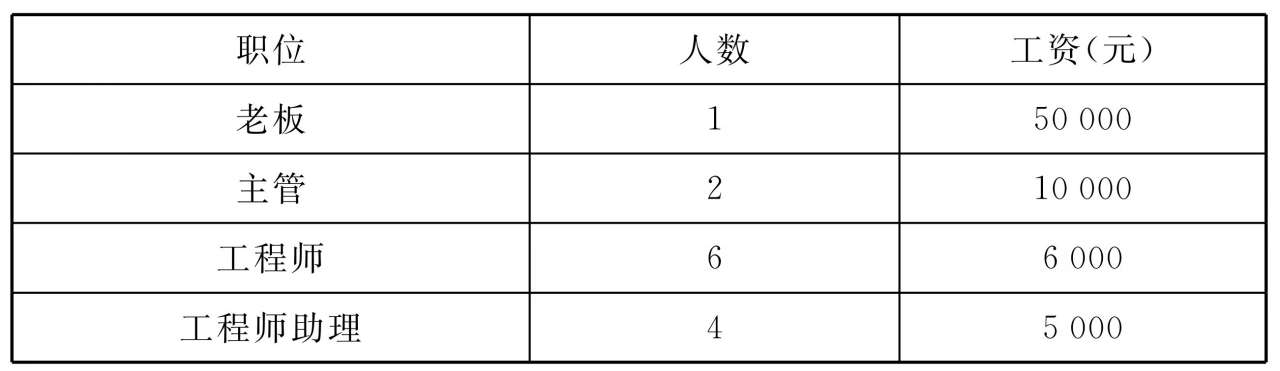
小明进行了相关计算，得出在他自己加入到该公司后，这家公司之中全体员工的薪资均值大概是7538元，而其有着相应的计算公式，是这样的 。

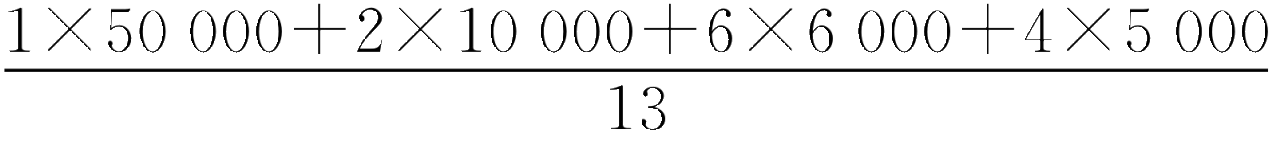
将公司人员数量设定为单位“一”且为十三人，其工资依据从高朝着低进行排列，顺序依次涵盖金额五万、数字一万、一万之整数，六千之数、六千、六千、同一六千若干、第五数个相同者六千、六千最后者、中间呈现单位数之五千、再有五千多个、五千又若干、终了为五千之数。员工薪资所处居中之数变为在排序当中位列第七的报酬金额单位，此单位恰好是六千之数元整。

小明赶忙回应学弟：“我所在公司依照平均算薪资大概达到7500元，然而从薪资顺序位置处于中间量来作比较的那个数只有6000元，当中薪酬所处水准总共存在4个等级。老板所获取拿到手的为50000元，部门管理者所领取收取的是10‍000元，从事工程技术工作的人员手头所拥有的是6000元，协助做些底层工程技术相应辅助之工作的人员具备着5000元。”。

学弟追问道：“那众数呢？”

众数是什么呐，它指的乃样本数据里出现次数最多的数据。在这例证当中，存在这样一种状况，有6个人的工资数额为6000元，所以呢，由此可推出员工薪酬的众数便是6000。对于一组数据而言呀哈，其中的众数并非仅仅只有一个哦，它是有可能存在好几个的哟。假设说最初的时候呀，小明所担任的职位并非是工程师，而是工程师助理，那么在公司如此这般的薪酬分布情形下，工程师和工程师助理这两类职位的人数就会各自出现5个这种数量相对均衡的状况，如此一来便会出现这样的结果啦，员工薪酬的众数就会变成有两个pg下载，其中一个是6000，另外一个则是5000。

小明回答说：“众数也是6000。”

学弟经过一番思考后，作出决定准备算一算加权平均薪资，学弟并不晓得公司里每一种职位究竟有多少人在供职。他凭借自身成绩以及面试时期的表现对自己拿到每一类职位的概率进行了估计，4种职位的就职概率如呈于表表 2.3 所示。

表2.3 4种职位的就职概率

学弟觉得自己没可能变成老板，成为主管的可能性是百分之二十，成为工程师的可能性是百分之五十，成为工程师助理的可能性是百分之三十。把各类职位的就职可能性当成权重，进而加权后的平均薪资乃是五万乘以百分之零，加上一万乘以百分之二十，加上六千乘以百分之五十，加上五千乘以百分之三十，也就是六千五百元 。

存在一种平均数的变形，它被称作加权平均数。小明所算出的平均数，同样能够当作一种加权平均数去看待，这类加权平均数的权重，乃是按照每种职位上的供职人数比例而定的。

均值呀他可以反映数据中心，中位数呢也能反映数据那个中心部分，众数呢同样可把起到反映作用，加权均值这一项同样能够针对数据显示出它那个中心状况咧，就在这个例子当中哟，这学弟没办法知晓到每种任职位置上面供职人们的数量状况呢，与此同时哦学弟还觉着自己得以获取每种职位这种的概率它并非是一致的时候的啦，这样来讲因而呀是特别有必要对那个加权均值进行计算一番的呀。

当样本已然分组，或者样本之间重要程度并非一致之时，加权均值方才适用。举例而言，在开展经济发展指标计算工作之际，鉴于大企业对经济所具备的影响力远远超过小企业这种状况，所以呀，在依据企业利润率来计算经济发展指标的这一过程当中，就得赋予大企业一较大的权重，以此来彰显其较为强劲的影响力。

2.2.3 用四分位数估计薪资区间

存有除加权平均数之外其他常用的数值平均数，这些平均数涵盖调和平均数跟几何平均数之类别 它们是分别适用于几种不同的情况的平均数值，这些平均数值表达了数据的中心 。

有另外一种在数据当中可以用来体现其分布样式的统计方面的量，它被称作四分位数。把所有样本点所处的区间当作是一条数轴，中位数所针对那种处于整体位置百分之五十地方的数，而四分位数所涉及的就是处在整体位置百分之二十五处以及百分之七十五之处两种位置的数。

小明所在公司里有十三个人，他们工资按照从高至低的顺序排列分别是五万、一万、一万、六千、六千、六千、六千、六千、六千、五千、五千、五千、五千 。处于百分之二十五位置的数是排序第四的那个数，也就是六千；处于百分之七十五位置的数是排序第十的那个数pg下载，也就是五千 。两个四分位数和中位数恰好能够把数据均匀地分成四份 。

此外呀，在小明所在公司之内，薪资方面，最高水准的金额为50000，最低程度的数额是5000，处于中间位置的薪资额度是6000，这三个用来统计的数据，加之两个四分位数组合在一起，就能够制作成一个箱线图，也就是被标示为（见图2.2）的那种图表啦。

图2.2 小明所在公司的薪酬箱线图

箱线图由5根横线构成，在最上方的，是处于极大值位置的一根短线，其下方，是处于上四分位数那里的一根长线，再往下，是处于中位数位置的一根长线，继续向下，是处于下四分位数位置的一根长线，最下方的，是处于极小值位置的一根短线，其中，3根长线共同组成一个呈“日”字形的箱子，而位于两端的两根短线，是通过虚线与中间的箱子连接起来的。

在图2.2之中，鉴于上四分位数跟中位数二者相同，并且下四分位数与极小值二者相同，所以造就了一个处于下方被压扁的箱子，唯有老板的薪资高高地悬挂于最上方。为方便明白理解意思，图2.3是一张具备更普遍意义情形的箱线图。

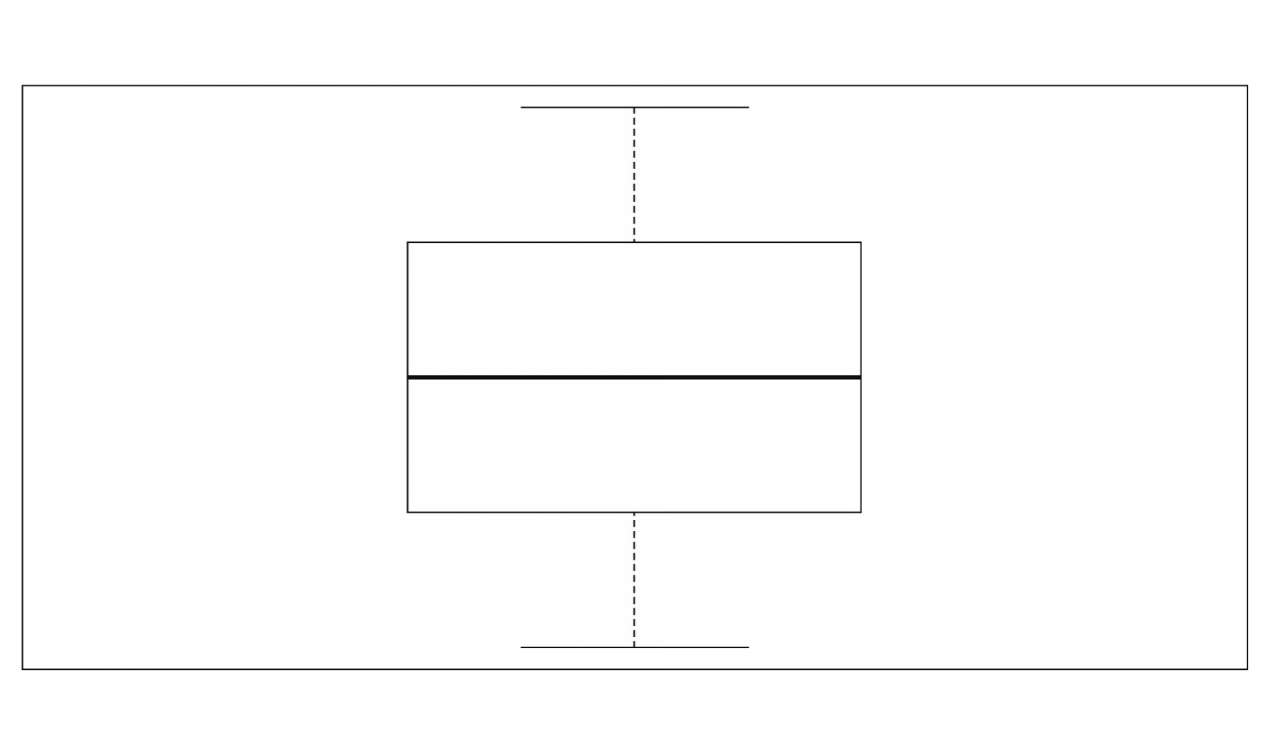
图2.3 数据分布十分均匀的箱线图

图2.3呈现的乃是一张相当标准的箱线图，有关的样本数据极为均衡，正好有一半的数据聚集于那上下四分位数之间，另有1/4的数据排列于最大值与较大四分位数区间，并且1/4的数据分布于最小值与较小四分位数所规定的范围。

将图2.2于相较中的图2.3之下，其形状可谓诡秘奇怪令人难于言表其样态。被大力按压至极为扁样的匣子给予人的知晓条件是得出了五千元至六千元额度的三千人中占有了四倍人中三倍人群的薪资所在范围界限。对于学弟来论言说这事，只要是将目光落于图2.2之上，就能够推测预估出自身薪资也会处于五千元至六千元这个区间范围之内。

较为全面地反映出样本数据之中的信息的是箱线图 ，当样本的个数比较多的时候 ，箱线图显得格外有用 。然而箱线图仅仅适用于数值型数据 ，对于分类数据和顺序数据来说 ，绘制箱线图均没有意义 。除箱线图之外 ，像均值 、加权均值 、去尾均值这类情况也是这样 ，仅仅适用于数值型数据 。

统观上述诸多统计数据，学弟便能够预先知晓他工资待遇范围会置身于5000至6000元之间，这会助力他去判定可否踏入小明所在的那家公司。总体而言，这些统计数据各有各的长处，均值适用范畴更加宽泛，中位数更为精准。于解决实际问题之际，从多种角度考量这些统计数据，让它们所呈现的信息彼此相互印证，这才是更为妥善的抉择。