pg下载麻将胡了A.旗舰厅进体育.cc 斐波那契数列-高中数学重要命题背景第12集

被称作“比萨的莱昂纳多”的意大利数学家莱昂纳多·斐波那契（Leonardo Fibonacci），是斐波那契数列的定义者，他生于公元1170年，卒于1250年，籍贯是比萨，在1202年撰写了《算盘全书》（Liber Abacci）一书，他还是第一个研究印度和阿拉伯数学理论的欧洲人。他的父亲受比萨的一家商业团体聘请，担任外交领事，派驻于阿尔及利亚地区，莱昂纳多借此在一位阿拉伯老师的指导下钻研数学，他也曾在埃及、叙利亚、希腊、西西里和普罗旺斯等地开展数学研究，此外斐波纳契还在计算机C语言程序题里有着广泛应用。

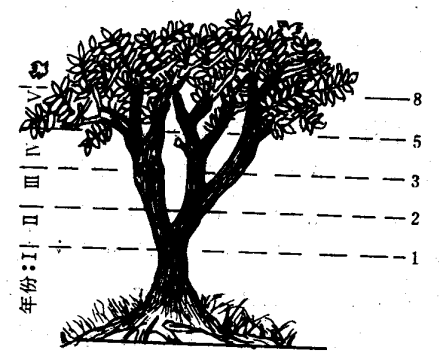
在自然科学的其他分支当中，斐波那契数列存在着诸多应用，如在树木生长方面，新生的枝条常常需要一段用于自身生长的“休息”时间，之后才能够萌发新枝，所以一株树苗在某个间隔，像一年这样，之后会长出一条新枝，第二年新枝处于“休息”状态，老枝依旧会萌发，此后老枝与经过一年“休息”的枝会同时萌发pg下载，当年生长的新枝则会在次年“休息”，如此一来，一株树木各个年份的枝桠数便形成了斐波波那数列，而这个规律就是生物学领域所著名的“鲁德维格定律” 。

此外，去观察延龄草的花瓣，再观察野玫瑰的花瓣，接着观察南美血根草的花瓣，然后观察大波斯菊的花瓣，随后观察金凤花的花瓣，再接着观察耧斗菜的花瓣pg下载通道，之后观察百合花的花瓣，最后观察蝴蝶花的花瓣，能够发觉它们花瓣的数目呈现出斐波那契数：3、5、8、13、21……

花瓣数目方面存在不同情况，其中的百合花则是 3 瓣，梅花是 5 瓣，飞燕草呢为 8 瓣，万寿菊是 13 瓣，向日葵有 21 瓣或者 34 瓣这两种情况，雏菊有 34 瓣，雏菊有 55 瓣，雏菊还有 89 瓣这三个不同的花瓣数目情况。

蓟的头部，有着斐波那契螺旋，其中存在 13 条螺旋是顺时针旋转的，同时还有 21 条螺旋是逆时针旋转的。

这些植物，是依照自然规律，演变至此的。这好像是植物排列种子的“优化途径”，这般能让所有种子有着近乎相同的大小，且疏密适宜，不会在圆心位置挤入过多种子，而在圆周位置又显得稀疏零落。叶子的生长方式是这样，对好多植物而言pg下载，一片片叶子从靠近中轴线的地方长出来 ，在生长进程里要始终能最好地利用空间 ，鉴于叶子是一片一片慢慢长出来的 ，并非一下子同时出现，每片叶子和前一片叶子间形成的角度应当是222.5° ，这个角度被称作“黄金角度” ，因其同整个圆周360°的比值 ，是黄金分割数0.618033989……的倒数 ，有了这种特殊角度的生长方式 ，就致使斐波那契螺旋得以产生 。向日葵种子排列所形成的斐波那契螺旋，有时数目能达到89条，甚至还会有144条。1992年的时候，两位来自法国的科学家，通过针对花瓣形成过程展开的计算机仿真实验，证实了在系统维持最低能量的状态之时，花朵会按照斐波那契数列逐渐长出花瓣。

首先，斐波那契弧线被称作斐波那契扇形线。其次，其趋势线的绘制是以两个端点为依据的，举例来说，是从最低点反向指向最高点这条线的，如同上面的两个点。接着，要通过第二个点，去画出这样一条线，这时候会画出一种情况，就是“无形的（看不见的）”垂直线处于那儿。随后，从第一个点开始，要绘制第三条趋势线，这条趋势线会出现三种程度百分比下的交叉情况，它们分别是38.2%，50%以及61.8%的无形垂直线被交叉。

斐波纳契弧线为潜在的支持点以及阻力点水平价格，此点与斐波纳契扇形线往往会在图表里同时被绘画出来，而支持点和阻力点正是透过这些线的交汇点得到的 。

需要留意的是，弧线的交叉点会变动，价格曲线也会因图表数值范围而变化，由于弧线属于圆周的一部分，其形成一直是相同的。

斐波那契有很多性质，我们例举出常用的性质：

既然斐波那契数列乃这般重要的数列，于高考里的现身也就极为频繁，且具重要性。好多考试未能真正得分的主要缘由在于针对斐波那契数列及其性质掌握得不够稳固，或是一知半解因而造成的情况所致。 。

下面我们对斐波那契数列及其例题做简要解答，供同学们参考。

有兴趣的同学不妨做一做，更多问题，欢迎留言交流