30度60度90度勾股定理是什么
勾股定理，作为几何学中的基础理论，阐述了直角三角形的两条直角边平方之和等于斜边平方的规律。在我国，人们将直角三角形称作勾股形，其中较短的直角边被称为勾，较长的直角边称为股，而斜边则被称作弦。因此，这个定理被命名为勾股定理，亦有人称之为商高定理。
勾股定理的证明方式已达到约500种开yunapp体育官网入口下载...
生活应用 第173页
郑州地铁云购票app
郑州轨道交通官方精心打造了这款名为“郑州地铁云购票”的应用程序开元棋官方正版下载，旨在为用户提供一种便捷的在线购票方式。该应用不仅具备快速购票的实用功能，还支持用户实时查询地铁站点及列车到站时间等信息。若您有购票需求，不妨前往IT猫扑平台下载体验。
软件介绍
为了便于民众乘坐地铁，郑州地铁公司充分利用移动互联...
什么是牛顿第二运动定律？
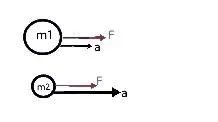
牛顿第二定律阐述了物体的加速度与施加于其上的力成正比，同时与物体的质量成反比关系。此外，该定律还指出，加速度的指向与施加力的方向一致。
用公式可以表示为：a=F净/m。其中：
a——加速度，
F净——作用在物体上的总力或净力，
m——物体的质量。
牛顿第一定律与第二定律共同构成了对力与物体运动之间相互作用的更...
关于勾股定理的小故事
我国西汉时期著名的数学典籍《周髀算经》中记载了商高与周公的对话。周公向商高提问：“天无法用阶梯攀登，地也无法用寸尺测量至尽头。”那么，天的高度以及地面测量的数据是如何得出的呢？
商高说：“故折矩以为勾广三，股修四，经隅五。”
在中国古代，人们将手臂弯曲成直角时，其上臂部分称作“勾”，下臂部分称作“股”。商高在...
大自然的隐秘技能：神奇的Fibonacci数列
科学也跨界，它总以意想不到的方式，无处不在。
在这看似单调的数列背后，蕴藏着令人惊叹的科学魅力。您若不信，不妨跟随中国科学院物理研究所的曹则贤老师，一同探寻斐波那契数列那神奇而迷人的变化过程。
自然数的数量是无限的。当我们依照某种规则将这些数字依次排列时，便形成了一个序列。这个序列可以用函数的形式来表示，即...
分享一个神奇的操作系统——斐波那契+MACD，每一波都有20%以上的收益！
斐波那契数列，亦称兔子数列或黄金分割数列，它是一个特定的数列，其定义如下：
从第三个数开始，每个数都是它前两个数的总和开yun体育官网入口登录app，如0、1、1、2、3、5、8、13、21……。
为何称之为兔子数列呢？我们设想，兔子在满两个月后便具备了生育的能力，每对兔子每月都能产下一对幼兔。起初开元ky8...
卷积（背后意义、应用及计算）
一、卷积及其背后的意义
卷积的意义在于：在上一节中，我们讨论了傅里叶变换，其目的在于将一个函数分解为若干个不同频率的正弦波组成。那么，为何要将一个完整的函数分解为正弦波呢？这是因为这样做可以简化计算过程。正弦函数在求导和积分后，其结果依然是正弦函数，同时，许多在时域难以处理的问题，在频域中却变得简单易解，例如...
牛顿力学在生活中的应用
牛顿力学在生活中的应用
《牛顿力学在生活中的无处不在》
你是否曾思考过，在公园里悠然自得地摇曳秋千，亦或是稳如泰山地驾驭着单车，
在那些伟大的发明和发现背后，往往有一位杰出的科学家在默默贡献着智慧。没错，正是牛顿。
力学领域。牛顿的力学理论宛如一把开启奥秘的钥匙，为我们揭示了生活中众多现象的深层原理，极大地丰...
卷积神经网络——为什么卷积哪儿都能用？
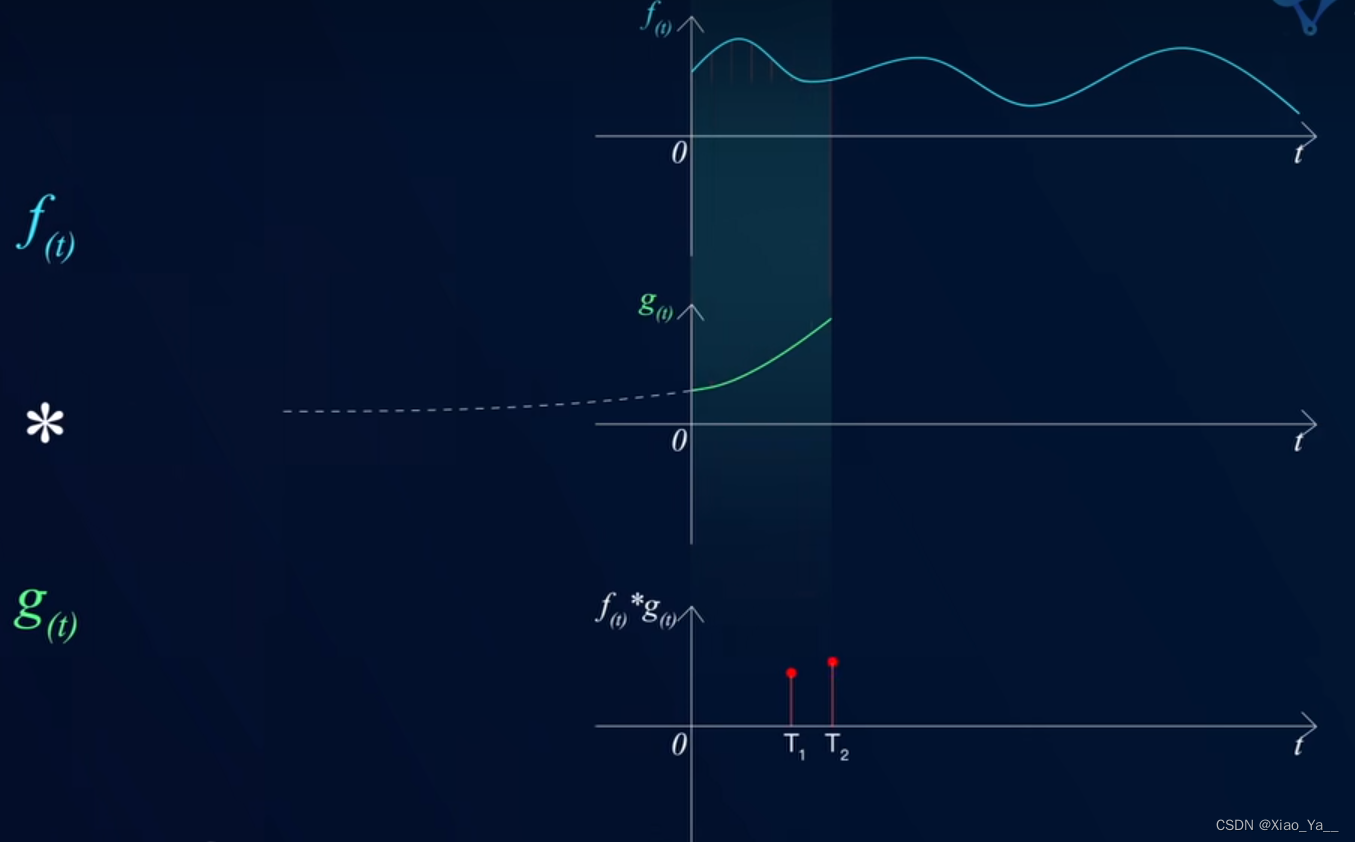
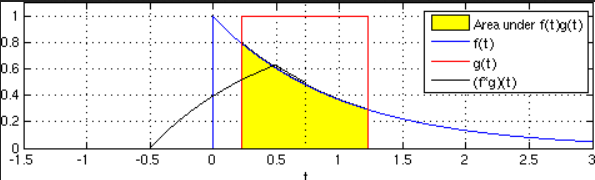
两个函数的卷积
本质上就是先将一个函数翻转，然后进行滑动叠加。
在连续情况下，叠加指的是对两个函数的乘积求积分。
在离散情况下就是加权求和。
它在不同的领域有着不同的解释
在热力系统领域，卷积运算常被应用于对连续加入的燃料在燃烧过程中所释放出的整体热能进行计算。
在信号处理领域，卷积运算被广泛运用，用...
